On the Convergence and Stability of Upside-Down Reinforcement Learning, Goal-Conditioned Supervised Learning, and Online Decision Transformers

This article provides a rigorous analysis of convergence and stability of Episodic Upside-Down Reinforcement Learning, Goal-Conditioned Supervised Learning and Online Decision Transformers. These algorithms performed competitively across various benchmarks, from games to robotic tasks, but their theoretical understanding is limited to specific environmental conditions. This work initiates a theoretical foundation for algorithms that build on the broad paradigm of approaching reinforcement learning through supervised learning or sequence modeling. At the core of this investigation lies the analysis of conditions on the underlying environment, under which the algorithms can identify optimal solutions. We also assess whether emerging solutions remain stable in situations where the environment is subject to tiny levels of noise. Specifically, we study the continuity and asymptotic convergence of command-conditioned policies, values and the goal-reaching objective depending on the transition kernel of the underlying Markov Decision Process. We demonstrate that near-optimal behavior is achieved if the transition kernel is located in a sufficiently small neighborhood of a deterministic kernel. The mentioned quantities are continuous (with respect to a specific topology) at deterministic kernels, both asymptotically and after a finite number of learning cycles. The developed methods allow us to present the first explicit estimates on the convergence and stability of policies and values in terms of the underlying transition kernels. On the theoretical side we introduce a number of new concepts to reinforcement learning, like working in segment spaces, studying continuity in quotient topologies and the application of the fixed-point theory of dynamical systems. The theoretical study is accompanied by a detailed investigation of example environments and numerical experiments.

Hierarchical Multi-Agent Reinforcement Learning for Air Combat Maneuvering

The application of artificial intelligence to simulate air-to-air combat scenarios is attracting increasing attention. To date the high-dimensional state and action spaces, the high complexity of situation information (such as imperfect and filtered information, stochasticity, incomplete knowledge about mission targets) and the nonlinear flight dynamics pose significant challenges for accurate air combat decision-making. These challenges are exacerbated when multiple heterogeneous agents are involved. We propose a hierarchical multi-agent reinforcement learning framework for air-to-air combat with multiple heterogeneous agents. In our framework, the decision-making process is divided into two stages of abstraction, where heterogeneous low-level policies control the action of individual units, and a high-level commander policy issues macro commands given the overall mission targets. Low-level policies are trained for accurate unit combat control. Their training is organized in a learning curriculum with increasingly complex training scenarios and league-based self-play. The commander policy is trained on mission targets given pre-trained low-level policies. The empirical validation advocates the advantages of our design choices.

Hedging of Financial Derivative Contracts via Monte Carlo Tree Search

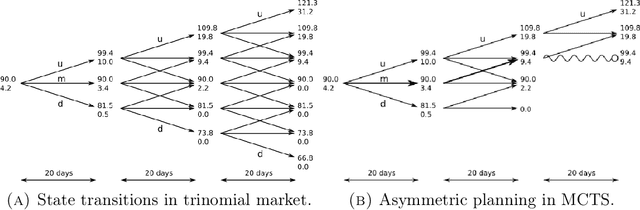
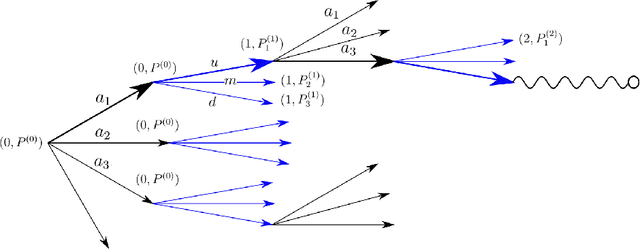
The construction of approximate replication strategies for derivative contracts in incomplete markets is a key problem of financial engineering. Recently Reinforcement Learning algorithms for pricing and hedging under realistic market conditions have attracted significant interest. While financial research mostly focused on variations of $Q$-learning, in Artificial Intelligence Monte Carlo Tree Search is the recognized state-of-the-art method for various planning problems, such as the games of Hex, Chess, Go,... This article introduces Monte Carlo Tree Search as a method to solve the stochastic optimal control problem underlying the pricing and hedging of financial derivatives. As compared to $Q$-learning it combines reinforcement learning with tree search techniques. As a consequence Monte Carlo Tree Search has higher sample efficiency, is less prone to over-fitting to specific market models and generally learns stronger policies faster. In our experiments we find that Monte Carlo Tree Search, being the world-champion in games like Chess and Go, is easily capable of directly maximizing the utility of investor's terminal wealth without an intermediate mathematical theory.

An exact kernel framework for spatio-temporal dynamics

A kernel-based framework for spatio-temporal data analysis is introduced that applies in situations when the underlying system dynamics are governed by a dynamic equation. The key ingredient is a representer theorem that involves time-dependent kernels. Such kernels occur commonly in the expansion of solutions of partial differential equations. The representer theorem is applied to find among all solutions of a dynamic equation the one that minimizes the error with given spatio-temporal samples. This is motivated by the fact that very often a differential equation is given a priori (e.g.~by the laws of physics) and a practitioner seeks the best solution that is compatible with her noisy measurements. Our guiding example is the Fokker-Planck equation, which describes the evolution of density in stochastic diffusion processes. A regression and density estimation framework is introduced for spatio-temporal modeling under Fokker-Planck dynamics with initial and boundary conditions.

Hedging using reinforcement learning: Contextual $k$-Armed Bandit versus $Q$-learning

The construction of replication strategies for contingent claims in the presence of risk and market friction is a key problem of financial engineering. In real markets, continuous replication, such as in the model of Black, Scholes and Merton, is not only unrealistic but it is also undesirable due to high transaction costs. Over the last decades stochastic optimal-control methods have been developed to balance between effective replication and losses. More recently, with the rise of artificial intelligence, temporal-difference Reinforcement Learning, in particular variations of $Q$-learning in conjunction with Deep Neural Networks, have attracted significant interest. From a practical point of view, however, such methods are often relatively sample inefficient, hard to train and lack performance guarantees. This motivates the investigation of a stable benchmark algorithm for hedging. In this article, the hedging problem is viewed as an instance of a risk-averse contextual $k$-armed bandit problem, for which a large body of theoretical results and well-studied algorithms are available. We find that the $k$-armed bandit model naturally fits to the $P\&L$ formulation of hedging, providing for a more accurate and sample efficient approach than $Q$-learning and reducing to the Black-Scholes model in the absence of transaction costs and risks.