Gradient-based bilevel optimization for multi-penalty Ridge regression through matrix differential calculus

Common regularization algorithms for linear regression, such as LASSO and Ridge regression, rely on a regularization hyperparameter that balances the tradeoff between minimizing the fitting error and the norm of the learned model coefficients. As this hyperparameter is scalar, it can be easily selected via random or grid search optimizing a cross-validation criterion. However, using a scalar hyperparameter limits the algorithm's flexibility and potential for better generalization. In this paper, we address the problem of linear regression with l2-regularization, where a different regularization hyperparameter is associated with each input variable. We optimize these hyperparameters using a gradient-based approach, wherein the gradient of a cross-validation criterion with respect to the regularization hyperparameters is computed analytically through matrix differential calculus. Additionally, we introduce two strategies tailored for sparse model learning problems aiming at reducing the risk of overfitting to the validation data. Numerical examples demonstrate that our multi-hyperparameter regularization approach outperforms LASSO, Ridge, and Elastic Net regression. Moreover, the analytical computation of the gradient proves to be more efficient in terms of computational time compared to automatic differentiation, especially when handling a large number of input variables. Application to the identification of over-parameterized Linear Parameter-Varying models is also presented.

Split-Boost Neural Networks

The calibration and training of a neural network is a complex and time-consuming procedure that requires significant computational resources to achieve satisfactory results. Key obstacles are a large number of hyperparameters to select and the onset of overfitting in the face of a small amount of data. In this framework, we propose an innovative training strategy for feed-forward architectures - called split-boost - that improves performance and automatically includes a regularizing behaviour without modeling it explicitly. Such a novel approach ultimately allows us to avoid explicitly modeling the regularization term, decreasing the total number of hyperparameters and speeding up the tuning phase. The proposed strategy is tested on a real-world (anonymized) dataset within a benchmark medical insurance design problem.

Hedging using reinforcement learning: Contextual $k$-Armed Bandit versus $Q$-learning

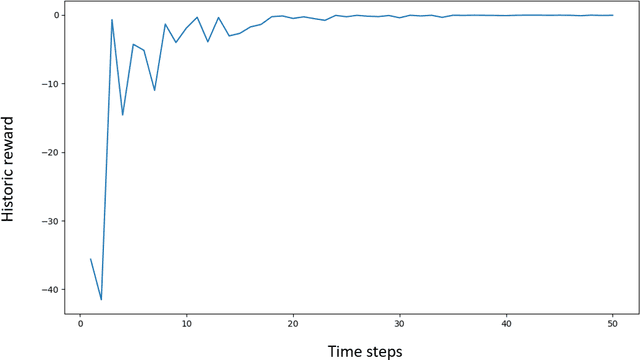
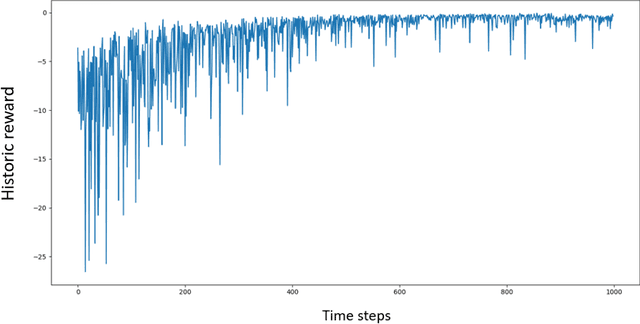
The construction of replication strategies for contingent claims in the presence of risk and market friction is a key problem of financial engineering. In real markets, continuous replication, such as in the model of Black, Scholes and Merton, is not only unrealistic but it is also undesirable due to high transaction costs. Over the last decades stochastic optimal-control methods have been developed to balance between effective replication and losses. More recently, with the rise of artificial intelligence, temporal-difference Reinforcement Learning, in particular variations of $Q$-learning in conjunction with Deep Neural Networks, have attracted significant interest. From a practical point of view, however, such methods are often relatively sample inefficient, hard to train and lack performance guarantees. This motivates the investigation of a stable benchmark algorithm for hedging. In this article, the hedging problem is viewed as an instance of a risk-averse contextual $k$-armed bandit problem, for which a large body of theoretical results and well-studied algorithms are available. We find that the $k$-armed bandit model naturally fits to the $P\&L$ formulation of hedging, providing for a more accurate and sample efficient approach than $Q$-learning and reducing to the Black-Scholes model in the absence of transaction costs and risks.