Giuseppe Nuti
Deep Hedging Under Non-Convexity: Limitations and a Case for AlphaZero
Oct 02, 2025



Abstract:This paper examines replication portfolio construction in incomplete markets - a key problem in financial engineering with applications in pricing, hedging, balance sheet management, and energy storage planning. We model this as a two-player game between an investor and the market, where the investor makes strategic bets on future states while the market reveals outcomes. Inspired by the success of Monte Carlo Tree Search in stochastic games, we introduce an AlphaZero-based system and compare its performance to deep hedging - a widely used industry method based on gradient descent. Through theoretical analysis and experiments, we show that deep hedging struggles in environments where the $Q$-function is not subject to convexity constraints - such as those involving non-convex transaction costs, capital constraints, or regulatory limitations - converging to local optima. We construct specific market environments to highlight these limitations and demonstrate that AlphaZero consistently finds near-optimal replication strategies. On the theoretical side, we establish a connection between deep hedging and convex optimization, suggesting that its effectiveness is contingent on convexity assumptions. Our experiments further suggest that AlphaZero is more sample-efficient - an important advantage in data-scarce, overfitting-prone derivative markets.
Mixture of Raytraced Experts
Jul 16, 2025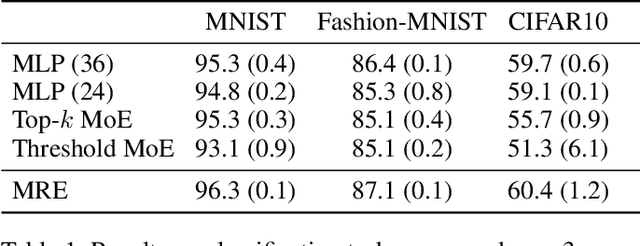
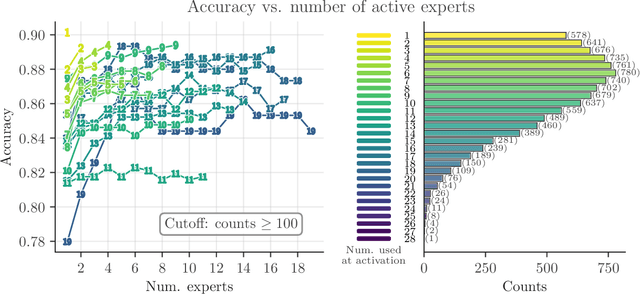
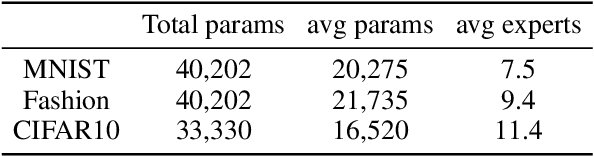
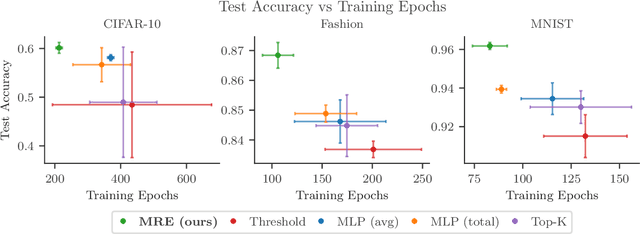
Abstract:We introduce a Mixture of Raytraced Experts, a stacked Mixture of Experts (MoE) architecture which can dynamically select sequences of experts, producing computational graphs of variable width and depth. Existing MoE architectures generally require a fixed amount of computation for a given sample. Our approach, in contrast, yields predictions with increasing accuracy as the computation cycles through the experts' sequence. We train our model by iteratively sampling from a set of candidate experts, unfolding the sequence akin to how Recurrent Neural Networks are trained. Our method does not require load-balancing mechanisms, and preliminary experiments show a reduction in training epochs of 10\% to 40\% with a comparable/higher accuracy. These results point to new research directions in the field of MoEs, allowing the design of potentially faster and more expressive models. The code is available at https://github.com/nutig/RayTracing
Ray-Tracing for Conditionally Activated Neural Networks
Feb 20, 2025


Abstract:In this paper, we introduce a novel architecture for conditionally activated neural networks combining a hierarchical construction of multiple Mixture of Experts (MoEs) layers with a sampling mechanism that progressively converges to an optimized configuration of expert activation. This methodology enables the dynamic unfolding of the network's architecture, facilitating efficient path-specific training. Experimental results demonstrate that this approach achieves competitive accuracy compared to conventional baselines while significantly reducing the parameter count required for inference. Notably, this parameter reduction correlates with the complexity of the input patterns, a property naturally emerging from the network's operational dynamics without necessitating explicit auxiliary penalty functions.
Hedging using reinforcement learning: Contextual $k$-Armed Bandit versus $Q$-learning
Jul 03, 2020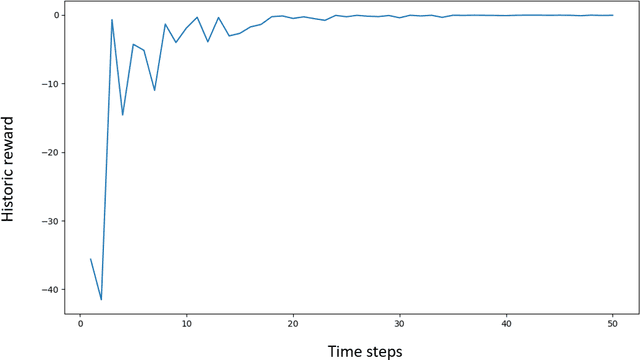


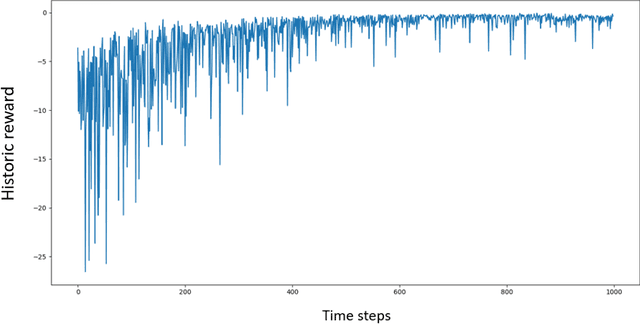
Abstract:The construction of replication strategies for contingent claims in the presence of risk and market friction is a key problem of financial engineering. In real markets, continuous replication, such as in the model of Black, Scholes and Merton, is not only unrealistic but it is also undesirable due to high transaction costs. Over the last decades stochastic optimal-control methods have been developed to balance between effective replication and losses. More recently, with the rise of artificial intelligence, temporal-difference Reinforcement Learning, in particular variations of $Q$-learning in conjunction with Deep Neural Networks, have attracted significant interest. From a practical point of view, however, such methods are often relatively sample inefficient, hard to train and lack performance guarantees. This motivates the investigation of a stable benchmark algorithm for hedging. In this article, the hedging problem is viewed as an instance of a risk-averse contextual $k$-armed bandit problem, for which a large body of theoretical results and well-studied algorithms are available. We find that the $k$-armed bandit model naturally fits to the $P\&L$ formulation of hedging, providing for a more accurate and sample efficient approach than $Q$-learning and reducing to the Black-Scholes model in the absence of transaction costs and risks.
Adaptive Bayesian Reticulum
Jan 29, 2020



Abstract:Neural Networks and Random Forests: two popular techniques for supervised learning that are seemingly disconnected in their formulation and optimization method, have recently been linked in a single construct. The connection pivots on assembling an artificial Neural Network with nodes that allow for a gate-like function to mimic a tree split, optimized using the standard approach of recursively applying the chain rule to update its parameters. Yet two main challenges have impeded wide use of this hybrid approach: \emph{(a)} the inability of global gradient descent techniques to optimize hierarchical parameters (as introduced by the gate function); and \emph{(b)} the construction of the tree structure, which has relied on standard decision tree algorithms to learn the network topology or incrementally (and heuristically) searching the space at random. We propose a probabilistic construct that exploits the idea of a node's \emph{unexplained potential} (the total error channeled through the node) in order to decide where to expand further, mimicking the standard tree construction in a Neural Network setting, alongside a modified gradient descent that first locally optimizes an expanded node before a global optimization. The probabilistic approach allows us to evaluate each new split as a ratio of likelihoods that balance the statistical improvement in explaining the evidence against the additional model complexity --- thus providing a natural stopping condition. The result is a novel classification and regression technique that leverages the strength of both: a tree-structure that grows naturally and is simple to interpret with the plasticity of Neural Networks that allow for soft margins and slanted boundaries.
A Bayesian Decision Tree Algorithm
Jan 11, 2019



Abstract:Bayesian Decision Trees are known for their probabilistic interpretability. However, their construction can sometimes be costly. In this article we present a general Bayesian Decision Tree algorithm applicable to both regression and classification problems. The algorithm does not apply Markov Chain Monte Carlo and does not require a pruning step. While it is possible to construct a weighted probability tree space we find that one particular tree, the greedy-modal tree (GMT), explains most of the information contained in the numerical examples. This approach seems to perform similarly to Random Forests.
An Efficient Algorithm for Bayesian Nearest Neighbours
Jun 02, 2017



Abstract:K-Nearest Neighbours (k-NN) is a popular classification and regression algorithm, yet one of its main limitations is the difficulty in choosing the number of neighbours. We present a Bayesian algorithm to compute the posterior probability distribution for k given a target point within a data-set, efficiently and without the use of Markov Chain Monte Carlo (MCMC) methods or simulation - alongside an exact solution for distributions within the exponential family. The central idea is that data points around our target are generated by the same probability distribution, extending outwards over the appropriate, though unknown, number of neighbours. Once the data is projected onto a distance metric of choice, we can transform the choice of k into a change-point detection problem, for which there is an efficient solution: we recursively compute the probability of the last change-point as we move towards our target, and thus de facto compute the posterior probability distribution over k. Applying this approach to both a classification and a regression UCI data-sets, we compare favourably and, most importantly, by removing the need for simulation, we are able to compute the posterior probability of k exactly and rapidly. As an example, the computational time for the Ripley data-set is a few milliseconds compared to a few hours when using a MCMC approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge