On the Convergence and Stability of Upside-Down Reinforcement Learning, Goal-Conditioned Supervised Learning, and Online Decision Transformers

This article provides a rigorous analysis of convergence and stability of Episodic Upside-Down Reinforcement Learning, Goal-Conditioned Supervised Learning and Online Decision Transformers. These algorithms performed competitively across various benchmarks, from games to robotic tasks, but their theoretical understanding is limited to specific environmental conditions. This work initiates a theoretical foundation for algorithms that build on the broad paradigm of approaching reinforcement learning through supervised learning or sequence modeling. At the core of this investigation lies the analysis of conditions on the underlying environment, under which the algorithms can identify optimal solutions. We also assess whether emerging solutions remain stable in situations where the environment is subject to tiny levels of noise. Specifically, we study the continuity and asymptotic convergence of command-conditioned policies, values and the goal-reaching objective depending on the transition kernel of the underlying Markov Decision Process. We demonstrate that near-optimal behavior is achieved if the transition kernel is located in a sufficiently small neighborhood of a deterministic kernel. The mentioned quantities are continuous (with respect to a specific topology) at deterministic kernels, both asymptotically and after a finite number of learning cycles. The developed methods allow us to present the first explicit estimates on the convergence and stability of policies and values in terms of the underlying transition kernels. On the theoretical side we introduce a number of new concepts to reinforcement learning, like working in segment spaces, studying continuity in quotient topologies and the application of the fixed-point theory of dynamical systems. The theoretical study is accompanied by a detailed investigation of example environments and numerical experiments.

Upside-Down Reinforcement Learning Can Diverge in Stochastic Environments With Episodic Resets

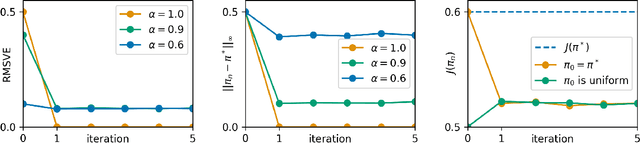
Upside-Down Reinforcement Learning (UDRL) is an approach for solving RL problems that does not require value functions and uses only supervised learning, where the targets for given inputs in a dataset do not change over time. Ghosh et al. proved that Goal-Conditional Supervised Learning (GCSL) -- which can be viewed as a simplified version of UDRL -- optimizes a lower bound on goal-reaching performance. This raises expectations that such algorithms may enjoy guaranteed convergence to the optimal policy in arbitrary environments, similar to certain well-known traditional RL algorithms. Here we show that for a specific episodic UDRL algorithm (eUDRL, including GCSL), this is not the case, and give the causes of this limitation. To do so, we first introduce a helpful rewrite of eUDRL as a recursive policy update. This formulation helps to disprove its convergence to the optimal policy for a wide class of stochastic environments. Finally, we provide a concrete example of a very simple environment where eUDRL diverges. Since the primary aim of this paper is to present a negative result, and the best counterexamples are the simplest ones, we restrict all discussions to finite (discrete) environments, ignoring issues of function approximation and limited sample size.

Reward-Weighted Regression Converges to a Global Optimum

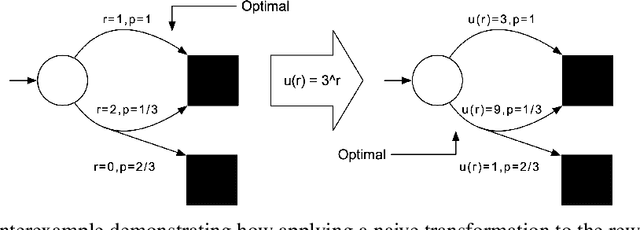
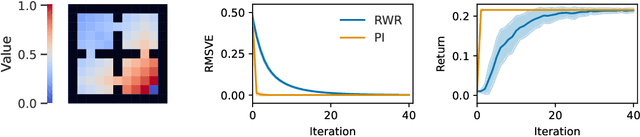
Reward-Weighted Regression (RWR) belongs to a family of widely known iterative Reinforcement Learning algorithms based on the Expectation-Maximization framework. In this family, learning at each iteration consists of sampling a batch of trajectories using the current policy and fitting a new policy to maximize a return-weighted log-likelihood of actions. Although RWR is known to yield monotonic improvement of the policy under certain circumstances, whether and under which conditions RWR converges to the optimal policy have remained open questions. In this paper, we provide for the first time a proof that RWR converges to a global optimum when no function approximation is used.