Upside-Down Reinforcement Learning Can Diverge in Stochastic Environments With Episodic Resets
Paper and Code
May 13, 2022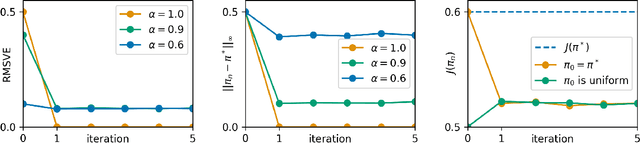
Upside-Down Reinforcement Learning (UDRL) is an approach for solving RL problems that does not require value functions and uses only supervised learning, where the targets for given inputs in a dataset do not change over time. Ghosh et al. proved that Goal-Conditional Supervised Learning (GCSL) -- which can be viewed as a simplified version of UDRL -- optimizes a lower bound on goal-reaching performance. This raises expectations that such algorithms may enjoy guaranteed convergence to the optimal policy in arbitrary environments, similar to certain well-known traditional RL algorithms. Here we show that for a specific episodic UDRL algorithm (eUDRL, including GCSL), this is not the case, and give the causes of this limitation. To do so, we first introduce a helpful rewrite of eUDRL as a recursive policy update. This formulation helps to disprove its convergence to the optimal policy for a wide class of stochastic environments. Finally, we provide a concrete example of a very simple environment where eUDRL diverges. Since the primary aim of this paper is to present a negative result, and the best counterexamples are the simplest ones, we restrict all discussions to finite (discrete) environments, ignoring issues of function approximation and limited sample size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge