Hedging of Financial Derivative Contracts via Monte Carlo Tree Search
Paper and Code
Mar 03, 2021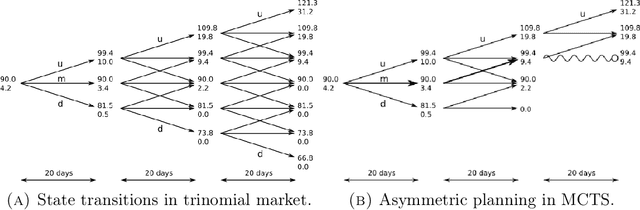
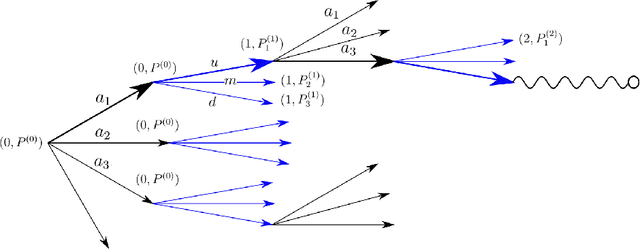
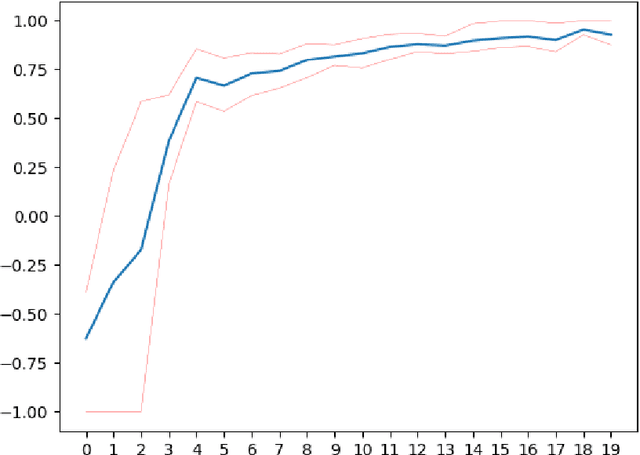
The construction of approximate replication strategies for derivative contracts in incomplete markets is a key problem of financial engineering. Recently Reinforcement Learning algorithms for pricing and hedging under realistic market conditions have attracted significant interest. While financial research mostly focused on variations of $Q$-learning, in Artificial Intelligence Monte Carlo Tree Search is the recognized state-of-the-art method for various planning problems, such as the games of Hex, Chess, Go,... This article introduces Monte Carlo Tree Search as a method to solve the stochastic optimal control problem underlying the pricing and hedging of financial derivatives. As compared to $Q$-learning it combines reinforcement learning with tree search techniques. As a consequence Monte Carlo Tree Search has higher sample efficiency, is less prone to over-fitting to specific market models and generally learns stronger policies faster. In our experiments we find that Monte Carlo Tree Search, being the world-champion in games like Chess and Go, is easily capable of directly maximizing the utility of investor's terminal wealth without an intermediate mathematical theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge