The AI off-switch problem as a signalling game: bounded rationality and incomparability

The off-switch problem is a critical challenge in AI control: if an AI system resists being switched off, it poses a significant risk. In this paper, we model the off-switch problem as a signalling game, where a human decision-maker communicates its preferences about some underlying decision problem to an AI agent, which then selects actions to maximise the human's utility. We assume that the human is a bounded rational agent and explore various bounded rationality mechanisms. Using real machine learning models, we reprove prior results and demonstrate that a necessary condition for an AI system to refrain from disabling its off-switch is its uncertainty about the human's utility. We also analyse how message costs influence optimal strategies and extend the analysis to scenarios involving incomparability.

dynoGP: Deep Gaussian Processes for dynamic system identification

In this work, we present a novel approach to system identification for dynamical systems, based on a specific class of Deep Gaussian Processes (Deep GPs). These models are constructed by interconnecting linear dynamic GPs (equivalent to stochastic linear time-invariant dynamical systems) and static GPs (to model static nonlinearities). Our approach combines the strengths of data-driven methods, such as those based on neural network architectures, with the ability to output a probability distribution. This offers a more comprehensive framework for system identification that includes uncertainty quantification. Using both simulated and real-world data, we demonstrate the effectiveness of the proposed approach.

A Note on Bayesian Networks with Latent Root Variables

We characterise the likelihood function computed from a Bayesian network with latent variables as root nodes. We show that the marginal distribution over the remaining, manifest, variables also factorises as a Bayesian network, which we call empirical. A dataset of observations of the manifest variables allows us to quantify the parameters of the empirical Bayesian net. We prove that (i) the likelihood of such a dataset from the original Bayesian network is dominated by the global maximum of the likelihood from the empirical one; and that (ii) such a maximum is attained if and only if the parameters of the Bayesian network are consistent with those of the empirical model.

Zero-shot Causal Graph Extrapolation from Text via LLMs

We evaluate the ability of large language models (LLMs) to infer causal relations from natural language. Compared to traditional natural language processing and deep learning techniques, LLMs show competitive performance in a benchmark of pairwise relations without needing (explicit) training samples. This motivates us to extend our approach to extrapolating causal graphs through iterated pairwise queries. We perform a preliminary analysis on a benchmark of biomedical abstracts with ground-truth causal graphs validated by experts. The results are promising and support the adoption of LLMs for such a crucial step in causal inference, especially in medical domains, where the amount of scientific text to analyse might be huge, and the causal statements are often implicit.

Tractable Bounding of Counterfactual Queries by Knowledge Compilation

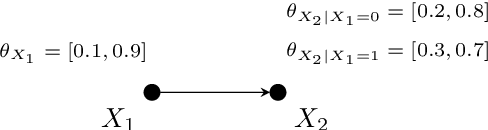
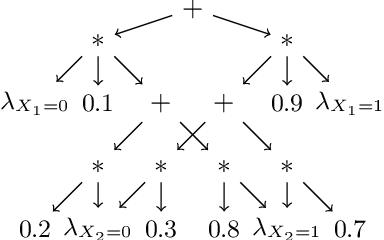
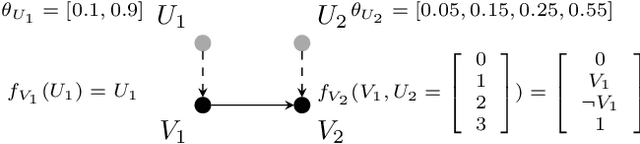
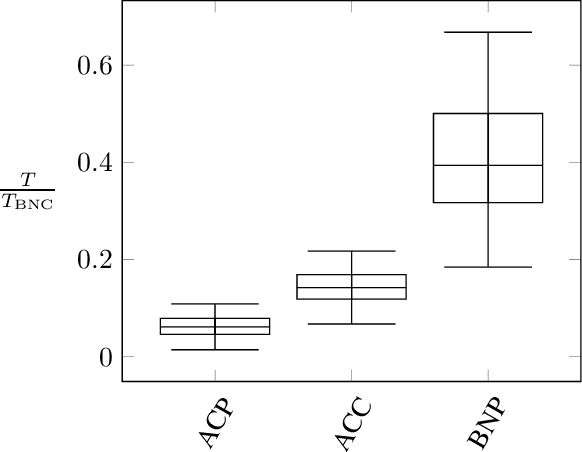
We discuss the problem of bounding partially identifiable queries, such as counterfactuals, in Pearlian structural causal models. A recently proposed iterated EM scheme yields an inner approximation of those bounds by sampling the initialisation parameters. Such a method requires multiple (Bayesian network) queries over models sharing the same structural equations and topology, but different exogenous probabilities. This setup makes a compilation of the underlying model to an arithmetic circuit advantageous, thus inducing a sizeable inferential speed-up. We show how a single symbolic knowledge compilation allows us to obtain the circuit structure with symbolic parameters to be replaced by their actual values when computing the different queries. We also discuss parallelisation techniques to further speed up the bound computation. Experiments against standard Bayesian network inference show clear computational advantages with up to an order of magnitude of speed-up.

Approximating Counterfactual Bounds while Fusing Observational, Biased and Randomised Data Sources

We address the problem of integrating data from multiple, possibly biased, observational and interventional studies, to eventually compute counterfactuals in structural causal models. We start from the case of a single observational dataset affected by a selection bias. We show that the likelihood of the available data has no local maxima. This enables us to use the causal expectation-maximisation scheme to approximate the bounds for partially identifiable counterfactual queries, which are the focus of this paper. We then show how the same approach can address the general case of multiple datasets, no matter whether interventional or observational, biased or unbiased, by remapping it into the former one via graphical transformations. Systematic numerical experiments and a case study on palliative care show the effectiveness of our approach, while hinting at the benefits of fusing heterogeneous data sources to get informative outcomes in case of partial identifiability.

Efficient Computation of Counterfactual Bounds

We assume to be given structural equations over discrete variables inducing a directed acyclic graph, namely, a structural causal model, together with data about its internal nodes. The question we want to answer is how we can compute bounds for partially identifiable counterfactual queries from such an input. We start by giving a map from structural casual models to credal networks. This allows us to compute exact counterfactual bounds via algorithms for credal nets on a subclass of structural causal models. Exact computation is going to be inefficient in general given that, as we show, causal inference is NP-hard even on polytrees. We target then approximate bounds via a causal EM scheme. We evaluate their accuracy by providing credible intervals on the quality of the approximation; we show through a synthetic benchmark that the EM scheme delivers accurate results in a fair number of runs. In the course of the discussion, we also point out what seems to be a neglected limitation to the trending idea that counterfactual bounds can be computed without knowledge of the structural equations. We also present a real case study on palliative care to show how our algorithms can readily be used for practical purposes.

Learning to Bound Counterfactual Inference in Structural Causal Models from Observational and Randomised Data

We address the problem of integrating data from multiple observational and interventional studies to eventually compute counterfactuals in structural causal models. We derive a likelihood characterisation for the overall data that leads us to extend a previous EM-based algorithm from the case of a single study to that of multiple ones. The new algorithm learns to approximate the (unidentifiability) region of model parameters from such mixed data sources. On this basis, it delivers interval approximations to counterfactual results, which collapse to points in the identifiable case. The algorithm is very general, it works on semi-Markovian models with discrete variables and can compute any counterfactual. Moreover, it automatically determines if a problem is feasible (the parameter region being nonempty), which is a necessary step not to yield incorrect results. Systematic numerical experiments show the effectiveness and accuracy of the algorithm, while hinting at the benefits of integrating heterogeneous data to get informative bounds in case of unidentifiability.

Nonlinear desirability theory

Desirability can be understood as an extension of Anscombe and Aumann's Bayesian decision theory to sets of expected utilities. At the core of desirability lies an assumption of linearity of the scale in which rewards are measured. It is a traditional assumption used to derive the expected utility model, which clashes with a general representation of rational decision making, though. Allais has, in particular, pointed this out in 1953 with his famous paradox. We note that the utility scale plays the role of a closure operator when we regard desirability as a logical theory. This observation enables us to extend desirability to the nonlinear case by letting the utility scale be represented via a general closure operator. The new theory directly expresses rewards in actual nonlinear currency (money), much in Savage's spirit, while arguably weakening the founding assumptions to a minimum. We characterise the main properties of the new theory both from the perspective of sets of gambles and of their lower and upper prices (previsions). We show how Allais paradox finds a solution in the new theory, and discuss the role of sets of probabilities in the theory.

Bounding Counterfactuals under Selection Bias

Causal analysis may be affected by selection bias, which is defined as the systematic exclusion of data from a certain subpopulation. Previous work in this area focused on the derivation of identifiability conditions. We propose instead a first algorithm to address both identifiable and unidentifiable queries. We prove that, in spite of the missingness induced by the selection bias, the likelihood of the available data is unimodal. This enables us to use the causal expectation-maximisation scheme to obtain the values of causal queries in the identifiable case, and to compute bounds otherwise. Experiments demonstrate the approach to be practically viable. Theoretical convergence characterisations are provided.