Constrained Identifiability of Causal Effects

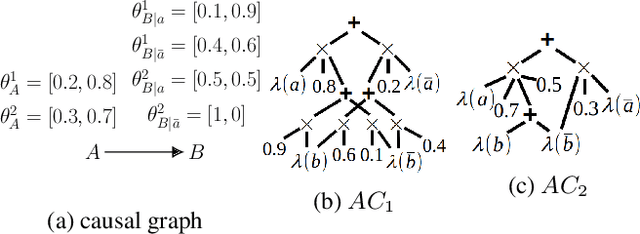
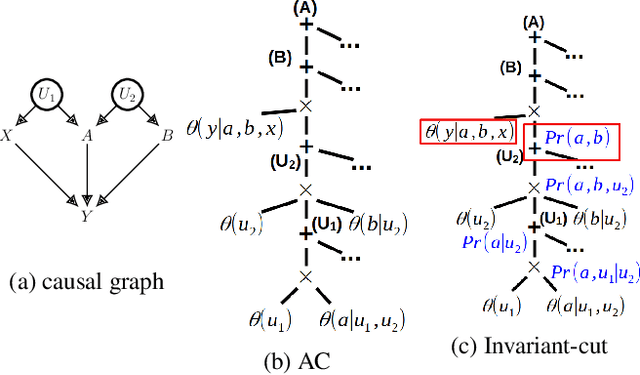
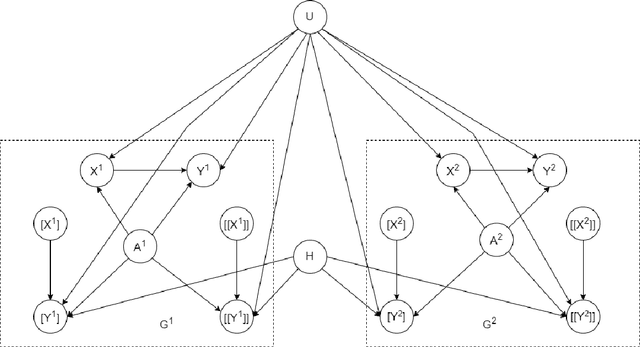
We study the identification of causal effects in the presence of different types of constraints (e.g., logical constraints) in addition to the causal graph. These constraints impose restrictions on the models (parameterizations) induced by the causal graph, reducing the set of models considered by the identifiability problem. We formalize the notion of constrained identifiability, which takes a set of constraints as another input to the classical definition of identifiability. We then introduce a framework for testing constrained identifiability by employing tractable Arithmetic Circuits (ACs), which enables us to accommodate constraints systematically. We show that this AC-based approach is at least as complete as existing algorithms (e.g., do-calculus) for testing classical identifiability, which only assumes the constraint of strict positivity. We use examples to demonstrate the effectiveness of this AC-based approach by showing that unidentifiable causal effects may become identifiable under different types of constraints.

Causal Unit Selection using Tractable Arithmetic Circuits

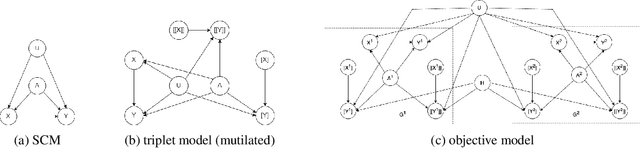
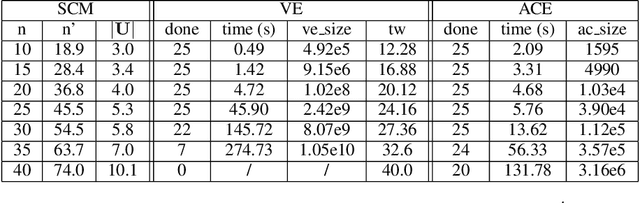
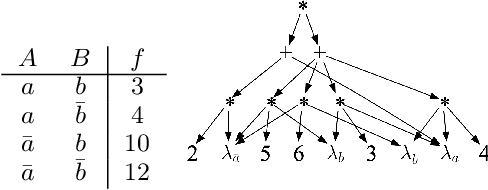
The unit selection problem aims to find objects, called units, that optimize a causal objective function which describes the objects' behavior in a causal context (e.g., selecting customers who are about to churn but would most likely change their mind if encouraged). While early studies focused mainly on bounding a specific class of counterfactual objective functions using data, more recent work allows one to find optimal units exactly by reducing the causal objective to a classical objective on a meta-model, and then applying a variant of the classical Variable Elimination (VE) algorithm to the meta-model -- assuming a fully specified causal model is available. In practice, however, finding optimal units using this approach can be very expensive because the used VE algorithm must be exponential in the constrained treewidth of the meta-model, which is larger and denser than the original model. We address this computational challenge by introducing a new approach for unit selection that is not necessarily limited by the constrained treewidth. This is done through compiling the meta-model into a special class of tractable arithmetic circuits that allows the computation of optimal units in time linear in the circuit size. We finally present empirical results on random causal models that show order-of-magnitude speedups based on the proposed method for solving unit selection.

Identifying Causal Effects Under Functional Dependencies

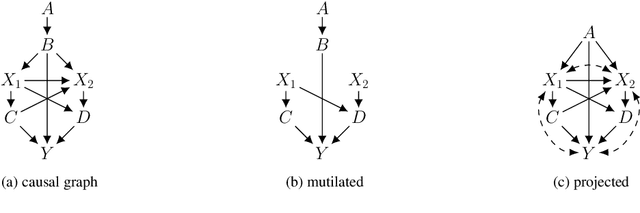
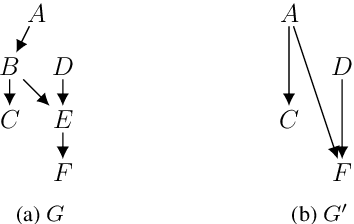
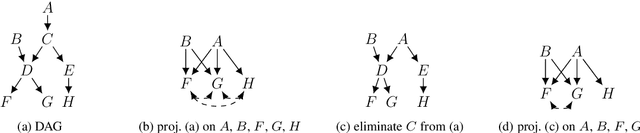
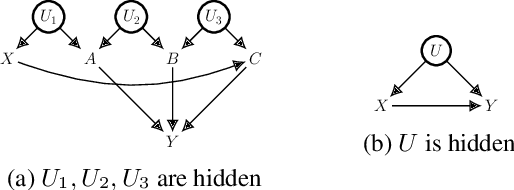
We study the identification of causal effects, motivated by two improvements to identifiability which can be attained if one knows that some variables in a causal graph are functionally determined by their parents (without needing to know the specific functions). First, an unidentifiable causal effect may become identifiable when certain variables are functional. Second, certain functional variables can be excluded from being observed without affecting the identifiability of a causal effect, which may significantly reduce the number of needed variables in observational data. Our results are largely based on an elimination procedure which removes functional variables from a causal graph while preserving key properties in the resulting causal graph, including the identifiability of causal effects.

Tractable Bounding of Counterfactual Queries by Knowledge Compilation

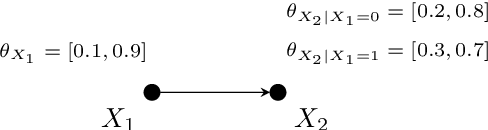
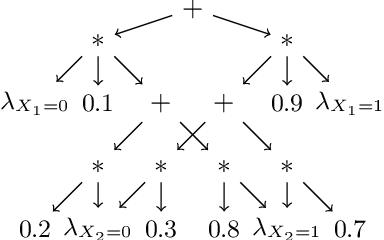
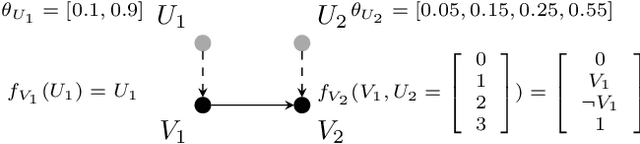
We discuss the problem of bounding partially identifiable queries, such as counterfactuals, in Pearlian structural causal models. A recently proposed iterated EM scheme yields an inner approximation of those bounds by sampling the initialisation parameters. Such a method requires multiple (Bayesian network) queries over models sharing the same structural equations and topology, but different exogenous probabilities. This setup makes a compilation of the underlying model to an arithmetic circuit advantageous, thus inducing a sizeable inferential speed-up. We show how a single symbolic knowledge compilation allows us to obtain the circuit structure with symbolic parameters to be replaced by their actual values when computing the different queries. We also discuss parallelisation techniques to further speed up the bound computation. Experiments against standard Bayesian network inference show clear computational advantages with up to an order of magnitude of speed-up.

Logic for Explainable AI

A central quest in explainable AI relates to understanding the decisions made by (learned) classifiers. There are three dimensions of this understanding that have been receiving significant attention in recent years. The first dimension relates to characterizing conditions on instances that are necessary and sufficient for decisions, therefore providing abstractions of instances that can be viewed as the "reasons behind decisions." The next dimension relates to characterizing minimal conditions that are sufficient for a decision, therefore identifying maximal aspects of the instance that are irrelevant to the decision. The last dimension relates to characterizing minimal conditions that are necessary for a decision, therefore identifying minimal perturbations to the instance that yield alternate decisions. We discuss in this tutorial a comprehensive, semantical and computational theory of explainability along these dimensions which is based on some recent developments in symbolic logic. The tutorial will also discuss how this theory is particularly applicable to non-symbolic classifiers such as those based on Bayesian networks, decision trees, random forests and some types of neural networks.

A New Class of Explanations for Classifiers with Non-Binary Features

Two types of explanations have received significant attention in the literature recently when analyzing the decisions made by classifiers. The first type explains why a decision was made and is known as a sufficient reason for the decision, also an abductive or PI-explanation. The second type explains why some other decision was not made and is known as a necessary reason for the decision, also a contrastive or counterfactual explanation. These explanations were defined for classifiers with binary, discrete and, in some cases, continuous features. We show that these explanations can be significantly improved in the presence of non-binary features, leading to a new class of explanations that relay more information about decisions and the underlying classifiers. Necessary and sufficient reasons were also shown to be the prime implicates and implicants of the complete reason for a decision, which can be obtained using a quantification operator. We show that our improved notions of necessary and sufficient reasons are also prime implicates and implicants but for an improved notion of complete reason obtained by a new quantification operator that we define and study in this paper.

An Algorithm and Complexity Results for Causal Unit Selection

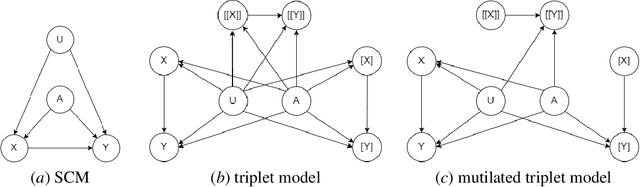
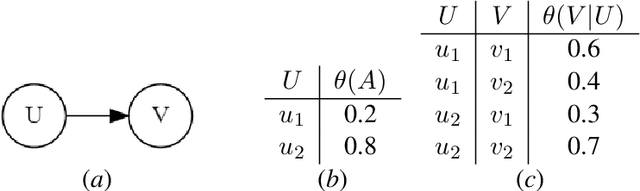
The unit selection problem aims to identify objects, called units, that are most likely to exhibit a desired mode of behavior when subjected to stimuli (e.g., customers who are about to churn but would change their mind if encouraged). Unit selection with counterfactual objective functions was introduced relatively recently with existing work focusing on bounding a specific class of objective functions, called the benefit functions, based on observational and interventional data -- assuming a fully specified model is not available to evaluate these functions. We complement this line of work by proposing the first exact algorithm for finding optimal units given a broad class of causal objective functions and a fully specified structural causal model (SCM). We show that unit selection under this class of objective functions is $\text{NP}^\text{PP}$-complete but is $\text{NP}$-complete when unit variables correspond to all exogenous variables in the SCM. We also provide treewidth-based complexity bounds on our proposed algorithm while relating it to a well-known algorithm for Maximum a Posteriori (MAP) inference.

On the Complexity of Counterfactual Reasoning

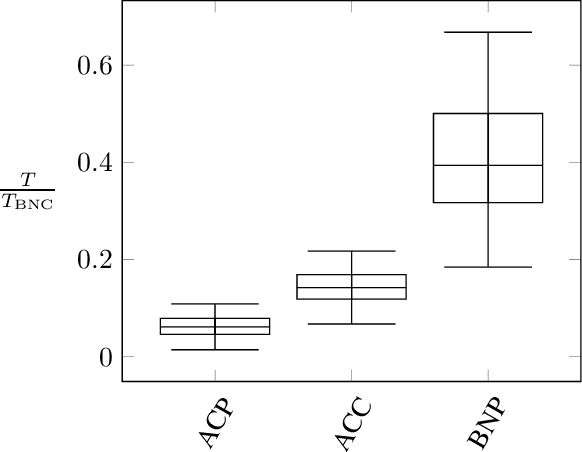
We study the computational complexity of counterfactual reasoning in relation to the complexity of associational and interventional reasoning on structural causal models (SCMs). We show that counterfactual reasoning is no harder than associational or interventional reasoning on fully specified SCMs in the context of two computational frameworks. The first framework is based on the notion of treewidth and includes the classical variable elimination and jointree algorithms. The second framework is based on the more recent and refined notion of causal treewidth which is directed towards models with functional dependencies such as SCMs. Our results are constructive and based on bounding the (causal) treewidth of twin networks -- used in standard counterfactual reasoning that contemplates two worlds, real and imaginary -- to the (causal) treewidth of the underlying SCM structure. In particular, we show that the latter (causal) treewidth is no more than twice the former plus one. Hence, if associational or interventional reasoning is tractable on a fully specified SCM then counterfactual reasoning is tractable too. We extend our results to general counterfactual reasoning that requires contemplating more than two worlds and discuss applications of our results to counterfactual reasoning with a partially specified SCM that is coupled with data. We finally present empirical results that measure the gap between the complexities of counterfactual reasoning and associational/interventional reasoning on random SCMs.

On the Computation of Necessary and Sufficient Explanations

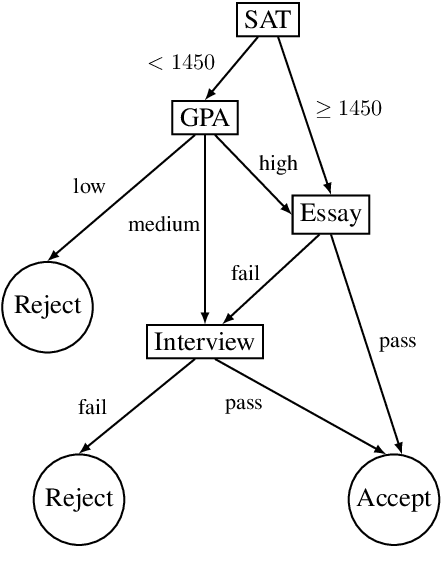
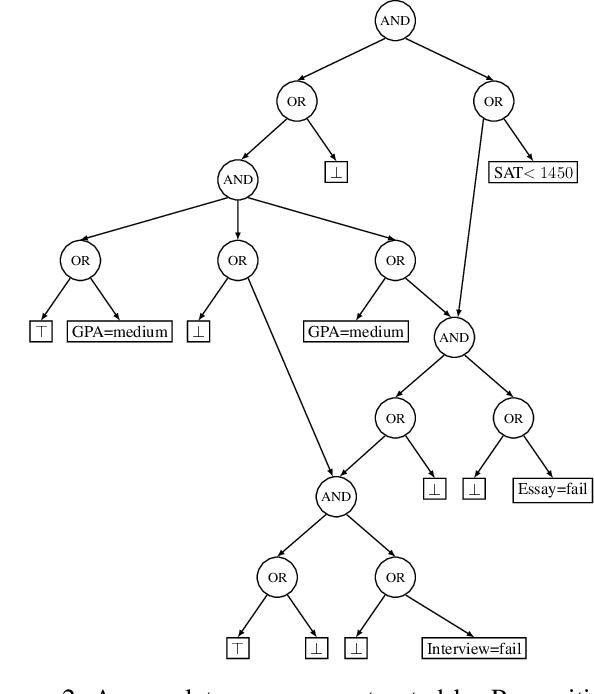
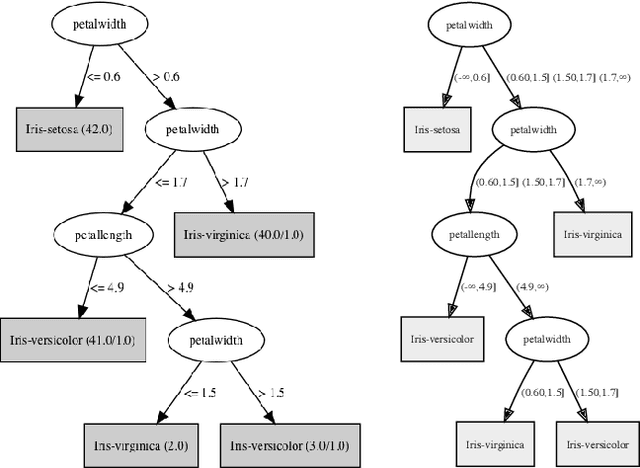
The complete reason behind a decision is a Boolean formula that characterizes why the decision was made. This recently introduced notion has a number of applications, which include generating explanations, detecting decision bias and evaluating counterfactual queries. Prime implicants of the complete reason are known as sufficient reasons for the decision and they correspond to what is known as PI explanations and abductive explanations. In this paper, we refer to the prime implicates of a complete reason as necessary reasons for the decision. We justify this terminology semantically and show that necessary reasons correspond to what is known as contrastive explanations. We also study the computation of complete reasons for multi-class decision trees and graphs with nominal and numeric features for which we derive efficient, closed-form complete reasons. We further investigate the computation of shortest necessary and sufficient reasons for a broad class of complete reasons, which include the derived closed forms and the complete reasons for Sentential Decision Diagrams (SDDs). We provide an algorithm which can enumerate their shortest necessary reasons in output polynomial time. Enumerating shortest sufficient reasons for this class of complete reasons is hard even for a single reason. For this problem, we provide an algorithm that appears to be quite efficient as we show empirically.

Tractable Boolean and Arithmetic Circuits

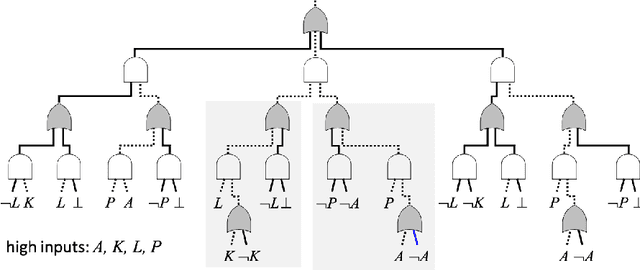
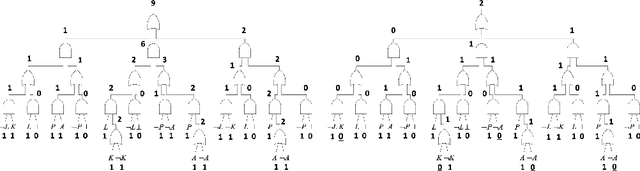
Tractable Boolean and arithmetic circuits have been studied extensively in AI for over two decades now. These circuits were initially proposed as "compiled objects," meant to facilitate logical and probabilistic reasoning, as they permit various types of inference to be performed in linear-time and a feed-forward fashion like neural networks. In more recent years, the role of tractable circuits has significantly expanded as they became a computational and semantical backbone for some approaches that aim to integrate knowledge, reasoning and learning. In this article, we review the foundations of tractable circuits and some associated milestones, while focusing on their core properties and techniques that make them particularly useful for the broad aims of neuro-symbolic AI.