An Algorithm and Complexity Results for Causal Unit Selection
Paper and Code
Feb 28, 2023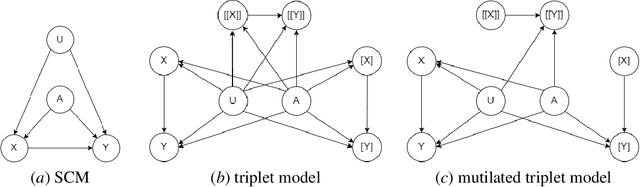
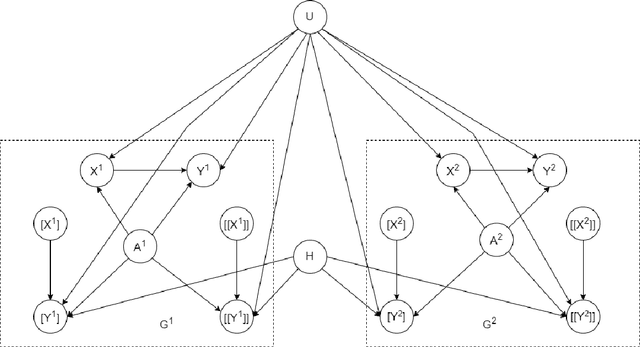
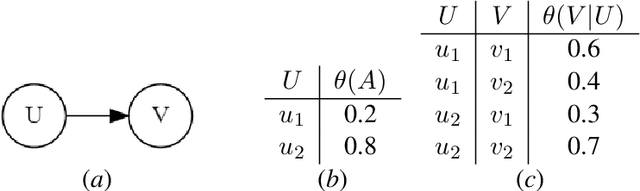
The unit selection problem aims to identify objects, called units, that are most likely to exhibit a desired mode of behavior when subjected to stimuli (e.g., customers who are about to churn but would change their mind if encouraged). Unit selection with counterfactual objective functions was introduced relatively recently with existing work focusing on bounding a specific class of objective functions, called the benefit functions, based on observational and interventional data -- assuming a fully specified model is not available to evaluate these functions. We complement this line of work by proposing the first exact algorithm for finding optimal units given a broad class of causal objective functions and a fully specified structural causal model (SCM). We show that unit selection under this class of objective functions is $\text{NP}^\text{PP}$-complete but is $\text{NP}$-complete when unit variables correspond to all exogenous variables in the SCM. We also provide treewidth-based complexity bounds on our proposed algorithm while relating it to a well-known algorithm for Maximum a Posteriori (MAP) inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge