PR-CapsNet: Pseudo-Riemannian Capsule Network with Adaptive Curvature Routing for Graph Learning

Capsule Networks (CapsNets) show exceptional graph representation capacity via dynamic routing and vectorized hierarchical representations, but they model the complex geometries of real\-world graphs poorly by fixed\-curvature space due to the inherent geodesical disconnectedness issues, leading to suboptimal performance. Recent works find that non\-Euclidean pseudo\-Riemannian manifolds provide specific inductive biases for embedding graph data, but how to leverage them to improve CapsNets is still underexplored. Here, we extend the Euclidean capsule routing into geodesically disconnected pseudo\-Riemannian manifolds and derive a Pseudo\-Riemannian Capsule Network (PR\-CapsNet), which models data in pseudo\-Riemannian manifolds of adaptive curvature, for graph representation learning. Specifically, PR\-CapsNet enhances the CapsNet with Adaptive Pseudo\-Riemannian Tangent Space Routing by utilizing pseudo\-Riemannian geometry. Unlike single\-curvature or subspace\-partitioning methods, PR\-CapsNet concurrently models hierarchical and cluster or cyclic graph structures via its versatile pseudo\-Riemannian metric. It first deploys Pseudo\-Riemannian Tangent Space Routing to decompose capsule states into spherical\-temporal and Euclidean\-spatial subspaces with diffeomorphic transformations. Then, an Adaptive Curvature Routing is developed to adaptively fuse features from different curvature spaces for complex graphs via a learnable curvature tensor with geometric attention from local manifold properties. Finally, a geometric properties\-preserved Pseudo\-Riemannian Capsule Classifier is developed to project capsule embeddings to tangent spaces and use curvature\-weighted softmax for classification. Extensive experiments on node and graph classification benchmarks show PR\-CapsNet outperforms SOTA models, validating PR\-CapsNet's strong representation power for complex graph structures.

Causal Unit Selection using Tractable Arithmetic Circuits

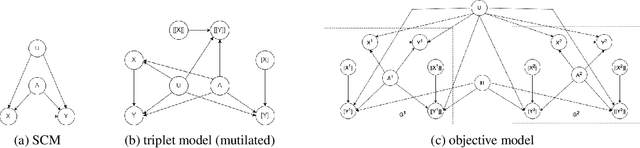
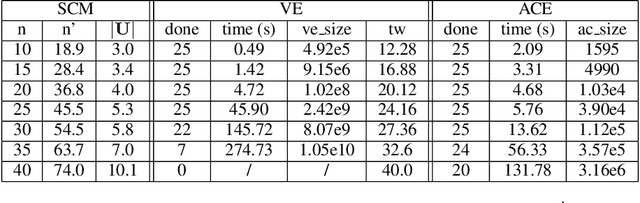
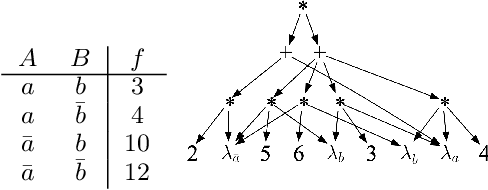
The unit selection problem aims to find objects, called units, that optimize a causal objective function which describes the objects' behavior in a causal context (e.g., selecting customers who are about to churn but would most likely change their mind if encouraged). While early studies focused mainly on bounding a specific class of counterfactual objective functions using data, more recent work allows one to find optimal units exactly by reducing the causal objective to a classical objective on a meta-model, and then applying a variant of the classical Variable Elimination (VE) algorithm to the meta-model -- assuming a fully specified causal model is available. In practice, however, finding optimal units using this approach can be very expensive because the used VE algorithm must be exponential in the constrained treewidth of the meta-model, which is larger and denser than the original model. We address this computational challenge by introducing a new approach for unit selection that is not necessarily limited by the constrained treewidth. This is done through compiling the meta-model into a special class of tractable arithmetic circuits that allows the computation of optimal units in time linear in the circuit size. We finally present empirical results on random causal models that show order-of-magnitude speedups based on the proposed method for solving unit selection.

An Algorithm and Complexity Results for Causal Unit Selection

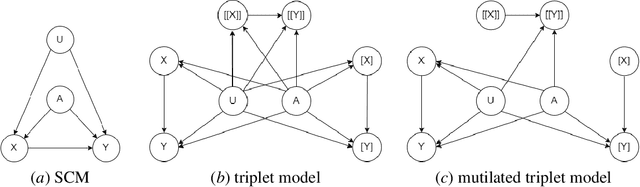
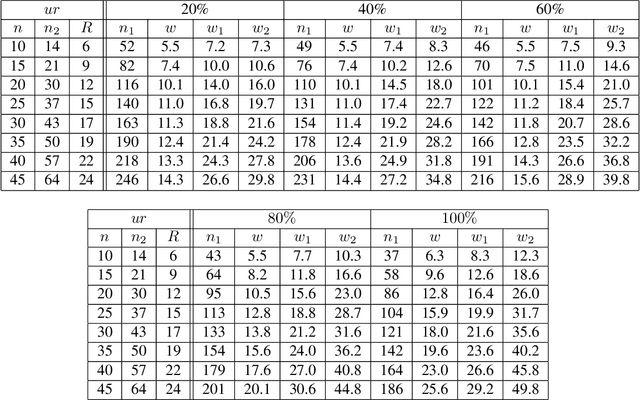
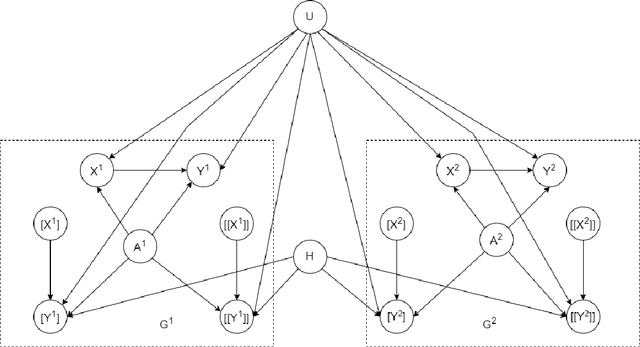
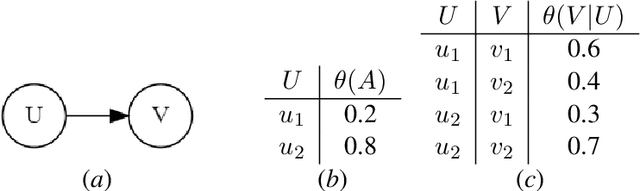
The unit selection problem aims to identify objects, called units, that are most likely to exhibit a desired mode of behavior when subjected to stimuli (e.g., customers who are about to churn but would change their mind if encouraged). Unit selection with counterfactual objective functions was introduced relatively recently with existing work focusing on bounding a specific class of objective functions, called the benefit functions, based on observational and interventional data -- assuming a fully specified model is not available to evaluate these functions. We complement this line of work by proposing the first exact algorithm for finding optimal units given a broad class of causal objective functions and a fully specified structural causal model (SCM). We show that unit selection under this class of objective functions is $\text{NP}^\text{PP}$-complete but is $\text{NP}$-complete when unit variables correspond to all exogenous variables in the SCM. We also provide treewidth-based complexity bounds on our proposed algorithm while relating it to a well-known algorithm for Maximum a Posteriori (MAP) inference.