Causal Unit Selection using Tractable Arithmetic Circuits

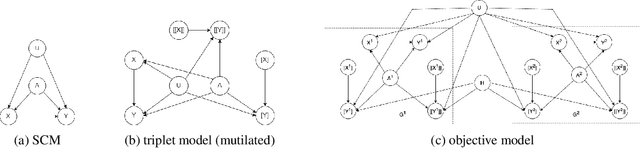
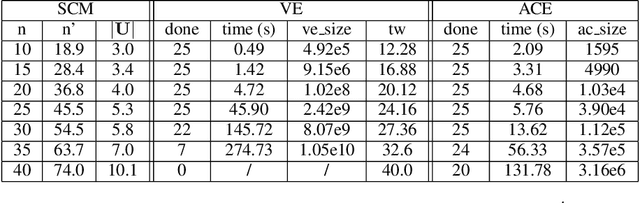
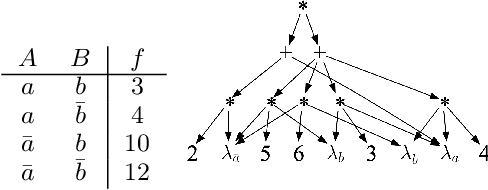
The unit selection problem aims to find objects, called units, that optimize a causal objective function which describes the objects' behavior in a causal context (e.g., selecting customers who are about to churn but would most likely change their mind if encouraged). While early studies focused mainly on bounding a specific class of counterfactual objective functions using data, more recent work allows one to find optimal units exactly by reducing the causal objective to a classical objective on a meta-model, and then applying a variant of the classical Variable Elimination (VE) algorithm to the meta-model -- assuming a fully specified causal model is available. In practice, however, finding optimal units using this approach can be very expensive because the used VE algorithm must be exponential in the constrained treewidth of the meta-model, which is larger and denser than the original model. We address this computational challenge by introducing a new approach for unit selection that is not necessarily limited by the constrained treewidth. This is done through compiling the meta-model into a special class of tractable arithmetic circuits that allows the computation of optimal units in time linear in the circuit size. We finally present empirical results on random causal models that show order-of-magnitude speedups based on the proposed method for solving unit selection.