Constrained Identifiability of Causal Effects
Paper and Code
Dec 03, 2024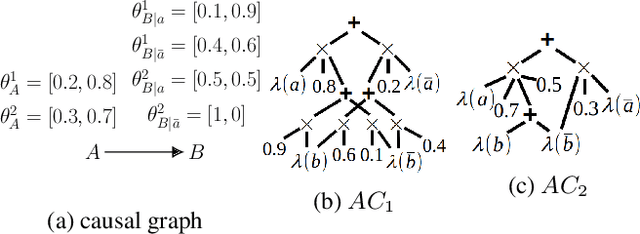
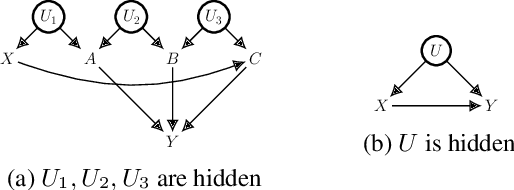
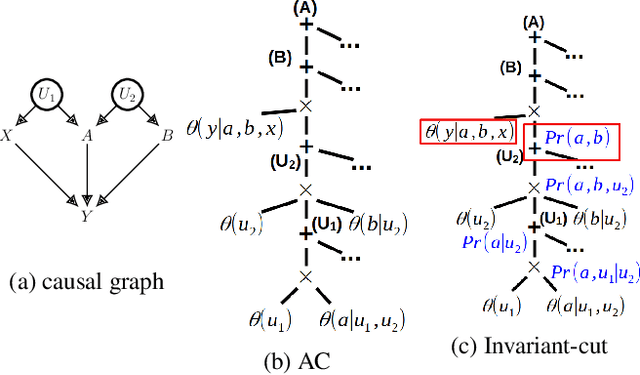
We study the identification of causal effects in the presence of different types of constraints (e.g., logical constraints) in addition to the causal graph. These constraints impose restrictions on the models (parameterizations) induced by the causal graph, reducing the set of models considered by the identifiability problem. We formalize the notion of constrained identifiability, which takes a set of constraints as another input to the classical definition of identifiability. We then introduce a framework for testing constrained identifiability by employing tractable Arithmetic Circuits (ACs), which enables us to accommodate constraints systematically. We show that this AC-based approach is at least as complete as existing algorithms (e.g., do-calculus) for testing classical identifiability, which only assumes the constraint of strict positivity. We use examples to demonstrate the effectiveness of this AC-based approach by showing that unidentifiable causal effects may become identifiable under different types of constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge