How do Machine Learning Models Change?

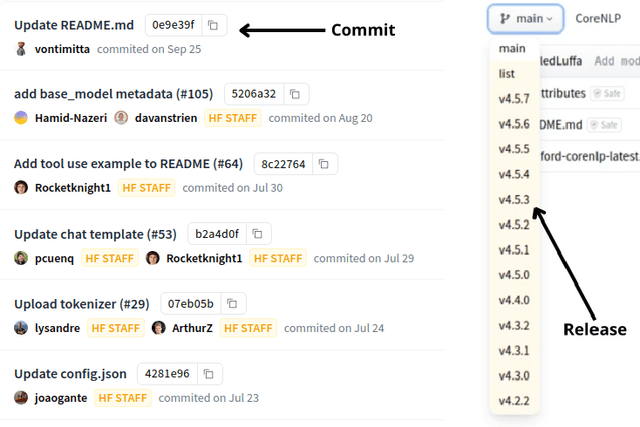
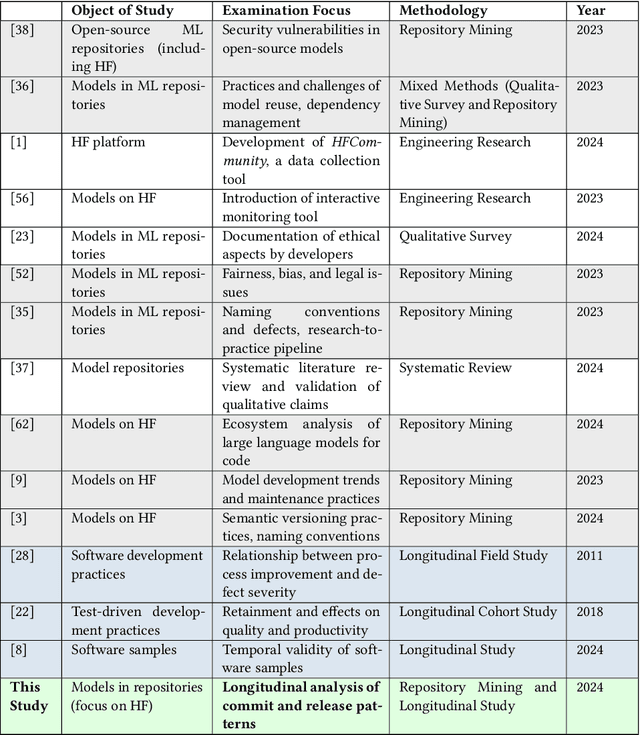
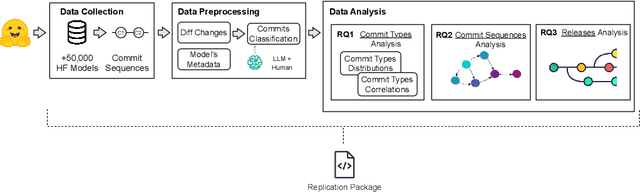
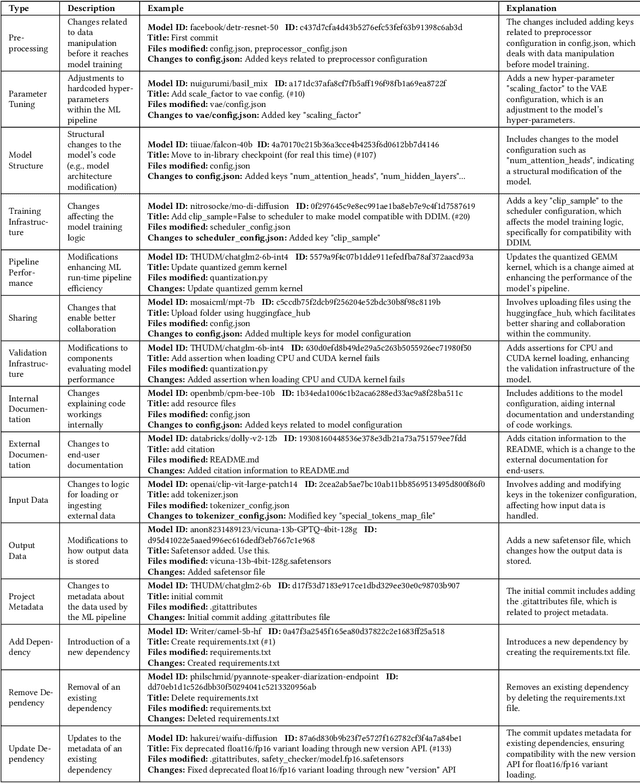
The proliferation of Machine Learning (ML) models and their open-source implementations has transformed Artificial Intelligence research and applications. Platforms like Hugging Face (HF) enable the development, sharing, and deployment of these models, fostering an evolving ecosystem. While previous studies have examined aspects of models hosted on platforms like HF, a comprehensive longitudinal study of how these models change remains underexplored. This study addresses this gap by utilizing both repository mining and longitudinal analysis methods to examine over 200,000 commits and 1,200 releases from over 50,000 models on HF. We replicate and extend an ML change taxonomy for classifying commits and utilize Bayesian networks to uncover patterns in commit and release activities over time. Our findings indicate that commit activities align with established data science methodologies, such as CRISP-DM, emphasizing iterative refinement and continuous improvement. Additionally, release patterns tend to consolidate significant updates, particularly in documentation, distinguishing between granular changes and milestone-based releases. Furthermore, projects with higher popularity prioritize infrastructure enhancements early in their lifecycle, and those with intensive collaboration practices exhibit improved documentation standards. These and other insights enhance the understanding of model changes on community platforms and provide valuable guidance for best practices in model maintenance.

Counterfactual Reasoning with Probabilistic Graphical Models for Analyzing Socioecological Systems

Causal and counterfactual reasoning are emerging directions in data science that allow us to reason about hypothetical scenarios. This is particularly useful in domains where experimental data are usually not available. In the context of environmental and ecological sciences, causality enables us, for example, to predict how an ecosystem would respond to hypothetical interventions. A structural causal model is a class of probabilistic graphical models for causality, which, due to its intuitive nature, can be easily understood by experts in multiple fields. However, certain queries, called unidentifiable, cannot be calculated in an exact and precise manner. This paper proposes applying a novel and recent technique for bounding unidentifiable queries within the domain of socioecological systems. Our findings indicate that traditional statistical analysis, including probabilistic graphical models, can identify the influence between variables. However, such methods do not offer insights into the nature of the relationship, specifically whether it involves necessity or sufficiency. This is where counterfactual reasoning becomes valuable.

Approximating Counterfactual Bounds while Fusing Observational, Biased and Randomised Data Sources

We address the problem of integrating data from multiple, possibly biased, observational and interventional studies, to eventually compute counterfactuals in structural causal models. We start from the case of a single observational dataset affected by a selection bias. We show that the likelihood of the available data has no local maxima. This enables us to use the causal expectation-maximisation scheme to approximate the bounds for partially identifiable counterfactual queries, which are the focus of this paper. We then show how the same approach can address the general case of multiple datasets, no matter whether interventional or observational, biased or unbiased, by remapping it into the former one via graphical transformations. Systematic numerical experiments and a case study on palliative care show the effectiveness of our approach, while hinting at the benefits of fusing heterogeneous data sources to get informative outcomes in case of partial identifiability.

Efficient Computation of Counterfactual Bounds

We assume to be given structural equations over discrete variables inducing a directed acyclic graph, namely, a structural causal model, together with data about its internal nodes. The question we want to answer is how we can compute bounds for partially identifiable counterfactual queries from such an input. We start by giving a map from structural casual models to credal networks. This allows us to compute exact counterfactual bounds via algorithms for credal nets on a subclass of structural causal models. Exact computation is going to be inefficient in general given that, as we show, causal inference is NP-hard even on polytrees. We target then approximate bounds via a causal EM scheme. We evaluate their accuracy by providing credible intervals on the quality of the approximation; we show through a synthetic benchmark that the EM scheme delivers accurate results in a fair number of runs. In the course of the discussion, we also point out what seems to be a neglected limitation to the trending idea that counterfactual bounds can be computed without knowledge of the structural equations. We also present a real case study on palliative care to show how our algorithms can readily be used for practical purposes.

Learning to Bound Counterfactual Inference in Structural Causal Models from Observational and Randomised Data

We address the problem of integrating data from multiple observational and interventional studies to eventually compute counterfactuals in structural causal models. We derive a likelihood characterisation for the overall data that leads us to extend a previous EM-based algorithm from the case of a single study to that of multiple ones. The new algorithm learns to approximate the (unidentifiability) region of model parameters from such mixed data sources. On this basis, it delivers interval approximations to counterfactual results, which collapse to points in the identifiable case. The algorithm is very general, it works on semi-Markovian models with discrete variables and can compute any counterfactual. Moreover, it automatically determines if a problem is feasible (the parameter region being nonempty), which is a necessary step not to yield incorrect results. Systematic numerical experiments show the effectiveness and accuracy of the algorithm, while hinting at the benefits of integrating heterogeneous data to get informative bounds in case of unidentifiability.

Bounding Counterfactuals under Selection Bias

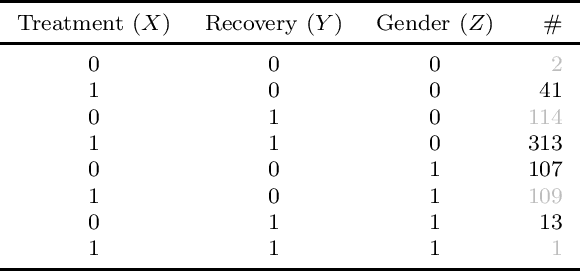
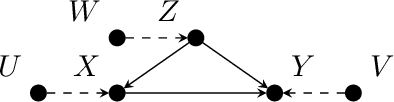
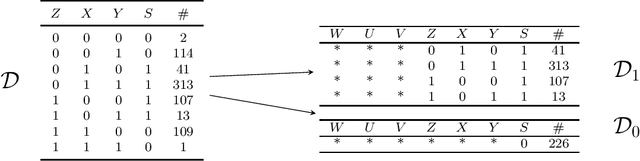
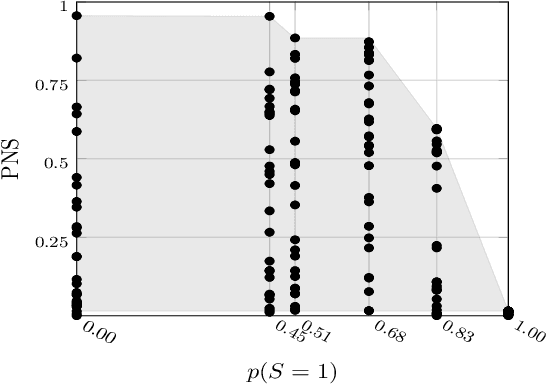
Causal analysis may be affected by selection bias, which is defined as the systematic exclusion of data from a certain subpopulation. Previous work in this area focused on the derivation of identifiability conditions. We propose instead a first algorithm to address both identifiable and unidentifiable queries. We prove that, in spite of the missingness induced by the selection bias, the likelihood of the available data is unimodal. This enables us to use the causal expectation-maximisation scheme to obtain the values of causal queries in the identifiable case, and to compute bounds otherwise. Experiments demonstrate the approach to be practically viable. Theoretical convergence characterisations are provided.

Diversity and Generalization in Neural Network Ensembles

Ensembles are widely used in machine learning and, usually, provide state-of-the-art performance in many prediction tasks. From the very beginning, the diversity of an ensemble has been identified as a key factor for the superior performance of these models. But the exact role that diversity plays in ensemble models is poorly understood, specially in the context of neural networks. In this work, we combine and expand previously published results in a theoretically sound framework that describes the relationship between diversity and ensemble performance for a wide range of ensemble methods. More precisely, we provide sound answers to the following questions: how to measure diversity, how diversity relates to the generalization error of an ensemble, and how diversity is promoted by neural network ensemble algorithms. This analysis covers three widely used loss functions, namely, the squared loss, the cross-entropy loss, and the 0-1 loss; and two widely used model combination strategies, namely, model averaging and weighted majority vote. We empirically validate this theoretical analysis with neural network ensembles.

CREPO: An Open Repository to Benchmark Credal Network Algorithms

Credal networks are a popular class of imprecise probabilistic graphical models obtained as a Bayesian network generalization based on, so-called credal, sets of probability mass functions. A Java library called CREMA has been recently released to model, process and query credal networks. Despite the NP-hardness of the (exact) task, a number of algorithms is available to approximate credal network inferences. In this paper we present CREPO, an open repository of synthetic credal networks, provided together with the exact results of inference tasks on these models. A Python tool is also delivered to load these data and interact with CREMA, thus making extremely easy to evaluate and compare existing and novel inference algorithms. To demonstrate such benchmarking scheme, we propose an approximate heuristic to be used inside variable elimination schemes to keep a bound on the maximum number of vertices generated during the combination step. A CREPO-based validation against approximate procedures based on linearization and exact techniques performed in CREMA is finally discussed.

EM Based Bounding of Unidentifiable Queries in Structural Causal Models

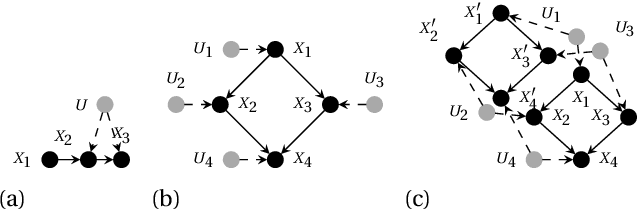
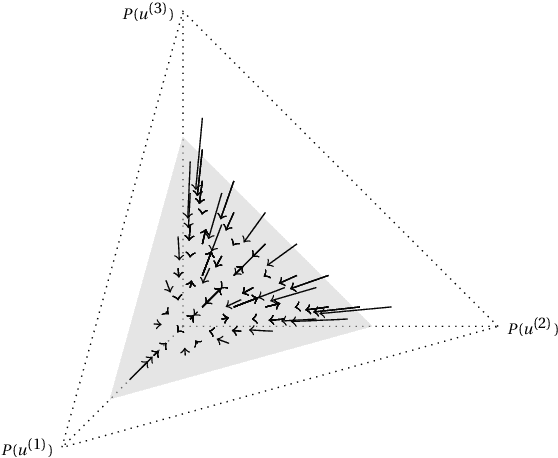
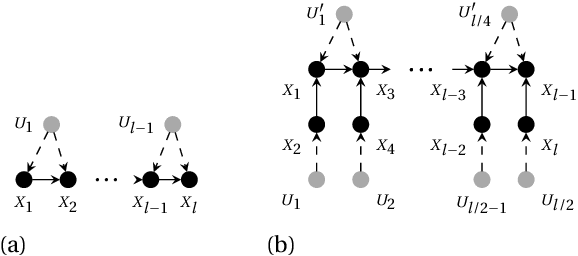
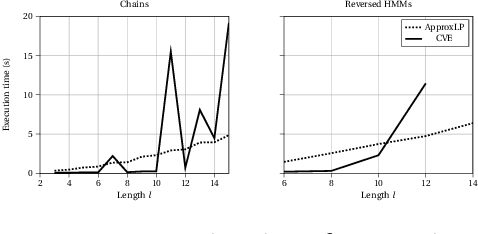
A structural causal model is made of endogenous (manifest) and exogenous (latent) variables. In a recent paper, it has been shown that endogenous observations induce linear constraints on the probabilities of the exogenous variables. This allows to exactly map a causal model into a \emph{credal network}. Causal inferences, such as interventions and counterfactuals, can consequently be obtained by standard credal network algorithms. These natively return sharp values in the identifiable case, while intervals corresponding to the exact bounds are produced for unidentifiable queries. In this paper we present an approximate characterization of the constraints on the exogenous probabilities. This is based on a specialization of the EM algorithm to the treatment of the missing values in the exogenous observations. Multiple EM runs can be consequently used to describe the causal model as a set of Bayesian networks and, hence, a credal network to be queried for the bounding of unidentifiable queries. Preliminary empirical tests show how this approach might provide good inner bounds with relatively few runs. This is a promising direction for causal analysis in models whose topology prevents a straightforward specification of the credal mapping.

Structural Causal Models Are (Solvable by) Credal Networks

A structural causal model is made of endogenous (manifest) and exogenous (latent) variables. We show that endogenous observations induce linear constraints on the probabilities of the exogenous variables. This allows to exactly map a causal model into a credal network. Causal inferences, such as interventions and counterfactuals, can consequently be obtained by standard algorithms for the updating of credal nets. These natively return sharp values in the identifiable case, while intervals corresponding to the exact bounds are produced for unidentifiable queries. A characterization of the causal models that allow the map above to be compactly derived is given, along with a discussion about the scalability for general models. This contribution should be regarded as a systematic approach to represent structural causal models by credal networks and hence to systematically compute causal inferences. A number of demonstrative examples is presented to clarify our methodology. Extensive experiments show that approximate algorithms for credal networks can immediately be used to do causal inference in real-size problems.