PAC-Bayes-Chernoff bounds for unbounded losses

We present a new high-probability PAC-Bayes oracle bound for unbounded losses. This result can be understood as a PAC-Bayes version of the Chernoff bound. The proof technique relies on uniformly bounding the tail of certain random variable based on the Cram\'er transform of the loss. We highlight two applications of our main result. First, we show that our bound solves the open problem of optimizing the free parameter on many PAC-Bayes bounds. Finally, we show that our approach allows working with flexible assumptions on the loss function, resulting in novel bounds that generalize previous ones and can be minimized to obtain Gibbs-like posteriors.

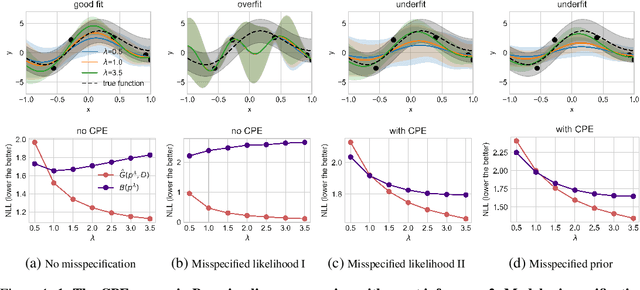
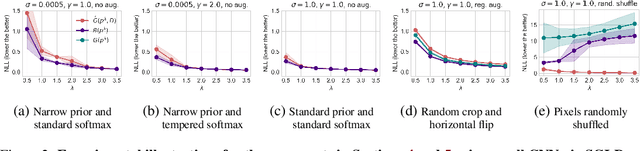
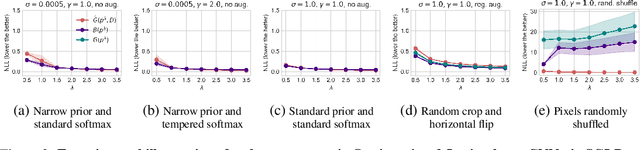
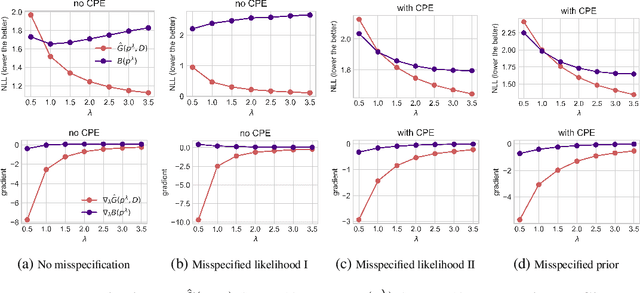
If there is no underfitting, there is no Cold Posterior Effect

The cold posterior effect (CPE) (Wenzel et al., 2020) in Bayesian deep learning shows that, for posteriors with a temperature $T<1$, the resulting posterior predictive could have better performances than the Bayesian posterior ($T=1$). As the Bayesian posterior is known to be optimal under perfect model specification, many recent works have studied the presence of CPE as a model misspecification problem, arising from the prior and/or from the likelihood function. In this work, we provide a more nuanced understanding of the CPE as we show that misspecification leads to CPE only when the resulting Bayesian posterior underfits. In fact, we theoretically show that if there is no underfitting, there is no CPE.

Understanding Generalization in the Interpolation Regime using the Rate Function

In this paper, we present a novel characterization of the smoothness of a model based on basic principles of Large Deviation Theory. In contrast to prior work, where the smoothness of a model is normally characterized by a real value (e.g., the weights' norm), we show that smoothness can be described by a simple real-valued function. Based on this concept of smoothness, we propose an unifying theoretical explanation of why some interpolators generalize remarkably well and why a wide range of modern learning techniques (i.e., stochastic gradient descent, $\ell_2$-norm regularization, data augmentation, invariant architectures, and overparameterization) are able to find them. The emergent conclusion is that all these methods provide complimentary procedures that bias the optimizer to smoother interpolators, which, according to this theoretical analysis, are the ones with better generalization error.

Diversity and Generalization in Neural Network Ensembles

Ensembles are widely used in machine learning and, usually, provide state-of-the-art performance in many prediction tasks. From the very beginning, the diversity of an ensemble has been identified as a key factor for the superior performance of these models. But the exact role that diversity plays in ensemble models is poorly understood, specially in the context of neural networks. In this work, we combine and expand previously published results in a theoretically sound framework that describes the relationship between diversity and ensemble performance for a wide range of ensemble methods. More precisely, we provide sound answers to the following questions: how to measure diversity, how diversity relates to the generalization error of an ensemble, and how diversity is promoted by neural network ensemble algorithms. This analysis covers three widely used loss functions, namely, the squared loss, the cross-entropy loss, and the 0-1 loss; and two widely used model combination strategies, namely, model averaging and weighted majority vote. We empirically validate this theoretical analysis with neural network ensembles.

Chebyshev-Cantelli PAC-Bayes-Bennett Inequality for the Weighted Majority Vote

We present a new second-order oracle bound for the expected risk of a weighted majority vote. The bound is based on a novel parametric form of the Chebyshev-Cantelli inequality (a.k.a.\ one-sided Chebyshev's), which is amenable to efficient minimization. The new form resolves the optimization challenge faced by prior oracle bounds based on the Chebyshev-Cantelli inequality, the C-bounds [Germain et al., 2015], and, at the same time, it improves on the oracle bound based on second order Markov's inequality introduced by Masegosa et al. [2020]. We also derive the PAC-Bayes-Bennett inequality, which we use for empirical estimation of the oracle bound. The PAC-Bayes-Bennett inequality improves on the PAC-Bayes-Bernstein inequality by Seldin et al. [2012]. We provide an empirical evaluation demonstrating that the new bounds can improve on the work by Masegosa et al. [2020]. Both the parametric form of the Chebyshev-Cantelli inequality and the PAC-Bayes-Bennett inequality may be of independent interest for the study of concentration of measure in other domains.

InferPy: Probabilistic Modeling with Deep Neural Networks Made Easy

InferPy is a Python package for probabilistic modeling with deep neural networks. InferPy defines a user-friendly API which trades-off model complexity with ease of use, unlike other libraries whose focus is on dealing with very general probabilistic models at the cost of having a more complex API. In particular, InferPy allows to define, learn and evaluate general hierarchical probabilistic models containing deep neural networks in a compact and simple way. InferPy is built on top of Tensorflow, Edward2 and Keras.

Probabilistic Models with Deep Neural Networks

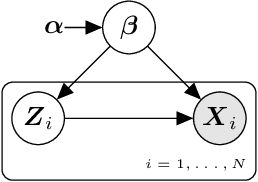
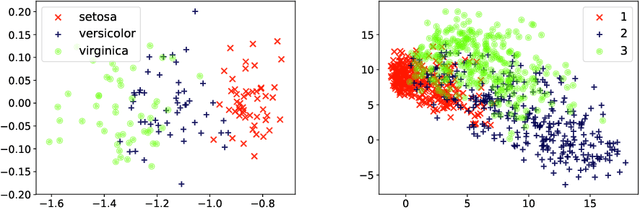
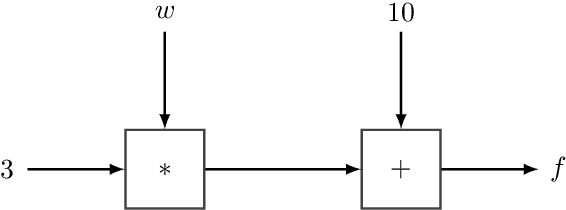
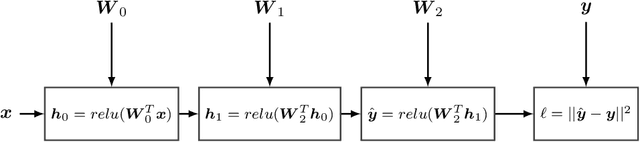
Recent advances in statistical inference have significantly expanded the toolbox of probabilistic modeling. Historically, probabilistic modeling has been constrained to (i) very restricted model classes where exact or approximate probabilistic inference were feasible, and (ii) small or medium-sized data sets which fit within the main memory of the computer. However, developments in variational inference, a general form of approximate probabilistic inference originated in statistical physics, are allowing probabilistic modeling to overcome these restrictions: (i) Approximate probabilistic inference is now possible over a broad class of probabilistic models containing a large number of parameters, and (ii) scalable inference methods based on stochastic gradient descent and distributed computation engines allow to apply probabilistic modeling over massive data sets. One important practical consequence of these advances is the possibility to include deep neural networks within a probabilistic model to capture complex non-linear stochastic relationships between random variables. These advances in conjunction with the release of novel probabilistic modeling toolboxes have greatly expanded the scope of application of probabilistic models, and allow these models to take advantage of the recent strides made by the deep learning community. In this paper we review the main concepts, methods and tools needed to use deep neural networks within a probabilistic modeling framework.

AMIDST: a Java Toolbox for Scalable Probabilistic Machine Learning

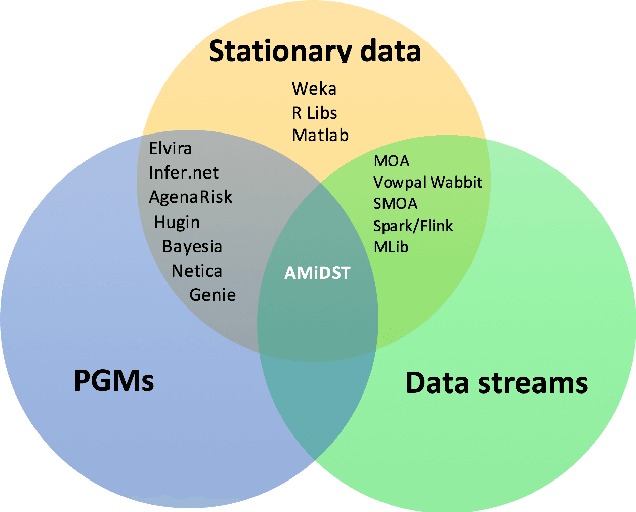
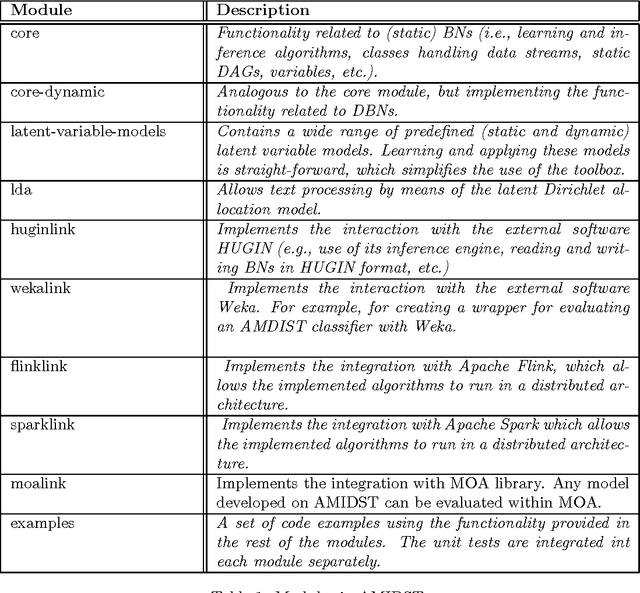
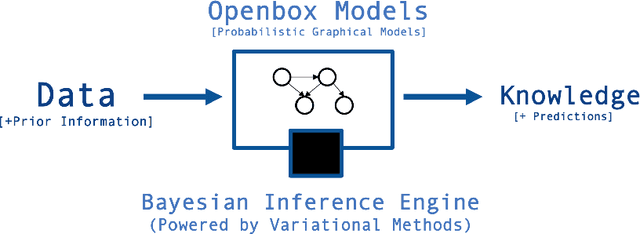
The AMIDST Toolbox is a software for scalable probabilistic machine learning with a spe- cial focus on (massive) streaming data. The toolbox supports a flexible modeling language based on probabilistic graphical models with latent variables and temporal dependencies. The specified models can be learnt from large data sets using parallel or distributed implementa- tions of Bayesian learning algorithms for either streaming or batch data. These algorithms are based on a flexible variational message passing scheme, which supports discrete and continu- ous variables from a wide range of probability distributions. AMIDST also leverages existing functionality and algorithms by interfacing to software tools such as Flink, Spark, MOA, Weka, R and HUGIN. AMIDST is an open source toolbox written in Java and available at http://www.amidsttoolbox.com under the Apache Software License version 2.0.