If there is no underfitting, there is no Cold Posterior Effect
Paper and Code
Oct 02, 2023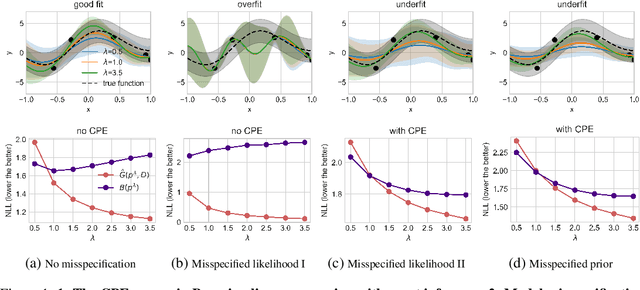
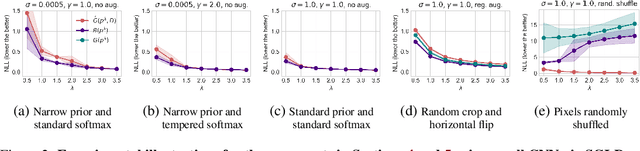
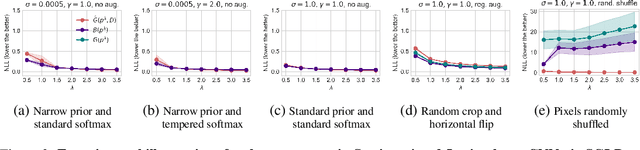
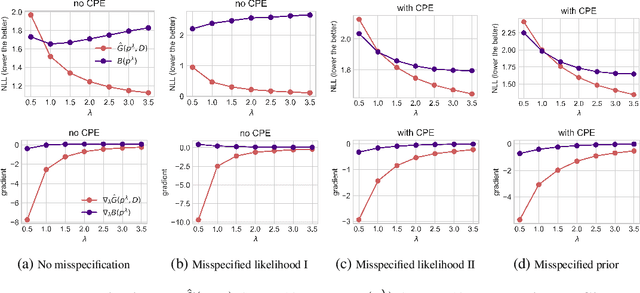
The cold posterior effect (CPE) (Wenzel et al., 2020) in Bayesian deep learning shows that, for posteriors with a temperature $T<1$, the resulting posterior predictive could have better performances than the Bayesian posterior ($T=1$). As the Bayesian posterior is known to be optimal under perfect model specification, many recent works have studied the presence of CPE as a model misspecification problem, arising from the prior and/or from the likelihood function. In this work, we provide a more nuanced understanding of the CPE as we show that misspecification leads to CPE only when the resulting Bayesian posterior underfits. In fact, we theoretically show that if there is no underfitting, there is no CPE.
* 9 pages, 3 figures, ICLR 2024
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge