Exploring Pessimism and Optimism Dynamics in Deep Reinforcement Learning

Off-policy actor-critic algorithms have shown promise in deep reinforcement learning for continuous control tasks. Their success largely stems from leveraging pessimistic state-action value function updates, which effectively address function approximation errors and improve performance. However, such pessimism can lead to under-exploration, constraining the agent's ability to explore/refine its policies. Conversely, optimism can counteract under-exploration, but it also carries the risk of excessive risk-taking and poor convergence if not properly balanced. Based on these insights, we introduce Utility Soft Actor-Critic (USAC), a novel framework within the actor-critic paradigm that enables independent control over the degree of pessimism/optimism for both the actor and the critic via interpretable parameters. USAC adapts its exploration strategy based on the uncertainty of critics through a utility function that allows us to balance between pessimism and optimism separately. By going beyond binary choices of optimism and pessimism, USAC represents a significant step towards achieving balance within off-policy actor-critic algorithms. Our experiments across various continuous control problems show that the degree of pessimism or optimism depends on the nature of the task. Furthermore, we demonstrate that USAC can outperform state-of-the-art algorithms for appropriately configured pessimism/optimism parameters.

Recursive PAC-Bayes: A Frequentist Approach to Sequential Prior Updates with No Information Loss

PAC-Bayesian analysis is a frequentist framework for incorporating prior knowledge into learning. It was inspired by Bayesian learning, which allows sequential data processing and naturally turns posteriors from one processing step into priors for the next. However, despite two and a half decades of research, the ability to update priors sequentially without losing confidence information along the way remained elusive for PAC-Bayes. While PAC-Bayes allows construction of data-informed priors, the final confidence intervals depend only on the number of points that were not used for the construction of the prior, whereas confidence information in the prior, which is related to the number of points used to construct the prior, is lost. This limits the possibility and benefit of sequential prior updates, because the final bounds depend only on the size of the final batch. We present a novel and, in retrospect, surprisingly simple and powerful PAC-Bayesian procedure that allows sequential prior updates with no information loss. The procedure is based on a novel decomposition of the expected loss of randomized classifiers. The decomposition rewrites the loss of the posterior as an excess loss relative to a downscaled loss of the prior plus the downscaled loss of the prior, which is bounded recursively. As a side result, we also present a generalization of the split-kl and PAC-Bayes-split-kl inequalities to discrete random variables, which we use for bounding the excess losses, and which can be of independent interest. In empirical evaluation the new procedure significantly outperforms state-of-the-art.

Probabilistic Actor-Critic: Learning to Explore with PAC-Bayes Uncertainty

We introduce Probabilistic Actor-Critic (PAC), a novel reinforcement learning algorithm with improved continuous control performance thanks to its ability to mitigate the exploration-exploitation trade-off. PAC achieves this by seamlessly integrating stochastic policies and critics, creating a dynamic synergy between the estimation of critic uncertainty and actor training. The key contribution of our PAC algorithm is that it explicitly models and infers epistemic uncertainty in the critic through Probably Approximately Correct-Bayesian (PAC-Bayes) analysis. This incorporation of critic uncertainty enables PAC to adapt its exploration strategy as it learns, guiding the actor's decision-making process. PAC compares favorably against fixed or pre-scheduled exploration schemes of the prior art. The synergy between stochastic policies and critics, guided by PAC-Bayes analysis, represents a fundamental step towards a more adaptive and effective exploration strategy in deep reinforcement learning. We report empirical evaluations demonstrating PAC's enhanced stability and improved performance over the state of the art in diverse continuous control problems.

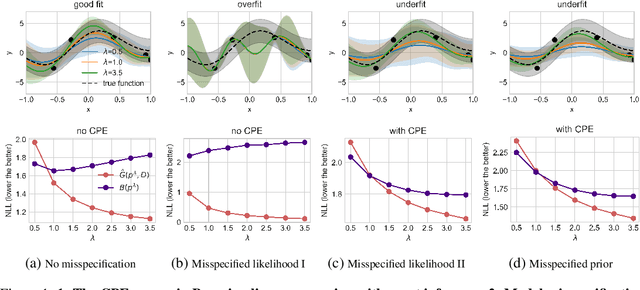
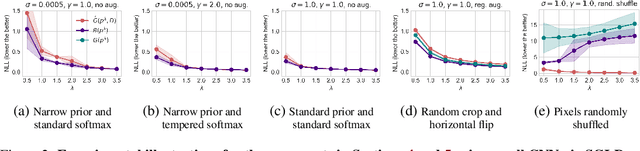
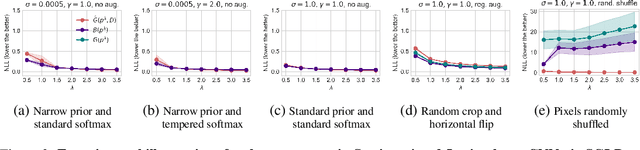
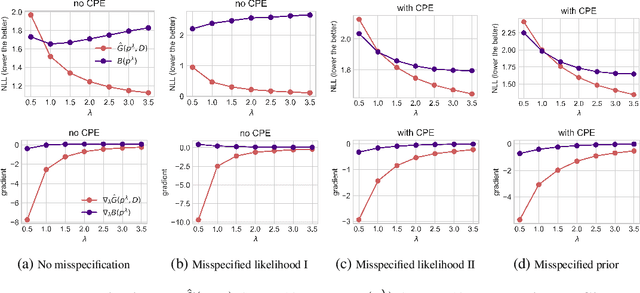
If there is no underfitting, there is no Cold Posterior Effect

The cold posterior effect (CPE) (Wenzel et al., 2020) in Bayesian deep learning shows that, for posteriors with a temperature $T<1$, the resulting posterior predictive could have better performances than the Bayesian posterior ($T=1$). As the Bayesian posterior is known to be optimal under perfect model specification, many recent works have studied the presence of CPE as a model misspecification problem, arising from the prior and/or from the likelihood function. In this work, we provide a more nuanced understanding of the CPE as we show that misspecification leads to CPE only when the resulting Bayesian posterior underfits. In fact, we theoretically show that if there is no underfitting, there is no CPE.

Split-kl and PAC-Bayes-split-kl Inequalities

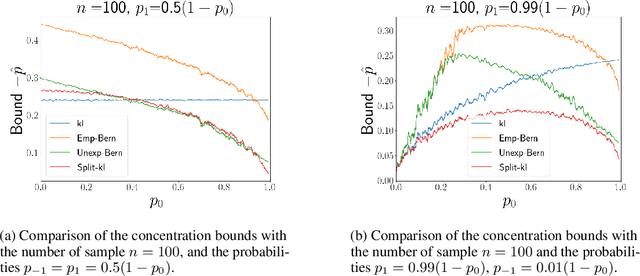
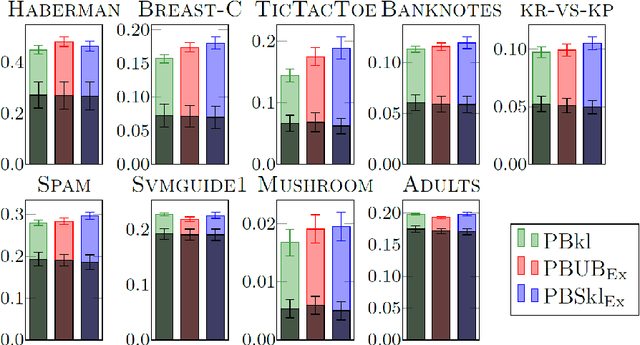
We present a new concentration of measure inequality for sums of independent bounded random variables, which we name a split-kl inequality. The inequality combines the combinatorial power of the kl inequality with ability to exploit low variance. While for Bernoulli random variables the kl inequality is tighter than the Empirical Bernstein, for random variables taking values inside a bounded interval and having low variance the Empirical Bernstein inequality is tighter than the kl. The proposed split-kl inequality yields the best of both worlds. We discuss an application of the split-kl inequality to bounding excess losses. We also derive a PAC-Bayes-split-kl inequality and use a synthetic example and several UCI datasets to compare it with the PAC-Bayes-kl, PAC-Bayes Empirical Bernstein, PAC-Bayes Unexpected Bernstein, and PAC-Bayes Empirical Bennett inequalities.

Chebyshev-Cantelli PAC-Bayes-Bennett Inequality for the Weighted Majority Vote

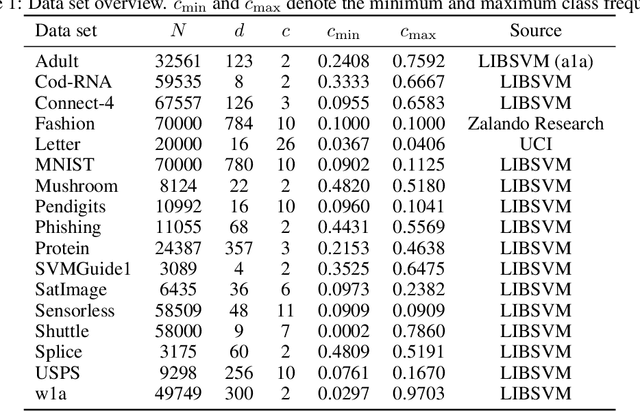
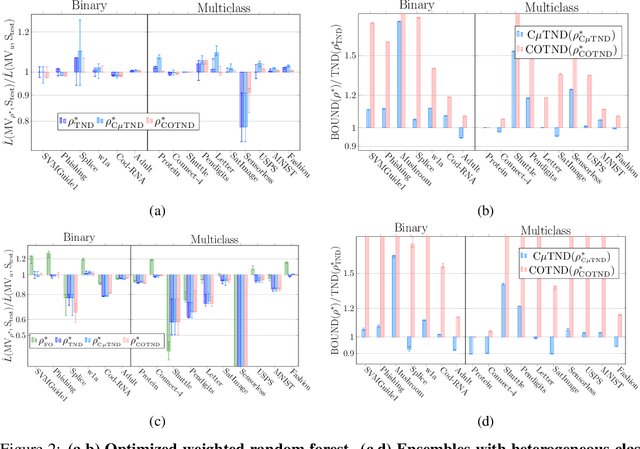
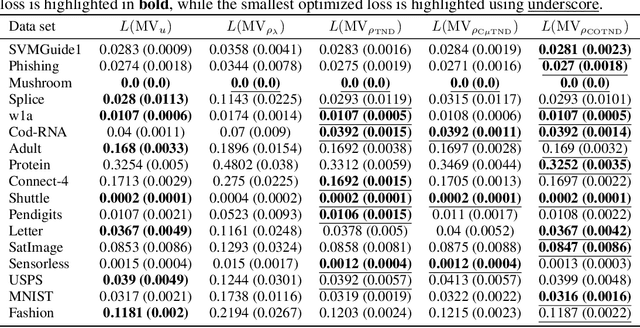
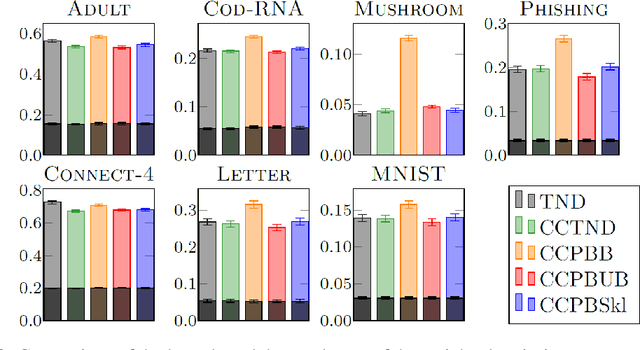
We present a new second-order oracle bound for the expected risk of a weighted majority vote. The bound is based on a novel parametric form of the Chebyshev-Cantelli inequality (a.k.a.\ one-sided Chebyshev's), which is amenable to efficient minimization. The new form resolves the optimization challenge faced by prior oracle bounds based on the Chebyshev-Cantelli inequality, the C-bounds [Germain et al., 2015], and, at the same time, it improves on the oracle bound based on second order Markov's inequality introduced by Masegosa et al. [2020]. We also derive the PAC-Bayes-Bennett inequality, which we use for empirical estimation of the oracle bound. The PAC-Bayes-Bennett inequality improves on the PAC-Bayes-Bernstein inequality by Seldin et al. [2012]. We provide an empirical evaluation demonstrating that the new bounds can improve on the work by Masegosa et al. [2020]. Both the parametric form of the Chebyshev-Cantelli inequality and the PAC-Bayes-Bennett inequality may be of independent interest for the study of concentration of measure in other domains.