Revisiting K-mer Profile for Effective and Scalable Genome Representation Learning

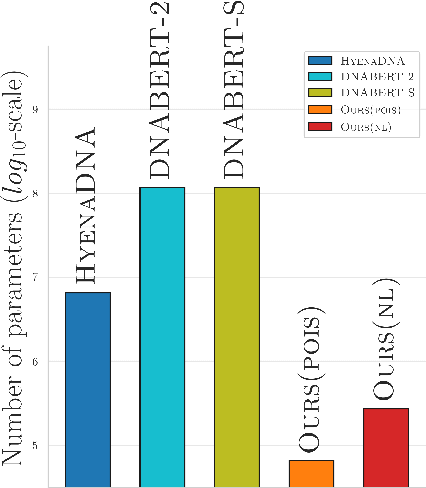
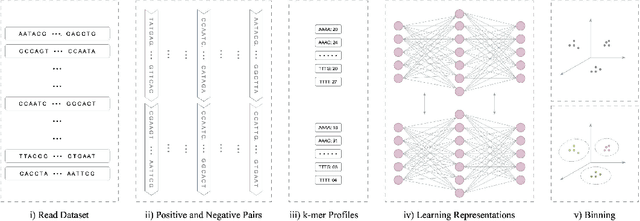
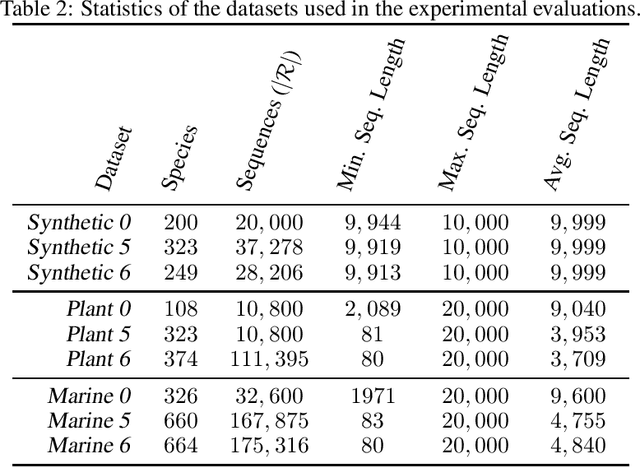
Obtaining effective representations of DNA sequences is crucial for genome analysis. Metagenomic binning, for instance, relies on genome representations to cluster complex mixtures of DNA fragments from biological samples with the aim of determining their microbial compositions. In this paper, we revisit k-mer-based representations of genomes and provide a theoretical analysis of their use in representation learning. Based on the analysis, we propose a lightweight and scalable model for performing metagenomic binning at the genome read level, relying only on the k-mer compositions of the DNA fragments. We compare the model to recent genome foundation models and demonstrate that while the models are comparable in performance, the proposed model is significantly more effective in terms of scalability, a crucial aspect for performing metagenomic binning of real-world datasets.

Learning from i.i.d. data under model miss-specification

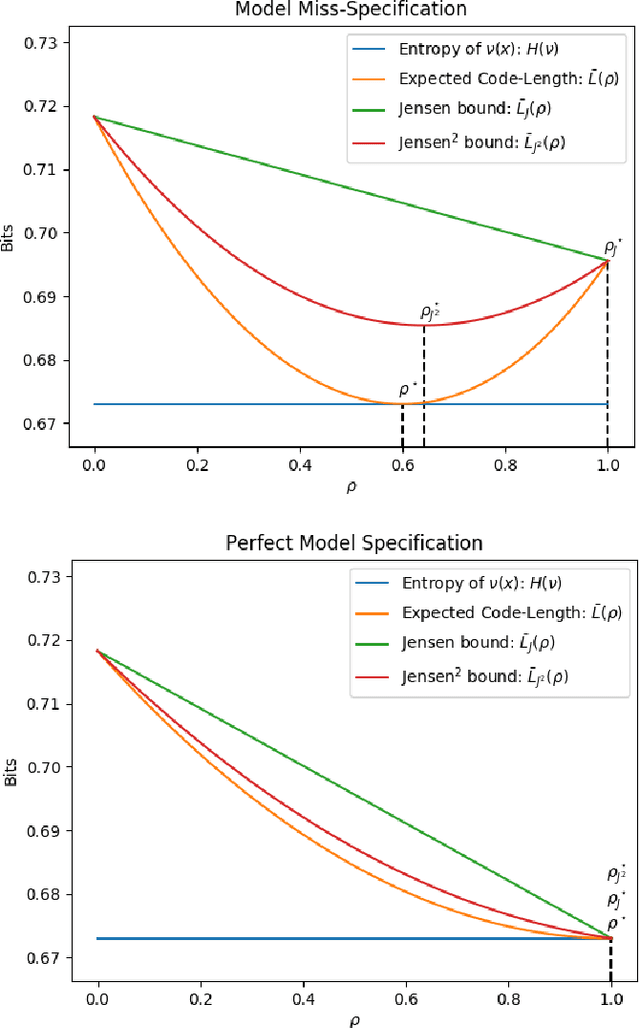
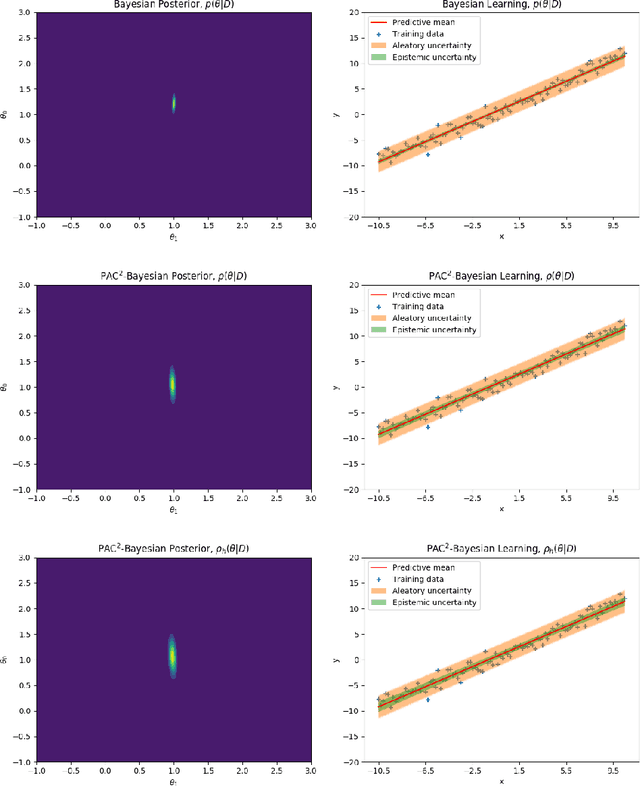
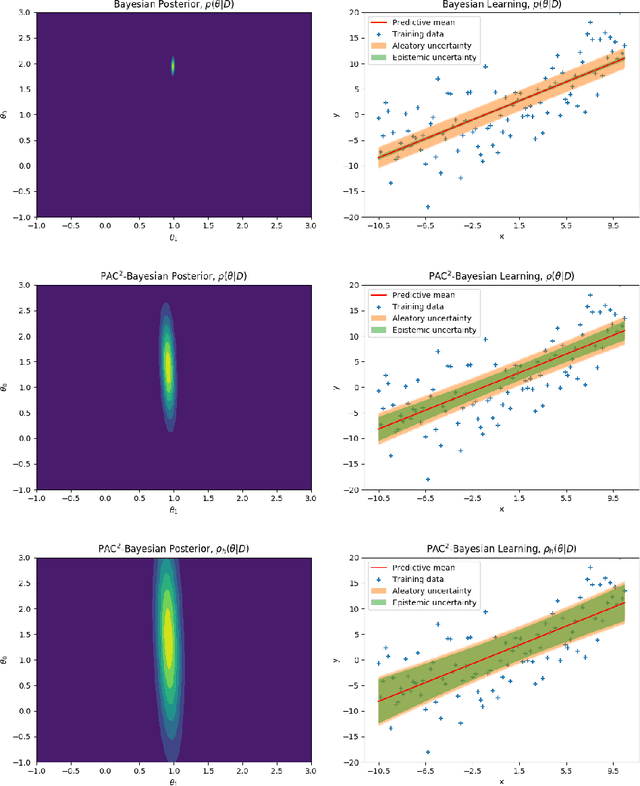
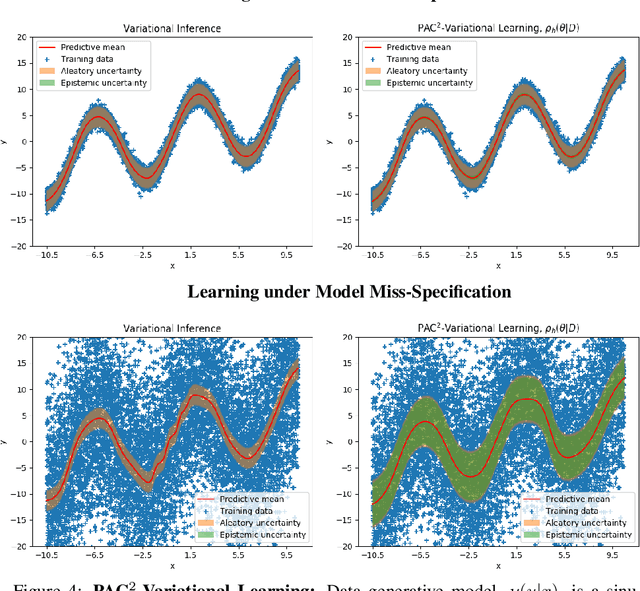
This paper introduces a new approach to learning from i.i.d. data under model miss-specification. This approach casts the problem of learning as minimizing the expected code-length of a Bayesian mixture code. To solve this problem, we build on PAC-Bayes bounds, information theory and a new family of second-order Jensen bounds. The key insight of this paper is that the use of the standard (first-order) Jensen bounds in learning is suboptimal when our model class is miss-specified (i.e. it does not contain the data generating distribution). As a consequence of this insight, this work provides strong theoretical arguments explaining why the Bayesian posterior is not optimal for making predictions that generalize under model miss-specification because the Bayesian posterior is directly related to the use of first-order Jensen bounds. We then argue for the use of second-order Jensen bounds, which leads to new families of learning algorithms. In this work, we introduce novel variational and ensemble learning methods based on the minimization of a novel family of second-order PAC-Bayes bounds over the expected code-length of a Bayesian mixture code. Using this new framework, we also provide novel hypotheses of why parameters in a flat minimum generalize better than parameters in a sharp minimum.

Probabilistic Graphical Models on Multi-Core CPUs using Java 8

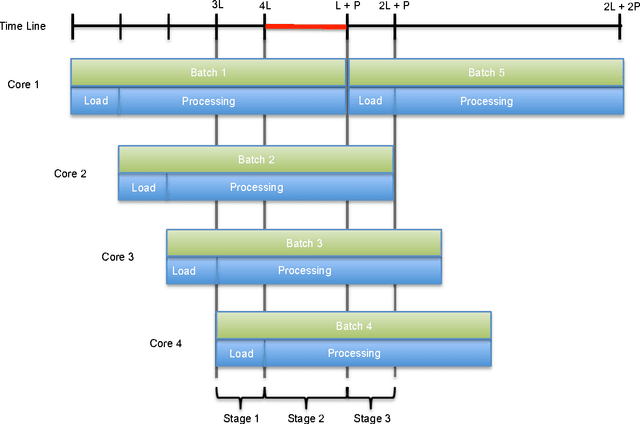
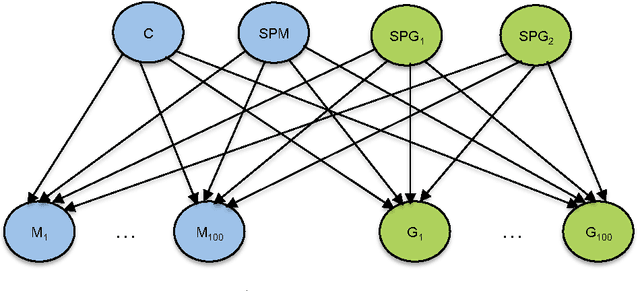
In this paper, we discuss software design issues related to the development of parallel computational intelligence algorithms on multi-core CPUs, using the new Java 8 functional programming features. In particular, we focus on probabilistic graphical models (PGMs) and present the parallelisation of a collection of algorithms that deal with inference and learning of PGMs from data. Namely, maximum likelihood estimation, importance sampling, and greedy search for solving combinatorial optimisation problems. Through these concrete examples, we tackle the problem of defining efficient data structures for PGMs and parallel processing of same-size batches of data sets using Java 8 features. We also provide straightforward techniques to code parallel algorithms that seamlessly exploit multi-core processors. The experimental analysis, carried out using our open source AMIDST (Analysis of MassIve Data STreams) Java toolbox, shows the merits of the proposed solutions.

Stochastic Discriminative EM

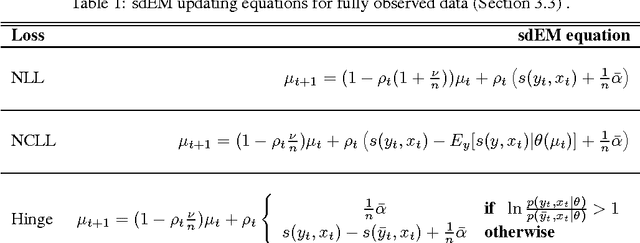
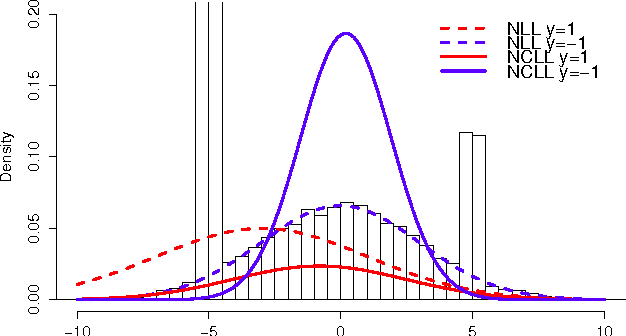
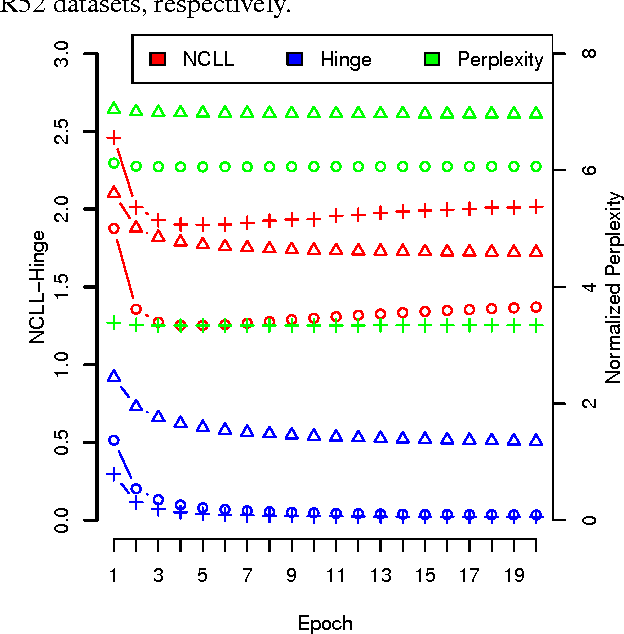
Stochastic discriminative EM (sdEM) is an online-EM-type algorithm for discriminative training of probabilistic generative models belonging to the exponential family. In this work, we introduce and justify this algorithm as a stochastic natural gradient descent method, i.e. a method which accounts for the information geometry in the parameter space of the statistical model. We show how this learning algorithm can be used to train probabilistic generative models by minimizing different discriminative loss functions, such as the negative conditional log-likelihood and the Hinge loss. The resulting models trained by sdEM are always generative (i.e. they define a joint probability distribution) and, in consequence, allows to deal with missing data and latent variables in a principled way either when being learned or when making predictions. The performance of this method is illustrated by several text classification problems for which a multinomial naive Bayes and a latent Dirichlet allocation based classifier are learned using different discriminative loss functions.