Revisiting K-mer Profile for Effective and Scalable Genome Representation Learning

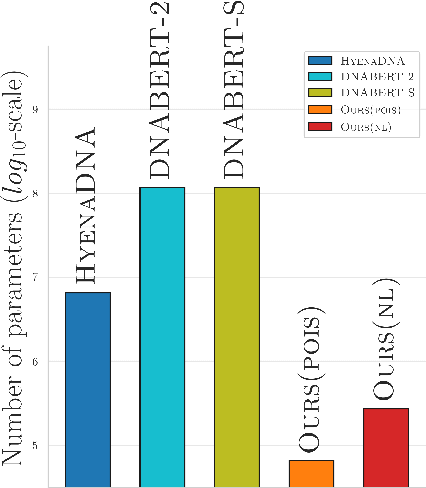
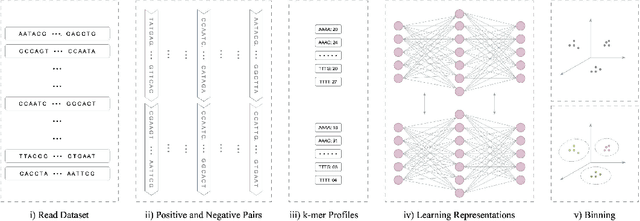
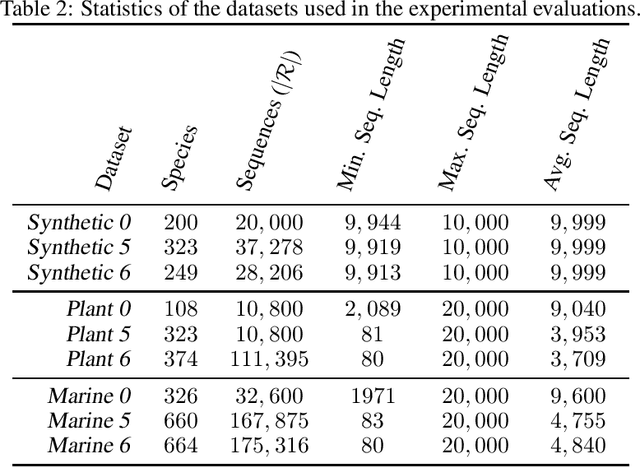
Obtaining effective representations of DNA sequences is crucial for genome analysis. Metagenomic binning, for instance, relies on genome representations to cluster complex mixtures of DNA fragments from biological samples with the aim of determining their microbial compositions. In this paper, we revisit k-mer-based representations of genomes and provide a theoretical analysis of their use in representation learning. Based on the analysis, we propose a lightweight and scalable model for performing metagenomic binning at the genome read level, relying only on the k-mer compositions of the DNA fragments. We compare the model to recent genome foundation models and demonstrate that while the models are comparable in performance, the proposed model is significantly more effective in terms of scalability, a crucial aspect for performing metagenomic binning of real-world datasets.

Probabilistic Models with Deep Neural Networks

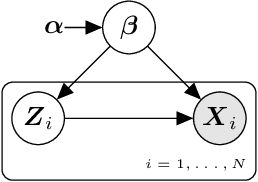
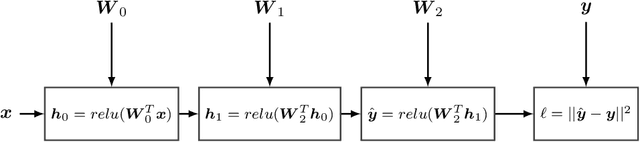
Recent advances in statistical inference have significantly expanded the toolbox of probabilistic modeling. Historically, probabilistic modeling has been constrained to (i) very restricted model classes where exact or approximate probabilistic inference were feasible, and (ii) small or medium-sized data sets which fit within the main memory of the computer. However, developments in variational inference, a general form of approximate probabilistic inference originated in statistical physics, are allowing probabilistic modeling to overcome these restrictions: (i) Approximate probabilistic inference is now possible over a broad class of probabilistic models containing a large number of parameters, and (ii) scalable inference methods based on stochastic gradient descent and distributed computation engines allow to apply probabilistic modeling over massive data sets. One important practical consequence of these advances is the possibility to include deep neural networks within a probabilistic model to capture complex non-linear stochastic relationships between random variables. These advances in conjunction with the release of novel probabilistic modeling toolboxes have greatly expanded the scope of application of probabilistic models, and allow these models to take advantage of the recent strides made by the deep learning community. In this paper we review the main concepts, methods and tools needed to use deep neural networks within a probabilistic modeling framework.

Bayesian Models of Data Streams with Hierarchical Power Priors

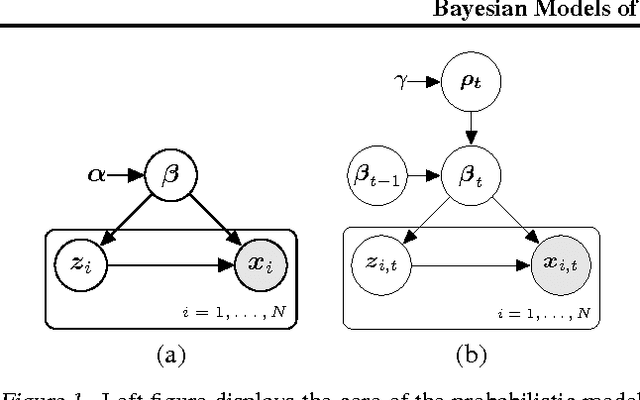
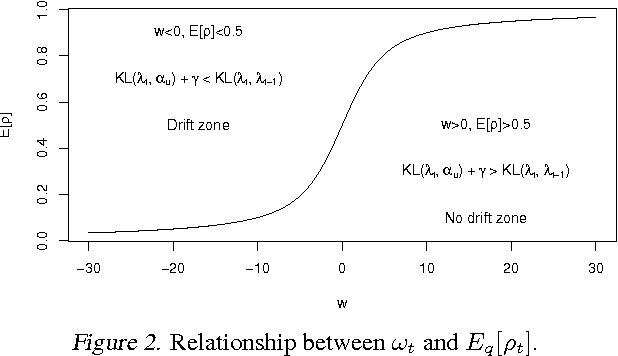
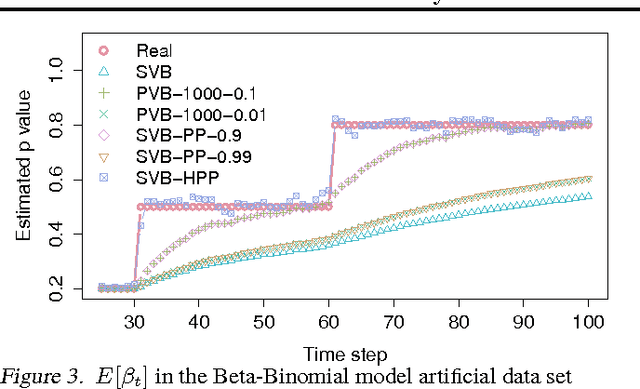
Making inferences from data streams is a pervasive problem in many modern data analysis applications. But it requires to address the problem of continuous model updating and adapt to changes or drifts in the underlying data generating distribution. In this paper, we approach these problems from a Bayesian perspective covering general conjugate exponential models. Our proposal makes use of non-conjugate hierarchical priors to explicitly model temporal changes of the model parameters. We also derive a novel variational inference scheme which overcomes the use of non-conjugate priors while maintaining the computational efficiency of variational methods over conjugate models. The approach is validated on three real data sets over three latent variable models.

AMIDST: a Java Toolbox for Scalable Probabilistic Machine Learning

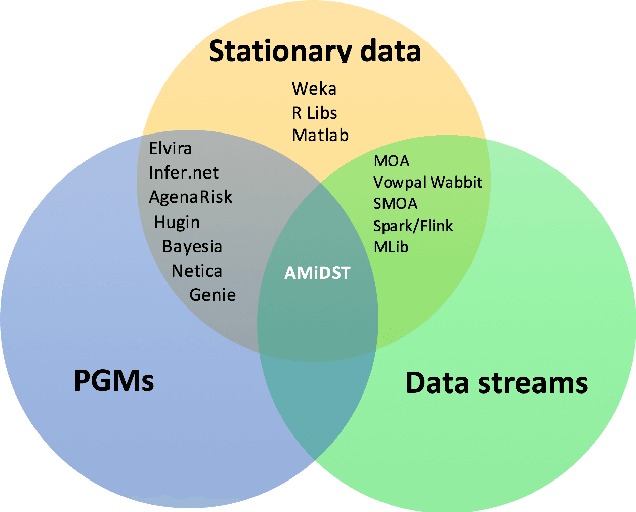
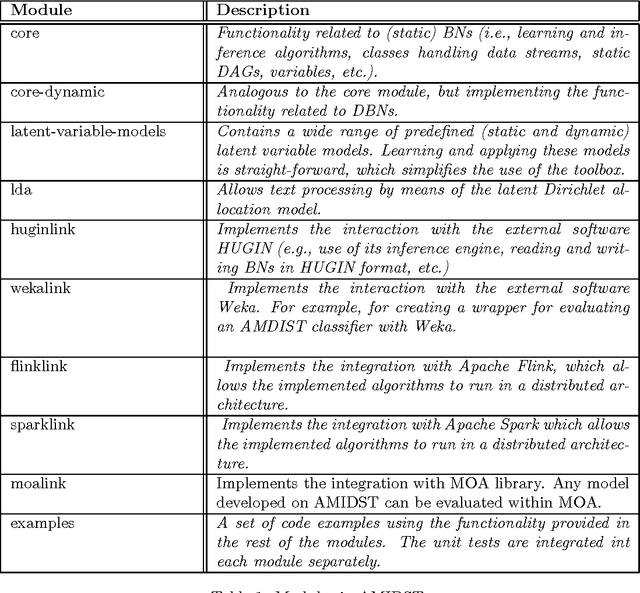
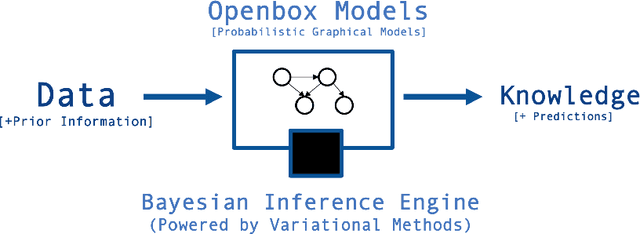
The AMIDST Toolbox is a software for scalable probabilistic machine learning with a spe- cial focus on (massive) streaming data. The toolbox supports a flexible modeling language based on probabilistic graphical models with latent variables and temporal dependencies. The specified models can be learnt from large data sets using parallel or distributed implementa- tions of Bayesian learning algorithms for either streaming or batch data. These algorithms are based on a flexible variational message passing scheme, which supports discrete and continu- ous variables from a wide range of probability distributions. AMIDST also leverages existing functionality and algorithms by interfacing to software tools such as Flink, Spark, MOA, Weka, R and HUGIN. AMIDST is an open source toolbox written in Java and available at http://www.amidsttoolbox.com under the Apache Software License version 2.0.

Welldefined Decision Scenarios

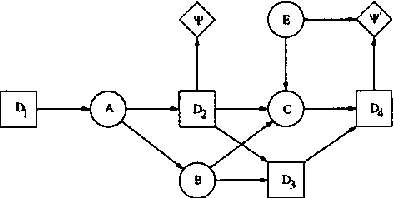
Influence diagrams serve as a powerful tool for modelling symmetric decision problems. When solving an influence diagram we determine a set of strategies for the decisions involved. A strategy for a decision variable is in principle a function over its past. However, some of the past may be irrelevant for the decision, and for computational reasons it is important not to deal with redundant variables in the strategies. We show that current methods (e.g. the "Decision Bayes-ball" algorithm by Shachter UAI98) do not determine the relevant past, and we present a complete algorithm. Actually, this paper takes a more general outset: When formulating a decision scenario as an influence diagram, a linear temporal ordering of the decisions variables is required. This constraint ensures that the decision scenario is welldefined. However, the structure of a decision scenario often yields certain decisions conditionally independent, and it is therefore unnecessary to impose a linear temporal ordering on the decisions. In this paper we deal with partial influence diagrams i.e. influence diagrams with only a partial temporal ordering specified. We present a set of conditions which are necessary and sufficient to ensure that a partial influence diagram is welldefined. These conditions are used as a basis for the construction of an algorithm for determining whether or not a partial influence diagram is welldefined.

Using ROBDDs for Inference in Bayesian Networks with Troubleshooting as an Example

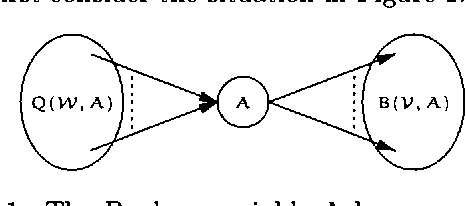
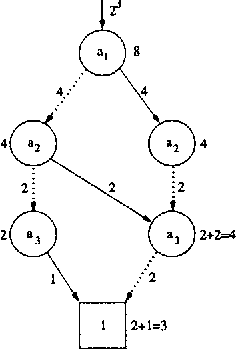
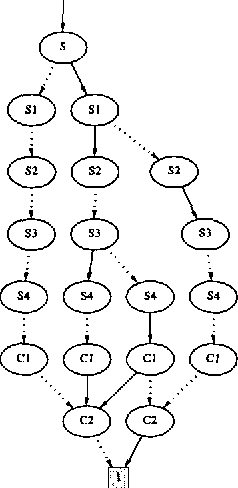
When using Bayesian networks for modelling the behavior of man-made machinery, it usually happens that a large part of the model is deterministic. For such Bayesian networks deterministic part of the model can be represented as a Boolean function, and a central part of belief updating reduces to the task of calculating the number of satisfying configurations in a Boolean function. In this paper we explore how advances in the calculation of Boolean functions can be adopted for belief updating, in particular within the context of troubleshooting. We present experimental results indicating a substantial speed-up compared to traditional junction tree propagation.

Representing and Solving Asymmetric Bayesian Decision Problems

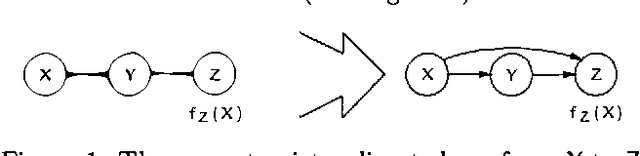
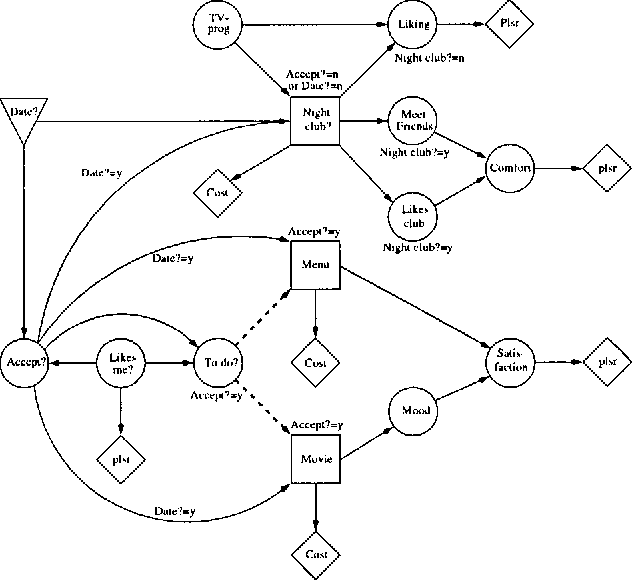
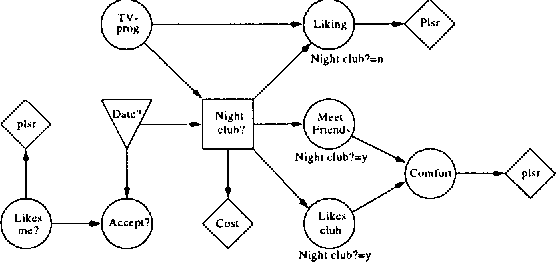
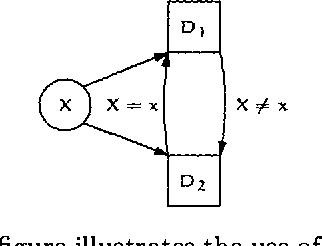
This paper deals with the representation and solution of asymmetric Bayesian decision problems. We present a formal framework, termed asymmetric influence diagrams, that is based on the influence diagram and allows an efficient representation of asymmetric decision problems. As opposed to existing frameworks, the asymmetric influece diagram primarily encodes asymmetry at the qualitative level and it can therefore be read directly from the model. We give an algorithm for solving asymmetric influence diagrams. The algorithm initially decomposes the asymmetric decision problem into a structure of symmetric subproblems organized as a tree. A solution to the decision problem can then be found by propagating from the leaves toward the root using existing evaluation methods to solve the sub-problems.

Learning Markov Decision Processes for Model Checking

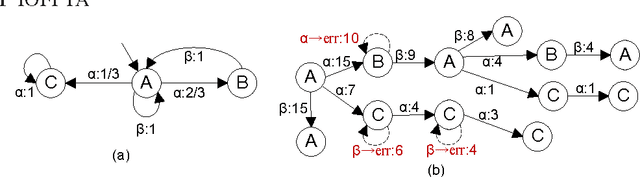
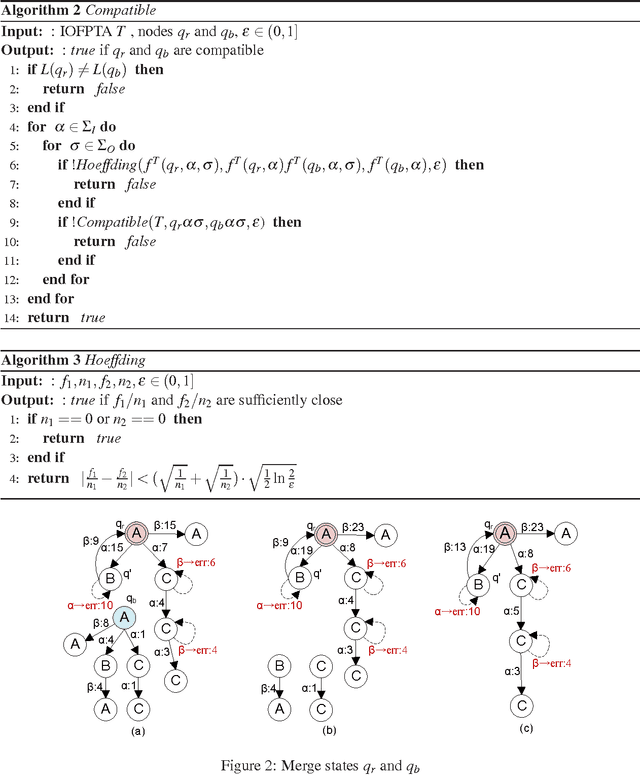
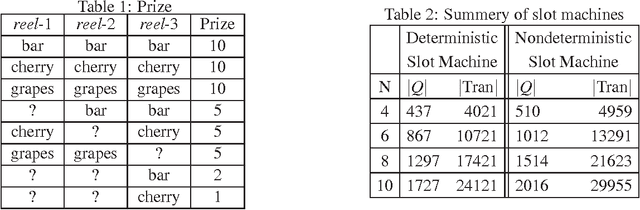
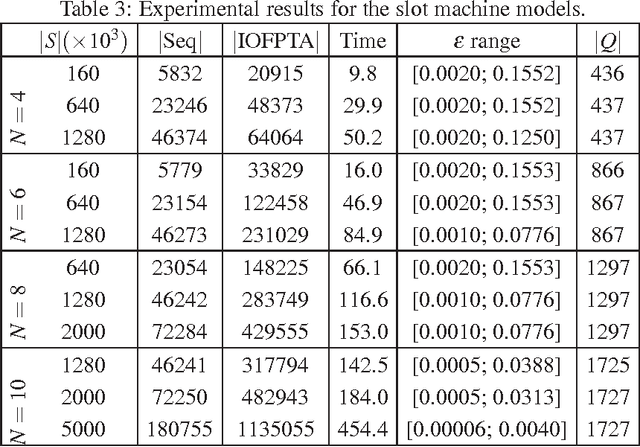
Constructing an accurate system model for formal model verification can be both resource demanding and time-consuming. To alleviate this shortcoming, algorithms have been proposed for automatically learning system models based on observed system behaviors. In this paper we extend the algorithm on learning probabilistic automata to reactive systems, where the observed system behavior is in the form of alternating sequences of inputs and outputs. We propose an algorithm for automatically learning a deterministic labeled Markov decision process model from the observed behavior of a reactive system. The proposed learning algorithm is adapted from algorithms for learning deterministic probabilistic finite automata, and extended to include both probabilistic and nondeterministic transitions. The algorithm is empirically analyzed and evaluated by learning system models of slot machines. The evaluation is performed by analyzing the probabilistic linear temporal logic properties of the system as well as by analyzing the schedulers, in particular the optimal schedulers, induced by the learned models.