Enhancing Safety Standards in Automated Systems Using Dynamic Bayesian Networks

Cut-in maneuvers in high-speed traffic pose critical challenges that can lead to abrupt braking and collisions, necessitating safe and efficient lane change strategies. We propose a Dynamic Bayesian Network (DBN) framework to integrate lateral evidence with safety assessment models, thereby predicting lane changes and ensuring safe cut-in maneuvers effectively. Our proposed framework comprises three key probabilistic hypotheses (lateral evidence, lateral safety, and longitudinal safety) that facilitate the decision-making process through dynamic data processing and assessments of vehicle positions, lateral velocities, relative distance, and Time-to-Collision (TTC) computations. The DBN model's performance compared with other conventional approaches demonstrates superior performance in crash reduction, especially in critical high-speed scenarios, while maintaining a competitive performance in low-speed scenarios. This paves the way for robust, scalable, and efficient safety validation in automated driving systems.

Bayesian Models of Data Streams with Hierarchical Power Priors

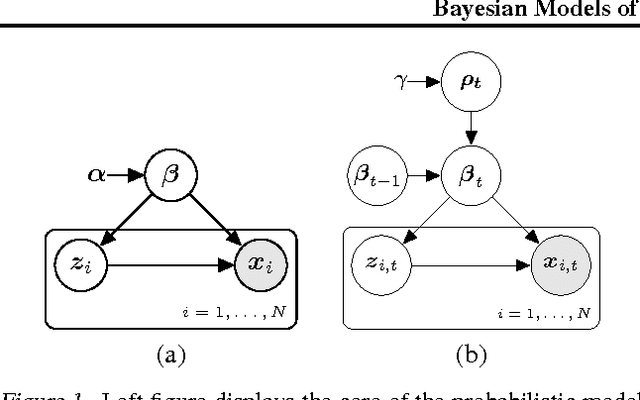
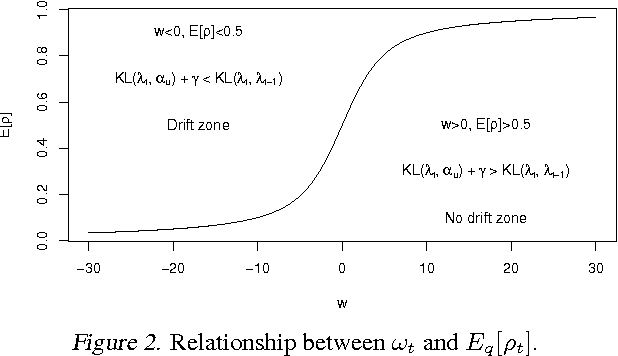
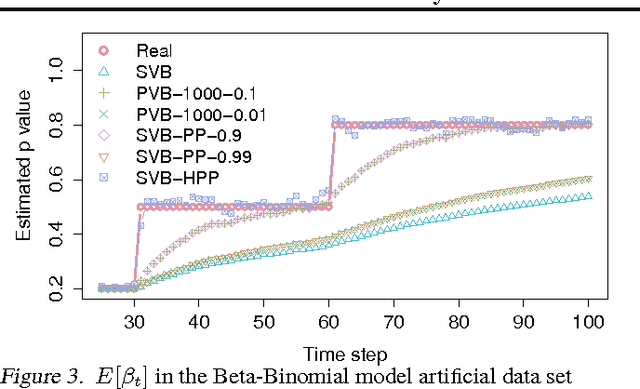
Making inferences from data streams is a pervasive problem in many modern data analysis applications. But it requires to address the problem of continuous model updating and adapt to changes or drifts in the underlying data generating distribution. In this paper, we approach these problems from a Bayesian perspective covering general conjugate exponential models. Our proposal makes use of non-conjugate hierarchical priors to explicitly model temporal changes of the model parameters. We also derive a novel variational inference scheme which overcomes the use of non-conjugate priors while maintaining the computational efficiency of variational methods over conjugate models. The approach is validated on three real data sets over three latent variable models.

AMIDST: a Java Toolbox for Scalable Probabilistic Machine Learning

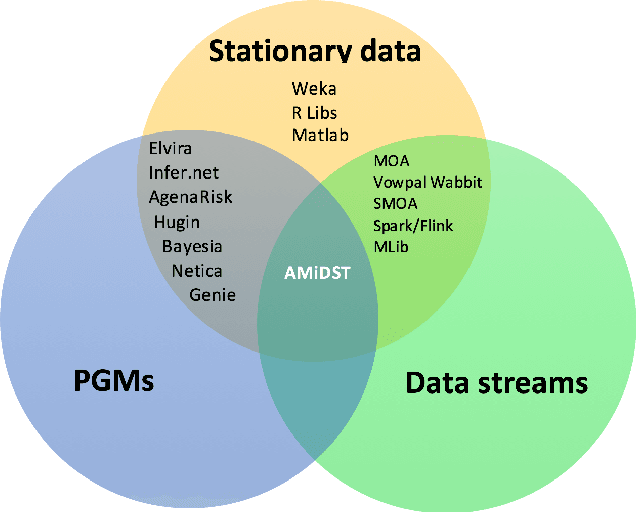
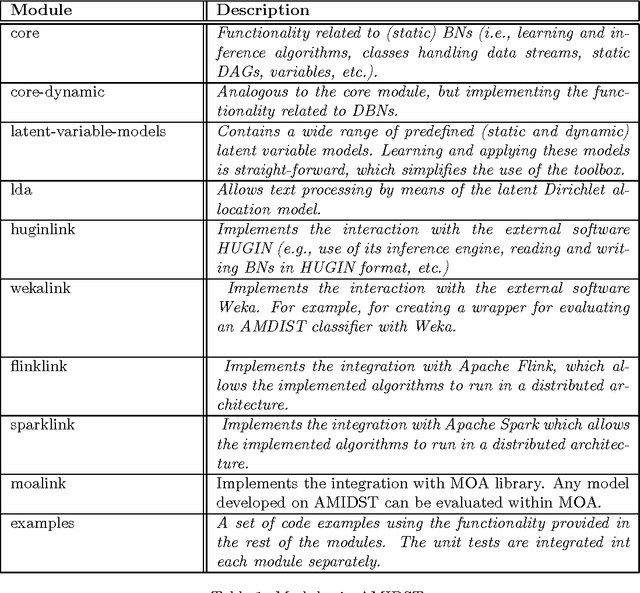
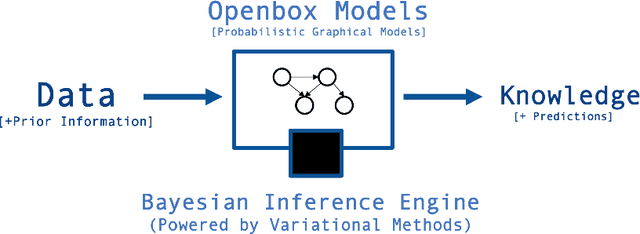
The AMIDST Toolbox is a software for scalable probabilistic machine learning with a spe- cial focus on (massive) streaming data. The toolbox supports a flexible modeling language based on probabilistic graphical models with latent variables and temporal dependencies. The specified models can be learnt from large data sets using parallel or distributed implementa- tions of Bayesian learning algorithms for either streaming or batch data. These algorithms are based on a flexible variational message passing scheme, which supports discrete and continu- ous variables from a wide range of probability distributions. AMIDST also leverages existing functionality and algorithms by interfacing to software tools such as Flink, Spark, MOA, Weka, R and HUGIN. AMIDST is an open source toolbox written in Java and available at http://www.amidsttoolbox.com under the Apache Software License version 2.0.

Lazy Propagation in Junction Trees

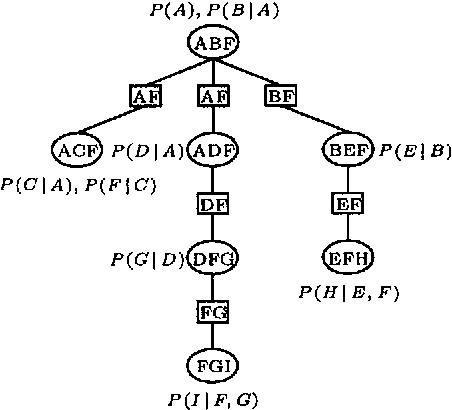
The efficiency of algorithms using secondary structures for probabilistic inference in Bayesian networks can be improved by exploiting independence relations induced by evidence and the direction of the links in the original network. In this paper we present an algorithm that on-line exploits independence relations induced by evidence and the direction of the links in the original network to reduce both time and space costs. Instead of multiplying the conditional probability distributions for the various cliques, we determine on-line which potentials to multiply when a message is to be produced. The performance improvement of the algorithm is emphasized through empirical evaluations involving large real world Bayesian networks, and we compare the method with the HUGIN and Shafer-Shenoy inference algorithms.

Lazy Evaluation of Symmetric Bayesian Decision Problems

Solving symmetric Bayesian decision problems is a computationally intensive task to perform regardless of the algorithm used. In this paper we propose a method for improving the efficiency of algorithms for solving Bayesian decision problems. The method is based on the principle of lazy evaluation - a principle recently shown to improve the efficiency of inference in Bayesian networks. The basic idea is to maintain decompositions of potentials and to postpone computations for as long as possible. The efficiency improvements obtained with the lazy evaluation based method is emphasized through examples. Finally, the lazy evaluation based method is compared with the hugin and valuation-based systems architectures for solving symmetric Bayesian decision problems.

Solving Influence Diagrams using HUGIN, Shafer-Shenoy and Lazy Propagation

In this paper we compare three different architectures for the evaluation of influence diagrams: HUGIN, Shafer-Shenoy, and Lazy Evaluation architecture. The computational complexity of the architectures are compared on the LImited Memory Influence Diagram (LIMID): a diagram where only the requiste information for the computation of the optimal policies are depicted. Because the requsite information is explicitly represented in the LIMID the evaluation can take advantage of it, and significant savings in computational can be obtained. In this paper we show how the obtained savings is considerably increased when the computations performed on the LIMID is according to the Lazy Evaluation scheme.

An Empirical Evaluation of Possible Variations of Lazy Propagation

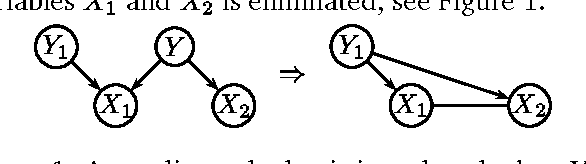
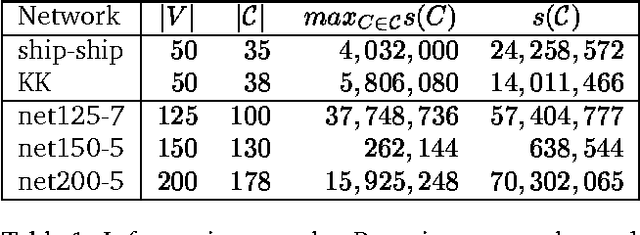
As real-world Bayesian networks continue to grow larger and more complex, it is important to investigate the possibilities for improving the performance of existing algorithms of probabilistic inference. Motivated by examples, we investigate the dependency of the performance of Lazy propagation on the message computation algorithm. We show how Symbolic Probabilistic Inference (SPI) and Arc-Reversal (AR) can be used for computation of clique to clique messages in the addition to the traditional use of Variable Elimination (VE). In addition, the paper resents the results of an empirical evaluation of the performance of Lazy propagation using VE, SPI, and AR as the message computation algorithm. The results of the empirical evaluation show that for most networks, the performance of inference did not depend on the choice of message computation algorithm, but for some randomly generated networks the choice had an impact on both space and time performance. In the cases where the choice had an impact, AR produced the best results.

A Differential Semantics of Lazy AR Propagation

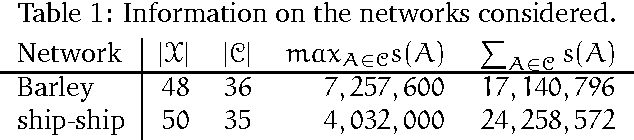
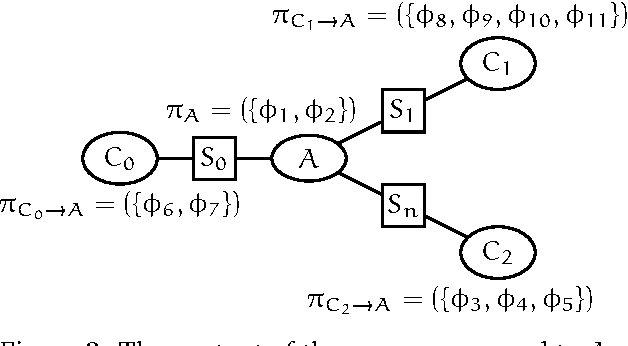
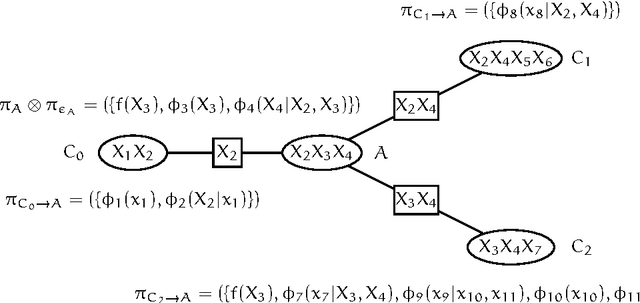
In this paper we present a differential semantics of Lazy AR Propagation (LARP) in discrete Bayesian networks. We describe how both single and multi dimensional partial derivatives of the evidence may easily be calculated from a junction tree in LARP equilibrium. We show that the simplicity of the calculations stems from the nature of LARP. Based on the differential semantics we describe how variable propagation in the LARP architecture may give access to additional partial derivatives. The cautious LARP (cLARP) scheme is derived to produce a flexible cLARP equilibrium that offers additional opportunities for calculating single and multidimensional partial derivatives of the evidence and subsets of the evidence from a single propagation. The results of an empirical evaluation illustrates how the access to a largely increased number of partial derivatives comes at a low computational cost.

Belief Update in CLG Bayesian Networks With Lazy Propagation

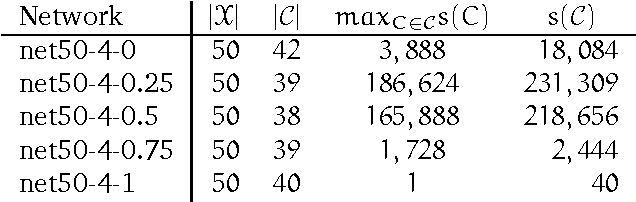
In recent years Bayesian networks (BNs) with a mixture of continuous and discrete variables have received an increasing level of attention. We present an architecture for exact belief update in Conditional Linear Gaussian BNs (CLG BNs). The architecture is an extension of lazy propagation using operations of Lauritzen & Jensen [6] and Cowell [2]. By decomposing clique and separator potentials into sets of factors, the proposed architecture takes advantage of independence and irrelevance properties induced by the structure of the graph and the evidence. The resulting benefits are illustrated by examples. Results of a preliminary empirical performance evaluation indicate a significant potential of the proposed architecture.