Analysis in HUGIN of Data Conflict

After a brief introduction to causal probabilistic networks and the HUGIN approach, the problem of conflicting data is discussed. A measure of conflict is defined, and it is used in the medical diagnostic system MUNIN. Finally, it is discussed how to distinguish between conflicting data and a rare case.

aHUGIN: A System Creating Adaptive Causal Probabilistic Networks

The paper describes aHUGIN, a tool for creating adaptive systems. aHUGIN is an extension of the HUGIN shell, and is based on the methods reported by Spiegelhalter and Lauritzen (1990a). The adaptive systems resulting from aHUGIN are able to adjust the C011ditional probabilities in the model. A short analysis of the adaptation task is given and the features of aHUGIN are described. Finally a session with experiments is reported and the results are discussed.

From Influence Diagrams to Junction Trees

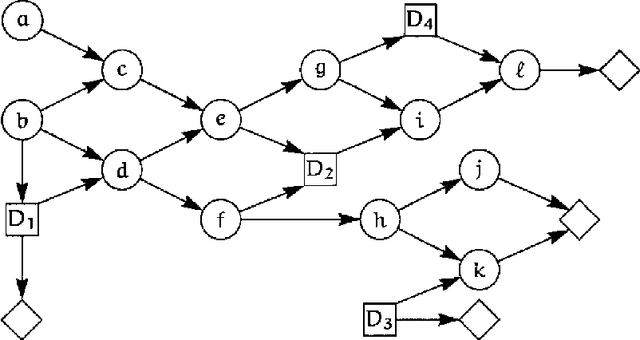
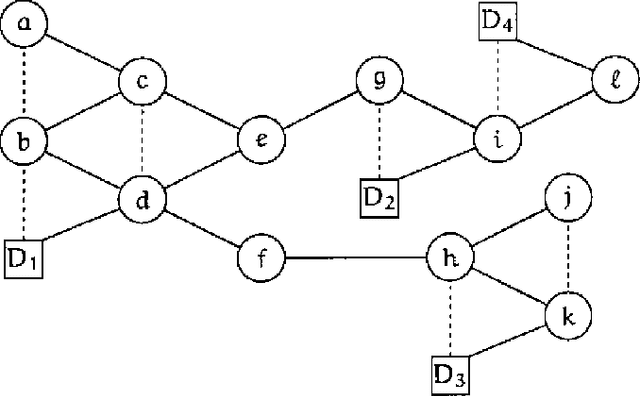
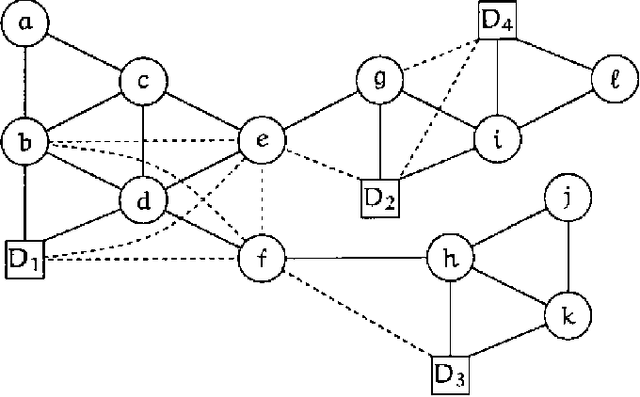
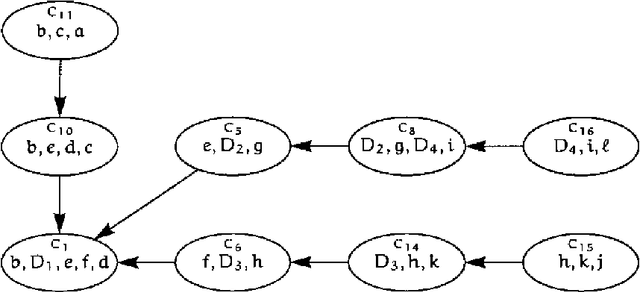
We present an approach to the solution of decision problems formulated as influence diagrams. This approach involves a special triangulation of the underlying graph, the construction of a junction tree with special properties, and a message passing algorithm operating on the junction tree for computation of expected utilities and optimal decision policies.

Optimal Junction Trees

The paper deals with optimality issues in connection with updating beliefs in networks. We address two processes: triangulation and construction of junction trees. In the first part, we give a simple algorithm for constructing an optimal junction tree from a triangulated network. In the second part, we argue that any exact method based on local calculations must either be less efficient than the junction tree method, or it has an optimality problem equivalent to that of triangulation.

Cautious Propagation in Bayesian Networks

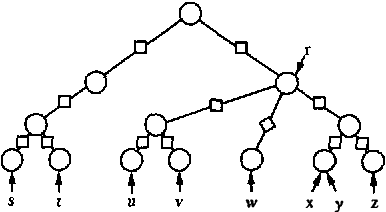
Consider the situation where some evidence e has been entered to a Bayesian network. When performing conflict analysis, sensitivity analysis, or when answering questions like "What if the finding on X had been y instead of x?" you need probabilities P (e'| h), where e' is a subset of e, and h is a configuration of a (possibly empty) set of variables. Cautious propagation is a modification of HUGIN propagation into a Shafer-Shenoy-like architecture. It is less efficient than HUGIN propagation; however, it provides easy access to P (e'| h) for a great deal of relevant subsets e'.

MIDAS - An Influence Diagram for Management of Mildew in Winter Wheat

We present a prototype of a decision support system for management of the fungal disease mildew in winter wheat. The prototype is based on an influence diagram which is used to determine the optimal time and dose of mildew treatments. This involves multiple decision opportunities over time, stochasticity, inaccurate information and incomplete knowledge. The paper describes the practical and theoretical problems encountered during the construction of the influence diagram, and also the experience with the prototype.

Myopic Value of Information in Influence Diagrams

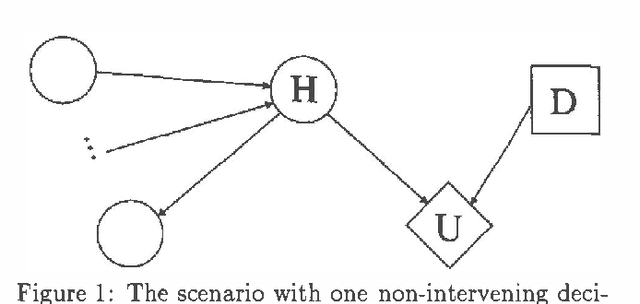
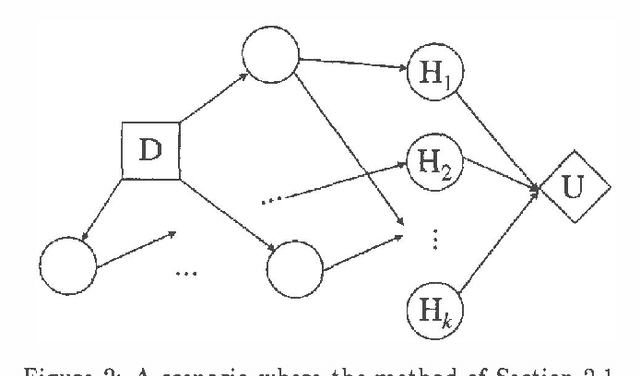
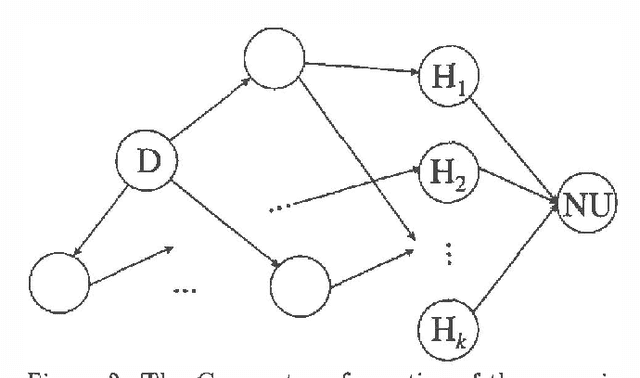
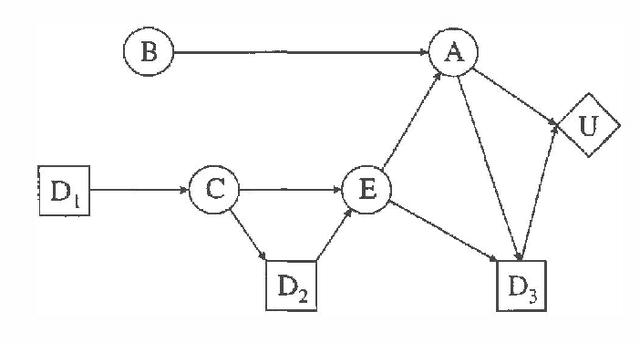
We present a method for calculation of myopic value of information in influence diagrams (Howard & Matheson, 1981) based on the strong junction tree framework (Jensen, Jensen & Dittmer, 1994). The difference in instantiation order in the influence diagrams is reflected in the corresponding junction trees by the order in which the chance nodes are marginalized. This order of marginalization can be changed by table expansion and in effect the same junction tree with expanded tables may be used for calculating the expected utility for scenarios with different instantiation order. We also compare our method to the classic method of modeling different instantiation orders in the same influence diagram.

Lazy Propagation in Junction Trees

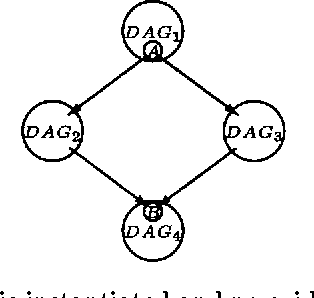
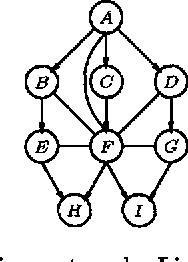
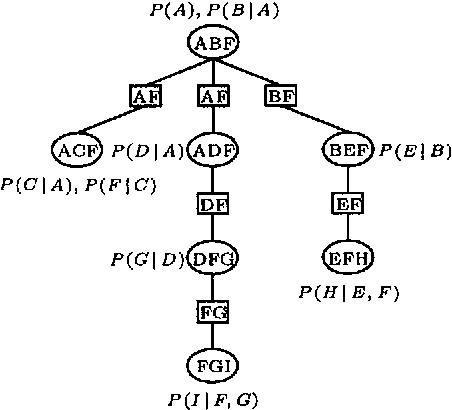
The efficiency of algorithms using secondary structures for probabilistic inference in Bayesian networks can be improved by exploiting independence relations induced by evidence and the direction of the links in the original network. In this paper we present an algorithm that on-line exploits independence relations induced by evidence and the direction of the links in the original network to reduce both time and space costs. Instead of multiplying the conditional probability distributions for the various cliques, we determine on-line which potentials to multiply when a message is to be produced. The performance improvement of the algorithm is emphasized through empirical evaluations involving large real world Bayesian networks, and we compare the method with the HUGIN and Shafer-Shenoy inference algorithms.

Inference in Multiply Sectioned Bayesian Networks with Extended Shafer-Shenoy and Lazy Propagation

As Bayesian networks are applied to larger and more complex problem domains, search for flexible modeling and more efficient inference methods is an ongoing effort. Multiply sectioned Bayesian networks (MSBNs) extend the HUGIN inference for Bayesian networks into a coherent framework for flexible modeling and distributed inference.Lazy propagation extends the Shafer-Shenoy and HUGIN inference methods with reduced space complexity. We apply the Shafer-Shenoy and lazy propagation to inference in MSBNs. The combination of the MSBN framework and lazy propagation provides a better framework for modeling and inference in very large domains. It retains the modeling flexibility of MSBNs and reduces the runtime space complexity, allowing exact inference in much larger domains given the same computational resources.

Welldefined Decision Scenarios

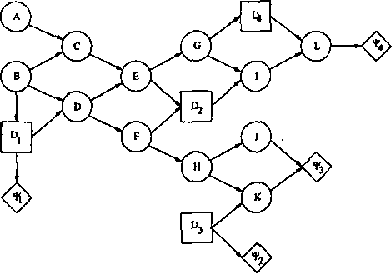
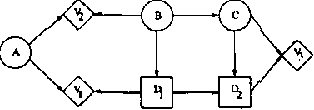
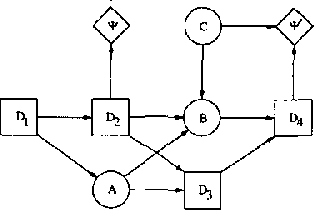
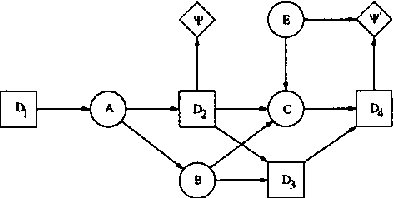
Influence diagrams serve as a powerful tool for modelling symmetric decision problems. When solving an influence diagram we determine a set of strategies for the decisions involved. A strategy for a decision variable is in principle a function over its past. However, some of the past may be irrelevant for the decision, and for computational reasons it is important not to deal with redundant variables in the strategies. We show that current methods (e.g. the "Decision Bayes-ball" algorithm by Shachter UAI98) do not determine the relevant past, and we present a complete algorithm. Actually, this paper takes a more general outset: When formulating a decision scenario as an influence diagram, a linear temporal ordering of the decisions variables is required. This constraint ensures that the decision scenario is welldefined. However, the structure of a decision scenario often yields certain decisions conditionally independent, and it is therefore unnecessary to impose a linear temporal ordering on the decisions. In this paper we deal with partial influence diagrams i.e. influence diagrams with only a partial temporal ordering specified. We present a set of conditions which are necessary and sufficient to ensure that a partial influence diagram is welldefined. These conditions are used as a basis for the construction of an algorithm for determining whether or not a partial influence diagram is welldefined.