From Influence Diagrams to Junction Trees

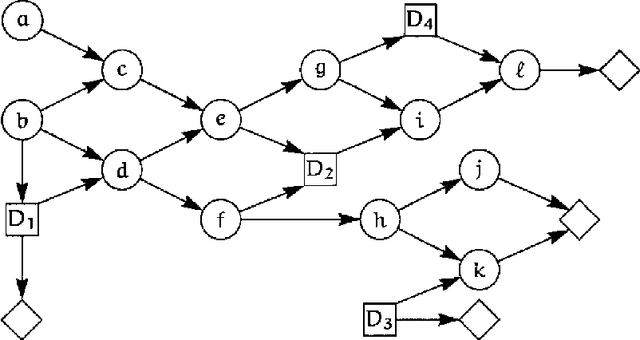
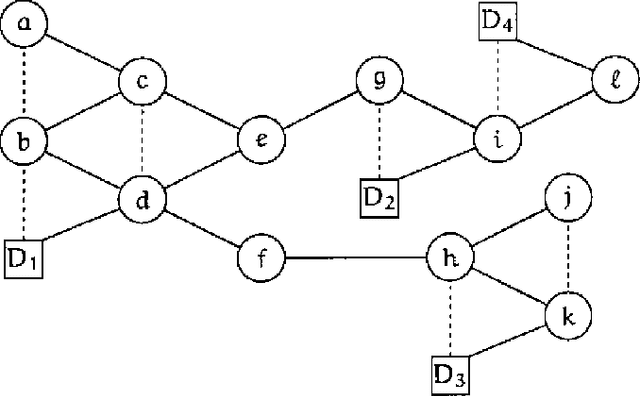
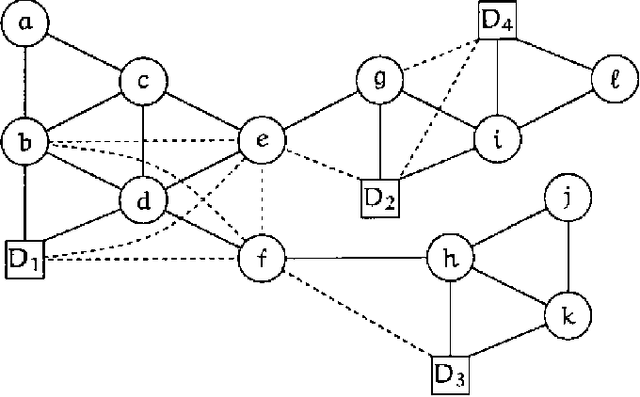
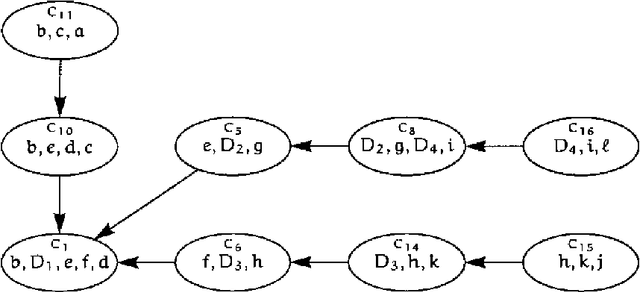
We present an approach to the solution of decision problems formulated as influence diagrams. This approach involves a special triangulation of the underlying graph, the construction of a junction tree with special properties, and a message passing algorithm operating on the junction tree for computation of expected utilities and optimal decision policies.

Myopic Value of Information in Influence Diagrams

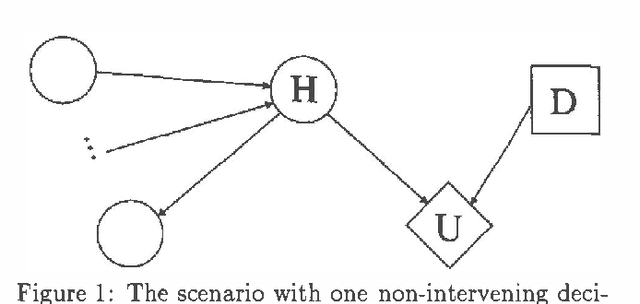
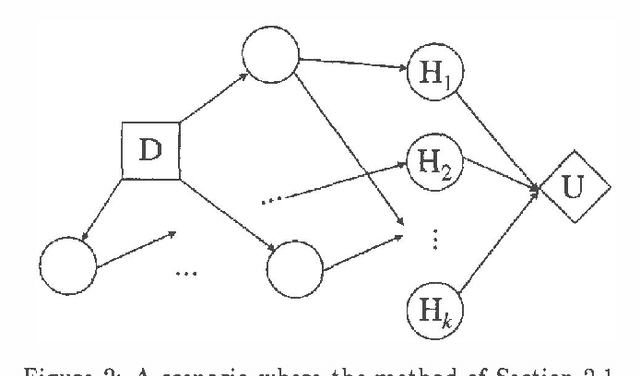
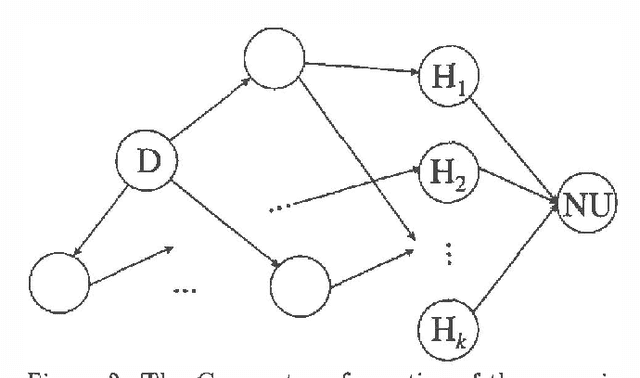
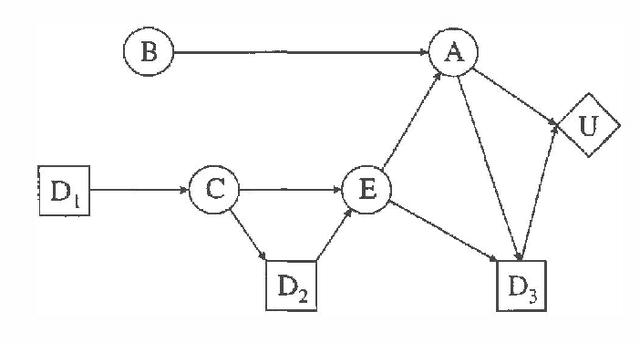
We present a method for calculation of myopic value of information in influence diagrams (Howard & Matheson, 1981) based on the strong junction tree framework (Jensen, Jensen & Dittmer, 1994). The difference in instantiation order in the influence diagrams is reflected in the corresponding junction trees by the order in which the chance nodes are marginalized. This order of marginalization can be changed by table expansion and in effect the same junction tree with expanded tables may be used for calculating the expected utility for scenarios with different instantiation order. We also compare our method to the classic method of modeling different instantiation orders in the same influence diagram.