MM Algorithms to Estimate Parameters in Continuous-time Markov Chains

Continuous-time Markov chains (CTMCs) are popular modeling formalism that constitutes the underlying semantics for real-time probabilistic systems such as queuing networks, stochastic process algebras, and calculi for systems biology. Prism and Storm are popular model checking tools that provide a number of powerful analysis techniques for CTMCs. These tools accept models expressed as the parallel composition of a number of modules interacting with each other. The outcome of the analysis is strongly dependent on the parameter values used in the model which govern the timing and probability of events of the resulting CTMC. However, for some applications, parameter values have to be empirically estimated from partially-observable executions. In this work, we address the problem of estimating parameter values of CTMCs expressed as Prism models from a number of partially-observable executions. We introduce the class parametric CTMCs -- CTMCs where transition rates are polynomial functions over a set of parameters -- as an abstraction of CTMCs covering a large class of Prism models. Then, building on a theory of algorithms known by the initials MM, for minorization-maximization, we present iterative maximum likelihood estimation algorithms for parametric CTMCs covering two learning scenarios: when both state-labels and dwell times are observable, or just state-labels are. We conclude by illustrating the use of our technique in a simple but non-trivial case study: the analysis of the spread of COVID-19 in presence of lockdown countermeasures.

A general framework for defining and optimizing robustness

Robustness of neural networks has recently attracted a great amount of interest. The many investigations in this area lack a precise common foundation of robustness concepts. Therefore, in this paper, we propose a rigorous and flexible framework for defining different types of robustness that also help to explain the interplay between adversarial robustness and generalization. The different robustness objectives directly lead to an adjustable family of loss functions. For two robustness concepts of particular interest we show effective ways to minimize the corresponding loss functions. One loss is designed to strengthen robustness against adversarial off-manifold attacks, and another to improve generalization under the given data distribution. Empirical results show that we can effectively train under different robustness objectives, obtaining higher robustness scores and better generalization, for the two examples respectively, compared to the state-of-the-art data augmentation and regularization techniques.

L*-Based Learning of Markov Decision Processes

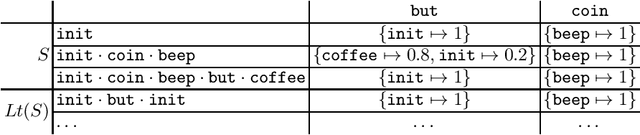
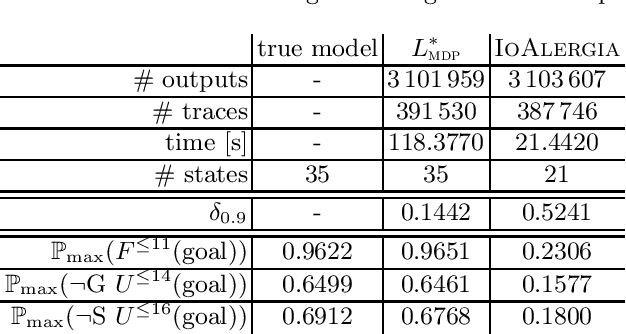
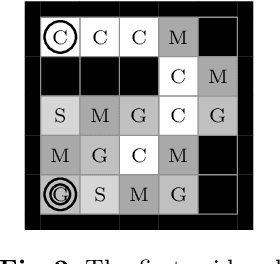
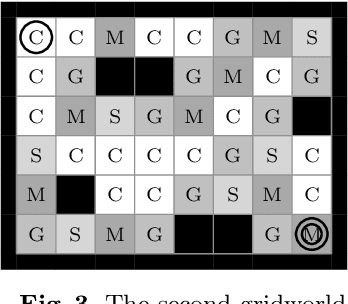
Automata learning techniques automatically generate system models from test observations. These techniques usually fall into two categories: passive and active. Passive learning uses a predetermined data set, e.g., system logs. In contrast, active learning actively queries the system under learning, which is considered more efficient. An influential active learning technique is Angluin's L* algorithm for regular languages which inspired several generalisations from DFAs to other automata-based modelling formalisms. In this work, we study L*-based learning of deterministic Markov decision processes, first assuming an ideal setting with perfect information. Then, we relax this assumption and present a novel learning algorithm that collects information by sampling system traces via testing. Experiments with the implementation of our sampling-based algorithm suggest that it achieves better accuracy than state-of-the-art passive learning techniques with the same amount of test data. Unlike existing learning algorithms with predefined states, our algorithm learns the complete model structure including the states.

Learning Markov Decision Processes for Model Checking

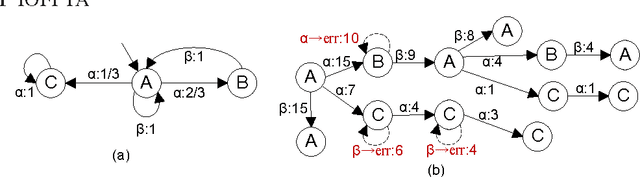
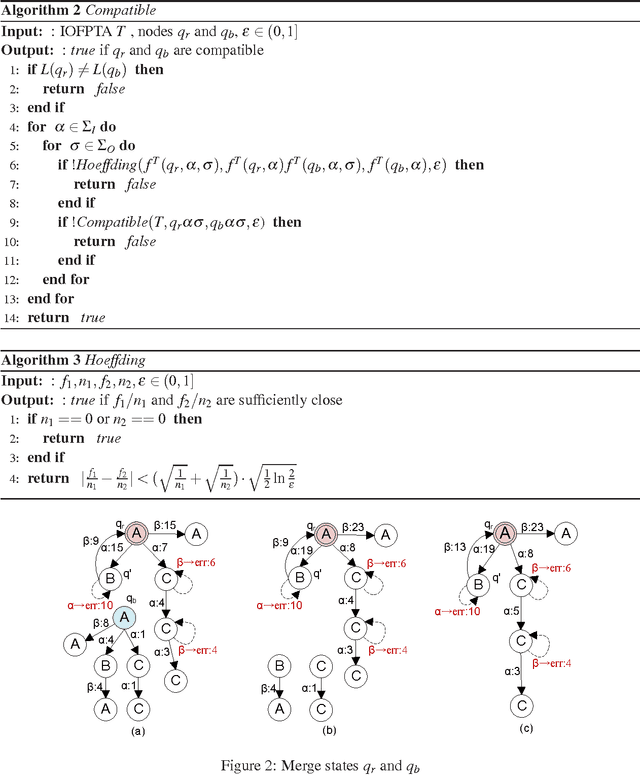
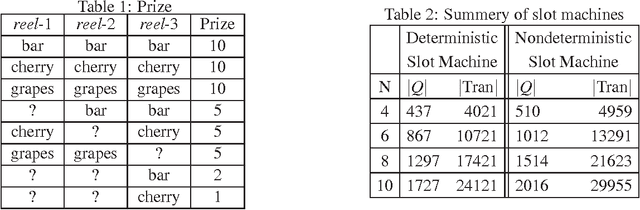
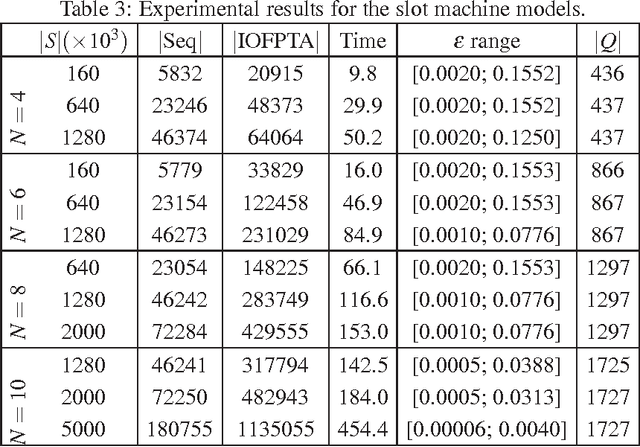
Constructing an accurate system model for formal model verification can be both resource demanding and time-consuming. To alleviate this shortcoming, algorithms have been proposed for automatically learning system models based on observed system behaviors. In this paper we extend the algorithm on learning probabilistic automata to reactive systems, where the observed system behavior is in the form of alternating sequences of inputs and outputs. We propose an algorithm for automatically learning a deterministic labeled Markov decision process model from the observed behavior of a reactive system. The proposed learning algorithm is adapted from algorithms for learning deterministic probabilistic finite automata, and extended to include both probabilistic and nondeterministic transitions. The algorithm is empirically analyzed and evaluated by learning system models of slot machines. The evaluation is performed by analyzing the probabilistic linear temporal logic properties of the system as well as by analyzing the schedulers, in particular the optimal schedulers, induced by the learned models.