Self-Supervised Conditional Distribution Learning on Graphs

Graph contrastive learning (GCL) has shown promising performance in semisupervised graph classification. However, existing studies still encounter significant challenges in GCL. First, successive layers in graph neural network (GNN) tend to produce more similar node embeddings, while GCL aims to increase the dissimilarity between negative pairs of node embeddings. This inevitably results in a conflict between the message-passing mechanism of GNNs and the contrastive learning of negative pairs via intraviews. Second, leveraging the diversity and quantity of data provided by graph-structured data augmentations while preserving intrinsic semantic information is challenging. In this paper, we propose a self-supervised conditional distribution learning (SSCDL) method designed to learn graph representations from graph-structured data for semisupervised graph classification. Specifically, we present an end-to-end graph representation learning model to align the conditional distributions of weakly and strongly augmented features over the original features. This alignment effectively reduces the risk of disrupting intrinsic semantic information through graph-structured data augmentation. To avoid conflict between the message-passing mechanism and contrastive learning of negative pairs, positive pairs of node representations are retained for measuring the similarity between the original features and the corresponding weakly augmented features. Extensive experiments with several benchmark graph datasets demonstrate the effectiveness of the proposed SSCDL method.

Hierarchical Sparse Representation Clustering for High-Dimensional Data Streams

Data stream clustering reveals patterns within continuously arriving, potentially unbounded data sequences. Numerous data stream algorithms have been proposed to cluster data streams. The existing data stream clustering algorithms still face significant challenges when addressing high-dimensional data streams. First, it is intractable to measure the similarities among high-dimensional data objects via Euclidean distances when constructing and merging microclusters. Second, these algorithms are highly sensitive to the noise contained in high-dimensional data streams. In this paper, we propose a hierarchical sparse representation clustering (HSRC) method for clustering high-dimensional data streams. HSRC first employs an $l_1$-minimization technique to learn an affinity matrix for data objects in individual landmark windows with fixed sizes, where the number of neighboring data objects is automatically selected. This approach ensures that highly correlated data samples within clusters are grouped together. Then, HSRC applies a spectral clustering technique to the affinity matrix to generate microclusters. These microclusters are subsequently merged into macroclusters based on their sparse similarity degrees (SSDs). Additionally, HSRC introduces sparsity residual values (SRVs) to adaptively select representative data objects from the current landmark window. These representatives serve as dictionary samples for the next landmark window. Finally, HSRC refines each macrocluster through fine-tuning. In particular, HSRC enables the detection of outliers in high-dimensional data streams via the associated SRVs. The experimental results obtained on several benchmark datasets demonstrate the effectiveness and robustness of HSRC.

Consistency Enhancement-Based Deep Multiview Clustering via Contrastive Learning

Multiview clustering (MVC) segregates data samples into meaningful clusters by synthesizing information across multiple views. Moreover, deep learning-based methods have demonstrated their strong feature learning capabilities in MVC scenarios. However, effectively generalizing feature representations while maintaining consistency is still an intractable problem. In addition, most existing deep clustering methods based on contrastive learning overlook the consistency of the clustering representations during the clustering process. In this paper, we show how the above problems can be overcome and propose a consistent enhancement-based deep MVC method via contrastive learning (CCEC). Specifically, semantic connection blocks are incorporated into a feature representation to preserve the consistent information among multiple views. Furthermore, the representation process for clustering is enhanced through spectral clustering, and the consistency across multiple views is improved. Experiments conducted on five datasets demonstrate the effectiveness and superiority of our method in comparison with the state-of-the-art (SOTA) methods. The code for this method can be accessed at https://anonymous.4open.science/r/CCEC-E84E/.

Cross-View Graph Consistency Learning for Invariant Graph Representations

Graph representation learning is fundamental for analyzing graph-structured data. Exploring invariant graph representations remains a challenge for most existing graph representation learning methods. In this paper, we propose a cross-view graph consistency learning (CGCL) method that learns invariant graph representations for link prediction. First, two complementary augmented views are derived from an incomplete graph structure through a bidirectional graph structure augmentation scheme. This augmentation scheme mitigates the potential information loss that is commonly associated with various data augmentation techniques involving raw graph data, such as edge perturbation, node removal, and attribute masking. Second, we propose a CGCL model that can learn invariant graph representations. A cross-view training scheme is proposed to train the proposed CGCL model. This scheme attempts to maximize the consistency information between one augmented view and the graph structure reconstructed from the other augmented view. Furthermore, we offer a comprehensive theoretical CGCL analysis. This paper empirically and experimentally demonstrates the effectiveness of the proposed CGCL method, achieving competitive results on graph datasets in comparisons with several state-of-the-art algorithms.

Deep Multiview Clustering by Contrasting Cluster Assignments

Multiview clustering (MVC) aims to reveal the underlying structure of multiview data by categorizing data samples into clusters. Deep learning-based methods exhibit strong feature learning capabilities on large-scale datasets. For most existing deep MVC methods, exploring the invariant representations of multiple views is still an intractable problem. In this paper, we propose a cross-view contrastive learning (CVCL) method that learns view-invariant representations and produces clustering results by contrasting the cluster assignments among multiple views. Specifically, we first employ deep autoencoders to extract view-dependent features in the pretraining stage. Then, a cluster-level CVCL strategy is presented to explore consistent semantic label information among the multiple views in the fine-tuning stage. Thus, the proposed CVCL method is able to produce more discriminative cluster assignments by virtue of this learning strategy. Moreover, we provide a theoretical analysis of soft cluster assignment alignment. Extensive experimental results obtained on several datasets demonstrate that the proposed CVCL method outperforms several state-of-the-art approaches.

Subspace clustering using a symmetric low-rank representation

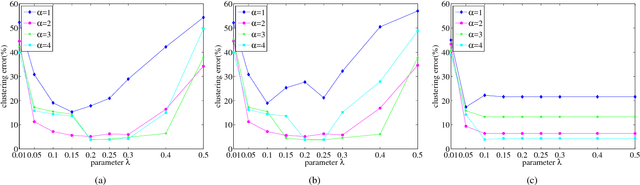
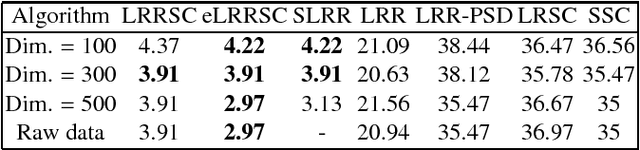
In this paper, we propose a low-rank representation with symmetric constraint (LRRSC) method for robust subspace clustering. Given a collection of data points approximately drawn from multiple subspaces, the proposed technique can simultaneously recover the dimension and members of each subspace. LRRSC extends the original low-rank representation algorithm by integrating a symmetric constraint into the low-rankness property of high-dimensional data representation. The symmetric low-rank representation, which preserves the subspace structures of high-dimensional data, guarantees weight consistency for each pair of data points so that highly correlated data points of subspaces are represented together. Moreover, it can be efficiently calculated by solving a convex optimization problem. We provide a rigorous proof for minimizing the nuclear-norm regularized least square problem with a symmetric constraint. The affinity matrix for spectral clustering can be obtained by further exploiting the angular information of the principal directions of the symmetric low-rank representation. This is a critical step towards evaluating the memberships between data points. Experimental results on benchmark databases demonstrate the effectiveness and robustness of LRRSC compared with several state-of-the-art subspace clustering algorithms.

Symmetric low-rank representation for subspace clustering

We propose a symmetric low-rank representation (SLRR) method for subspace clustering, which assumes that a data set is approximately drawn from the union of multiple subspaces. The proposed technique can reveal the membership of multiple subspaces through the self-expressiveness property of the data. In particular, the SLRR method considers a collaborative representation combined with low-rank matrix recovery techniques as a low-rank representation to learn a symmetric low-rank representation, which preserves the subspace structures of high-dimensional data. In contrast to performing iterative singular value decomposition in some existing low-rank representation based algorithms, the symmetric low-rank representation in the SLRR method can be calculated as a closed form solution by solving the symmetric low-rank optimization problem. By making use of the angular information of the principal directions of the symmetric low-rank representation, an affinity graph matrix is constructed for spectral clustering. Extensive experimental results show that it outperforms state-of-the-art subspace clustering algorithms.

Learning Markov Decision Processes for Model Checking

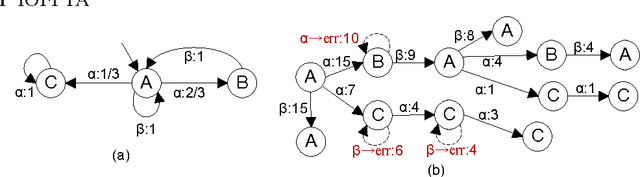
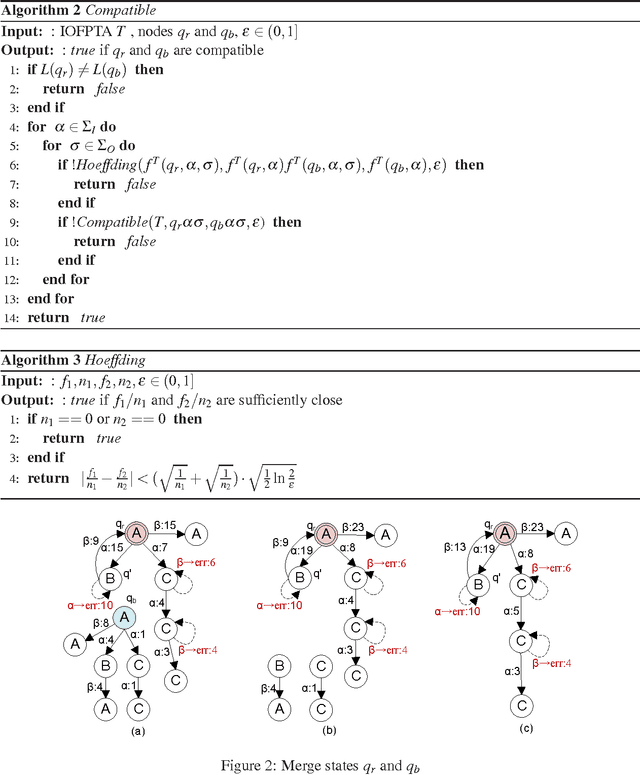
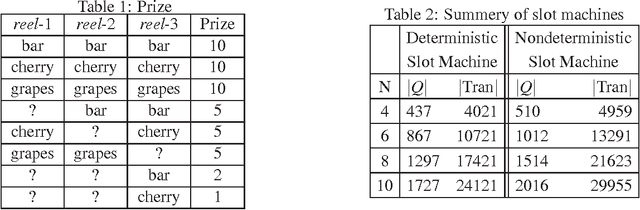
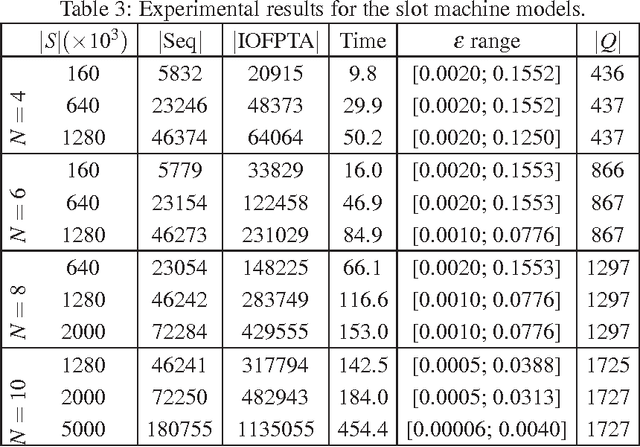
Constructing an accurate system model for formal model verification can be both resource demanding and time-consuming. To alleviate this shortcoming, algorithms have been proposed for automatically learning system models based on observed system behaviors. In this paper we extend the algorithm on learning probabilistic automata to reactive systems, where the observed system behavior is in the form of alternating sequences of inputs and outputs. We propose an algorithm for automatically learning a deterministic labeled Markov decision process model from the observed behavior of a reactive system. The proposed learning algorithm is adapted from algorithms for learning deterministic probabilistic finite automata, and extended to include both probabilistic and nondeterministic transitions. The algorithm is empirically analyzed and evaluated by learning system models of slot machines. The evaluation is performed by analyzing the probabilistic linear temporal logic properties of the system as well as by analyzing the schedulers, in particular the optimal schedulers, induced by the learned models.