Subspace clustering using a symmetric low-rank representation
Paper and Code
May 13, 2017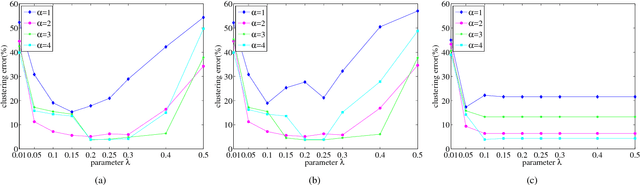
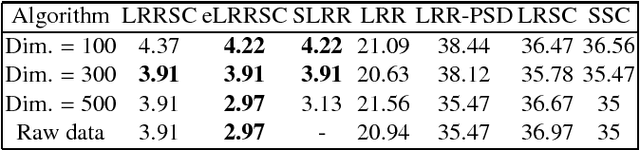


In this paper, we propose a low-rank representation with symmetric constraint (LRRSC) method for robust subspace clustering. Given a collection of data points approximately drawn from multiple subspaces, the proposed technique can simultaneously recover the dimension and members of each subspace. LRRSC extends the original low-rank representation algorithm by integrating a symmetric constraint into the low-rankness property of high-dimensional data representation. The symmetric low-rank representation, which preserves the subspace structures of high-dimensional data, guarantees weight consistency for each pair of data points so that highly correlated data points of subspaces are represented together. Moreover, it can be efficiently calculated by solving a convex optimization problem. We provide a rigorous proof for minimizing the nuclear-norm regularized least square problem with a symmetric constraint. The affinity matrix for spectral clustering can be obtained by further exploiting the angular information of the principal directions of the symmetric low-rank representation. This is a critical step towards evaluating the memberships between data points. Experimental results on benchmark databases demonstrate the effectiveness and robustness of LRRSC compared with several state-of-the-art subspace clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge