Yongsheng Sang
Generating Chinese Poetry from Images via Concrete and Abstract Information
Mar 24, 2020
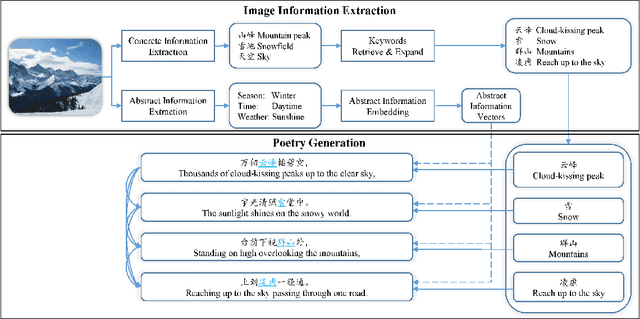


Abstract:In recent years, the automatic generation of classical Chinese poetry has made great progress. Besides focusing on improving the quality of the generated poetry, there is a new topic about generating poetry from an image. However, the existing methods for this topic still have the problem of topic drift and semantic inconsistency, and the image-poem pairs dataset is hard to be built when training these models. In this paper, we extract and integrate the Concrete and Abstract information from images to address those issues. We proposed an infilling-based Chinese poetry generation model which can infill the Concrete keywords into each line of poems in an explicit way, and an abstract information embedding to integrate the Abstract information into generated poems. In addition, we use non-parallel data during training and construct separate image datasets and poem datasets to train the different components in our framework. Both automatic and human evaluation results show that our approach can generate poems which have better consistency with images without losing the quality.
Subspace clustering using a symmetric low-rank representation
May 13, 2017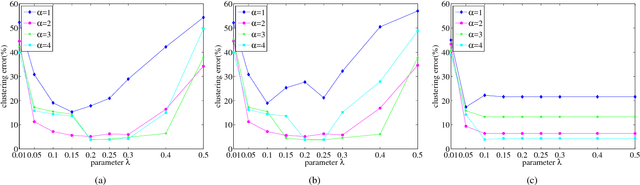
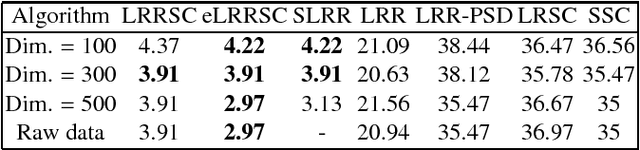


Abstract:In this paper, we propose a low-rank representation with symmetric constraint (LRRSC) method for robust subspace clustering. Given a collection of data points approximately drawn from multiple subspaces, the proposed technique can simultaneously recover the dimension and members of each subspace. LRRSC extends the original low-rank representation algorithm by integrating a symmetric constraint into the low-rankness property of high-dimensional data representation. The symmetric low-rank representation, which preserves the subspace structures of high-dimensional data, guarantees weight consistency for each pair of data points so that highly correlated data points of subspaces are represented together. Moreover, it can be efficiently calculated by solving a convex optimization problem. We provide a rigorous proof for minimizing the nuclear-norm regularized least square problem with a symmetric constraint. The affinity matrix for spectral clustering can be obtained by further exploiting the angular information of the principal directions of the symmetric low-rank representation. This is a critical step towards evaluating the memberships between data points. Experimental results on benchmark databases demonstrate the effectiveness and robustness of LRRSC compared with several state-of-the-art subspace clustering algorithms.
Symmetric low-rank representation for subspace clustering
May 21, 2015



Abstract:We propose a symmetric low-rank representation (SLRR) method for subspace clustering, which assumes that a data set is approximately drawn from the union of multiple subspaces. The proposed technique can reveal the membership of multiple subspaces through the self-expressiveness property of the data. In particular, the SLRR method considers a collaborative representation combined with low-rank matrix recovery techniques as a low-rank representation to learn a symmetric low-rank representation, which preserves the subspace structures of high-dimensional data. In contrast to performing iterative singular value decomposition in some existing low-rank representation based algorithms, the symmetric low-rank representation in the SLRR method can be calculated as a closed form solution by solving the symmetric low-rank optimization problem. By making use of the angular information of the principal directions of the symmetric low-rank representation, an affinity graph matrix is constructed for spectral clustering. Extensive experimental results show that it outperforms state-of-the-art subspace clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge