Latent Instrumental Variables as Priors in Causal Inference based on Independence of Cause and Mechanism

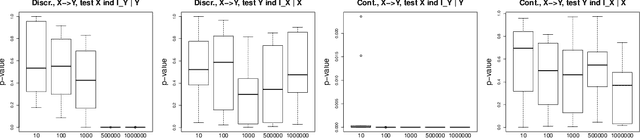
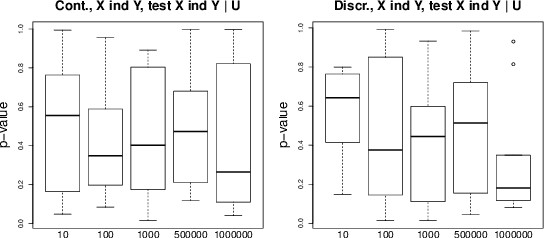
Causal inference methods based on conditional independence construct Markov equivalent graphs, and cannot be applied to bivariate cases. The approaches based on independence of cause and mechanism state, on the contrary, that causal discovery can be inferred for two observations. In our contribution, we challenge to reconcile these two research directions. We study the role of latent variables such as latent instrumental variables and hidden common causes in the causal graphical structures. We show that the methods based on the independence of cause and mechanism, indirectly contain traces of the existence of the hidden instrumental variables. We derive a novel algorithm to infer causal relationships between two variables, and we validate the proposed method on simulated data and on a benchmark of cause-effect pairs. We illustrate by our experiments that the proposed approach is simple and extremely competitive in terms of empirical accuracy compared to the state-of-the-art methods.

Using ROBDDs for Inference in Bayesian Networks with Troubleshooting as an Example

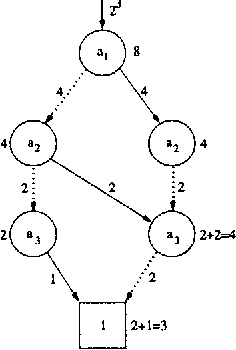
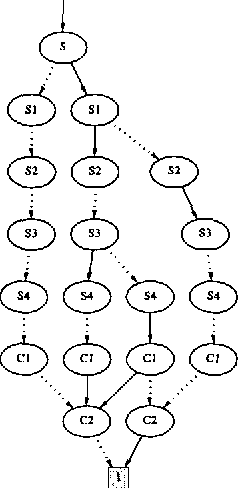
When using Bayesian networks for modelling the behavior of man-made machinery, it usually happens that a large part of the model is deterministic. For such Bayesian networks deterministic part of the model can be represented as a Boolean function, and a central part of belief updating reduces to the task of calculating the number of satisfying configurations in a Boolean function. In this paper we explore how advances in the calculation of Boolean functions can be adopted for belief updating, in particular within the context of troubleshooting. We present experimental results indicating a substantial speed-up compared to traditional junction tree propagation.

Chi-square Tests Driven Method for Learning the Structure of Factored MDPs

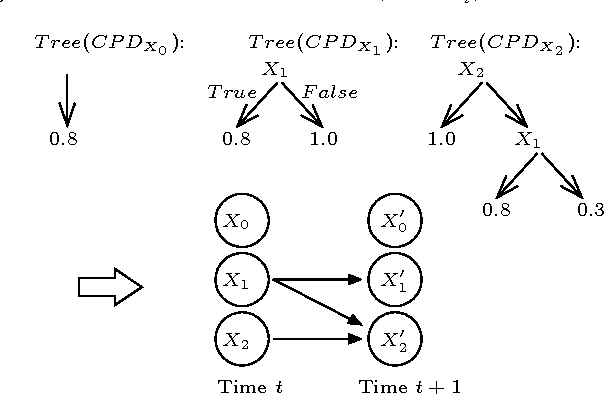
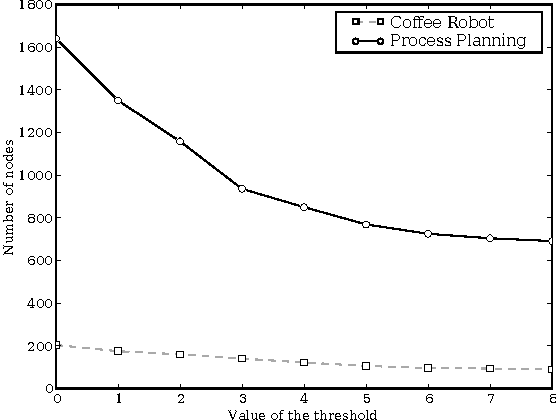
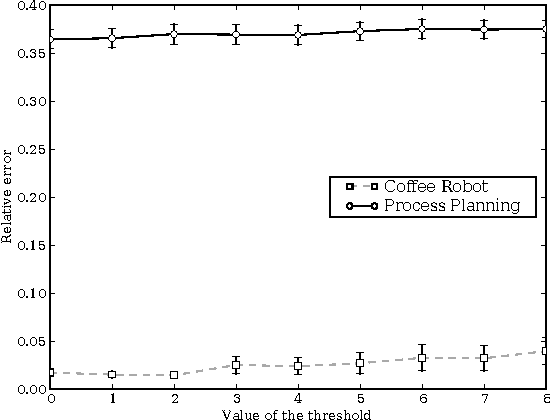
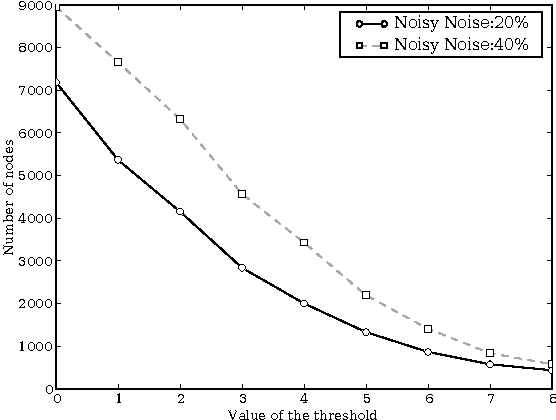
SDYNA is a general framework designed to address large stochastic reinforcement learning problems. Unlike previous model based methods in FMDPs, it incrementally learns the structure and the parameters of a RL problem using supervised learning techniques. Then, it integrates decision-theoric planning algorithms based on FMDPs to compute its policy. SPITI is an instanciation of SDYNA that exploits ITI, an incremental decision tree algorithm, to learn the reward function and the Dynamic Bayesian Networks with local structures representing the transition function of the problem. These representations are used by an incremental version of the Structured Value Iteration algorithm. In order to learn the structure, SPITI uses Chi-Square tests to detect the independence between two probability distributions. Thus, we study the relation between the threshold used in the Chi-Square test, the size of the model built and the relative error of the value function of the induced policy with respect to the optimal value. We show that, on stochastic problems, one can tune the threshold so as to generate both a compact model and an efficient policy. Then, we show that SPITI, while keeping its model compact, uses the generalization property of its learning method to perform better than a stochastic classical tabular algorithm in large RL problem with an unknown structure. We also introduce a new measure based on Chi-Square to qualify the accuracy of the model learned by SPITI. We qualitatively show that the generalization property in SPITI within the FMDP framework may prevent an exponential growth of the time required to learn the structure of large stochastic RL problems.