Latent Instrumental Variables as Priors in Causal Inference based on Independence of Cause and Mechanism
Paper and Code
Jul 17, 2020
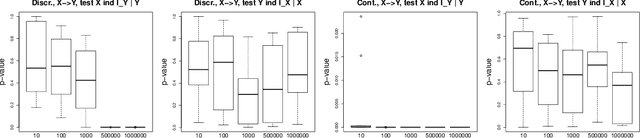

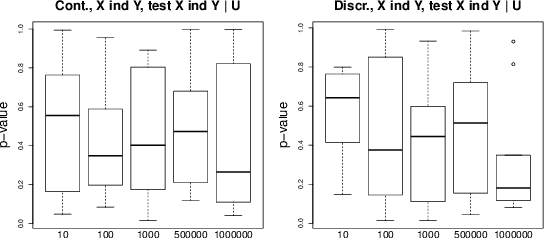
Causal inference methods based on conditional independence construct Markov equivalent graphs, and cannot be applied to bivariate cases. The approaches based on independence of cause and mechanism state, on the contrary, that causal discovery can be inferred for two observations. In our contribution, we challenge to reconcile these two research directions. We study the role of latent variables such as latent instrumental variables and hidden common causes in the causal graphical structures. We show that the methods based on the independence of cause and mechanism, indirectly contain traces of the existence of the hidden instrumental variables. We derive a novel algorithm to infer causal relationships between two variables, and we validate the proposed method on simulated data and on a benchmark of cause-effect pairs. We illustrate by our experiments that the proposed approach is simple and extremely competitive in terms of empirical accuracy compared to the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge