Thomas Degris
Step-size Optimization for Continual Learning
Jan 30, 2024Abstract:In continual learning, a learner has to keep learning from the data over its whole life time. A key issue is to decide what knowledge to keep and what knowledge to let go. In a neural network, this can be implemented by using a step-size vector to scale how much gradient samples change network weights. Common algorithms, like RMSProp and Adam, use heuristics, specifically normalization, to adapt this step-size vector. In this paper, we show that those heuristics ignore the effect of their adaptation on the overall objective function, for example by moving the step-size vector away from better step-size vectors. On the other hand, stochastic meta-gradient descent algorithms, like IDBD (Sutton, 1992), explicitly optimize the step-size vector with respect to the overall objective function. On simple problems, we show that IDBD is able to consistently improve step-size vectors, where RMSProp and Adam do not. We explain the differences between the two approaches and their respective limitations. We conclude by suggesting that combining both approaches could be a promising future direction to improve the performance of neural networks in continual learning.
Meta-descent for Online, Continual Prediction
Jul 17, 2019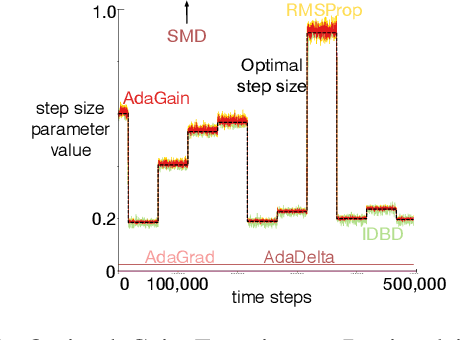
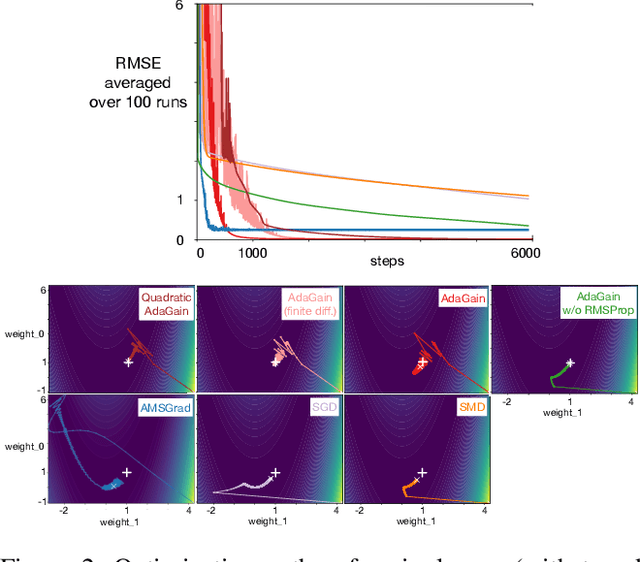
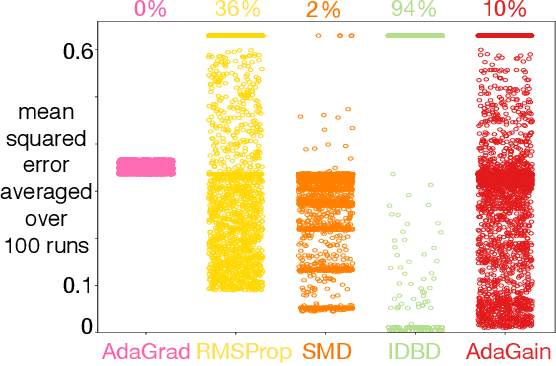
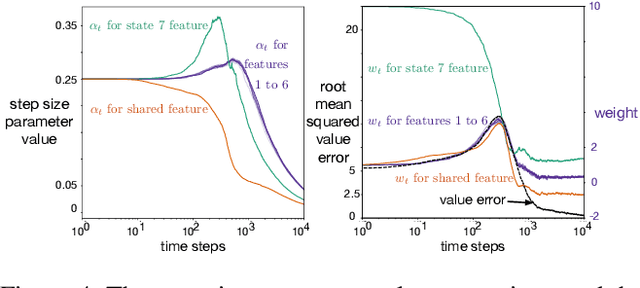
Abstract:This paper investigates different vector step-size adaptation approaches for non-stationary online, continual prediction problems. Vanilla stochastic gradient descent can be considerably improved by scaling the update with a vector of appropriately chosen step-sizes. Many methods, including AdaGrad, RMSProp, and AMSGrad, keep statistics about the learning process to approximate a second order update---a vector approximation of the inverse Hessian. Another family of approaches use meta-gradient descent to adapt the step-size parameters to minimize prediction error. These meta-descent strategies are promising for non-stationary problems, but have not been as extensively explored as quasi-second order methods. We first derive a general, incremental meta-descent algorithm, called AdaGain, designed to be applicable to a much broader range of algorithms, including those with semi-gradient updates or even those with accelerations, such as RMSProp. We provide an empirical comparison of methods from both families. We conclude that methods from both families can perform well, but in non-stationary prediction problems the meta-descent methods exhibit advantages. Our method is particularly robust across several prediction problems, and is competitive with the state-of-the-art method on a large-scale, time-series prediction problem on real data from a mobile robot.
Adapting Behaviour via Intrinsic Reward: A Survey and Empirical Study
Jun 19, 2019



Abstract:Learning about many things can provide numerous benefits to a reinforcement learning system. For example, learning many auxiliary value functions, in addition to optimizing the environmental reward, appears to improve both exploration and representation learning. The question we tackle in this paper is how to sculpt the stream of experience---how to adapt the system's behaviour---to optimize the learning of a collection of value functions. A simple answer is to compute an intrinsic reward based on the statistics of each auxiliary learner, and use reinforcement learning to maximize that intrinsic reward. Unfortunately, implementing this simple idea has proven difficult, and thus has been the focus of decades of study. It remains unclear which of the many possible measures of learning would work well in a parallel learning setting where environmental reward is extremely sparse or absent. In this paper, we investigate and compare different intrinsic reward mechanisms in a new bandit-like parallel-learning testbed. We discuss the interaction between reward and prediction learners and highlight the importance of introspective prediction learners: those that increase their rate of learning when progress is possible, and decrease when it is not. We provide a comprehensive empirical comparison of 15 different rewards, including well-known ideas from reinforcement learning and active learning. Our results highlight a simple but seemingly powerful principle: intrinsic rewards based on the amount of learning can generate useful behaviour, if each individual learner is introspective.
The Predictron: End-To-End Learning and Planning
Jul 20, 2017



Abstract:One of the key challenges of artificial intelligence is to learn models that are effective in the context of planning. In this document we introduce the predictron architecture. The predictron consists of a fully abstract model, represented by a Markov reward process, that can be rolled forward multiple "imagined" planning steps. Each forward pass of the predictron accumulates internal rewards and values over multiple planning depths. The predictron is trained end-to-end so as to make these accumulated values accurately approximate the true value function. We applied the predictron to procedurally generated random mazes and a simulator for the game of pool. The predictron yielded significantly more accurate predictions than conventional deep neural network architectures.
Deep Reinforcement Learning in Large Discrete Action Spaces
Apr 04, 2016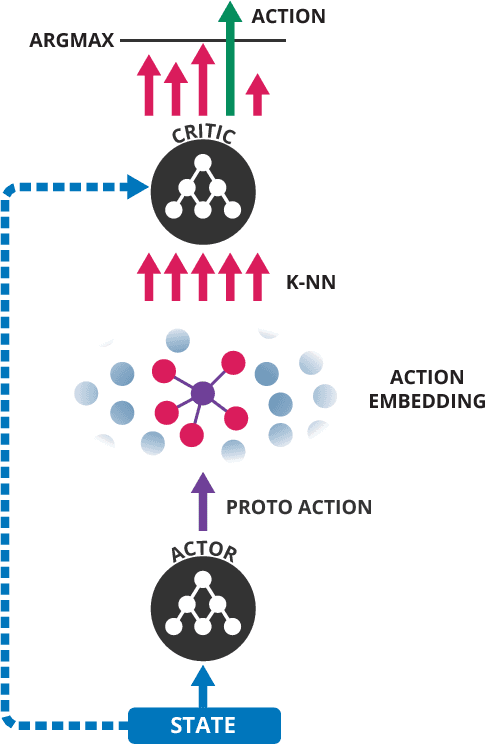

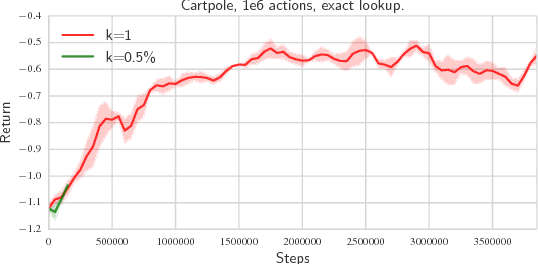
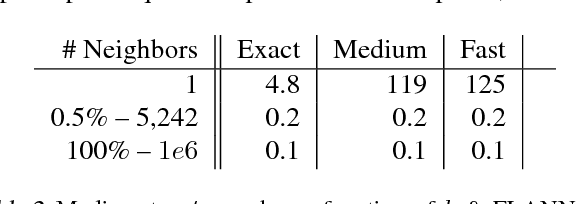
Abstract:Being able to reason in an environment with a large number of discrete actions is essential to bringing reinforcement learning to a larger class of problems. Recommender systems, industrial plants and language models are only some of the many real-world tasks involving large numbers of discrete actions for which current methods are difficult or even often impossible to apply. An ability to generalize over the set of actions as well as sub-linear complexity relative to the size of the set are both necessary to handle such tasks. Current approaches are not able to provide both of these, which motivates the work in this paper. Our proposed approach leverages prior information about the actions to embed them in a continuous space upon which it can generalize. Additionally, approximate nearest-neighbor methods allow for logarithmic-time lookup complexity relative to the number of actions, which is necessary for time-wise tractable training. This combined approach allows reinforcement learning methods to be applied to large-scale learning problems previously intractable with current methods. We demonstrate our algorithm's abilities on a series of tasks having up to one million actions.
Off-Policy Actor-Critic
Jun 20, 2013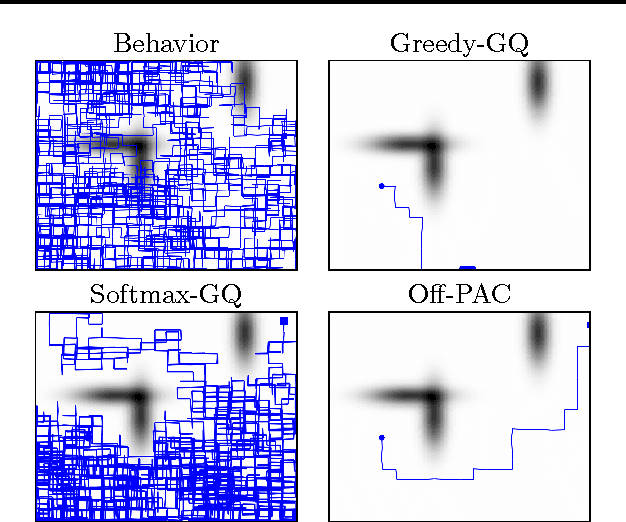
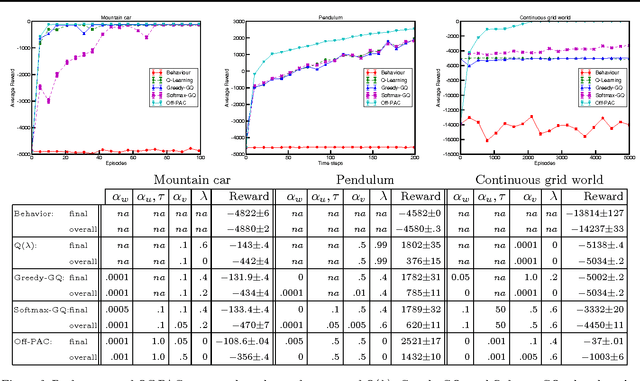
Abstract:This paper presents the first actor-critic algorithm for off-policy reinforcement learning. Our algorithm is online and incremental, and its per-time-step complexity scales linearly with the number of learned weights. Previous work on actor-critic algorithms is limited to the on-policy setting and does not take advantage of the recent advances in off-policy gradient temporal-difference learning. Off-policy techniques, such as Greedy-GQ, enable a target policy to be learned while following and obtaining data from another (behavior) policy. For many problems, however, actor-critic methods are more practical than action value methods (like Greedy-GQ) because they explicitly represent the policy; consequently, the policy can be stochastic and utilize a large action space. In this paper, we illustrate how to practically combine the generality and learning potential of off-policy learning with the flexibility in action selection given by actor-critic methods. We derive an incremental, linear time and space complexity algorithm that includes eligibility traces, prove convergence under assumptions similar to previous off-policy algorithms, and empirically show better or comparable performance to existing algorithms on standard reinforcement-learning benchmark problems.
Chi-square Tests Driven Method for Learning the Structure of Factored MDPs
Jun 27, 2012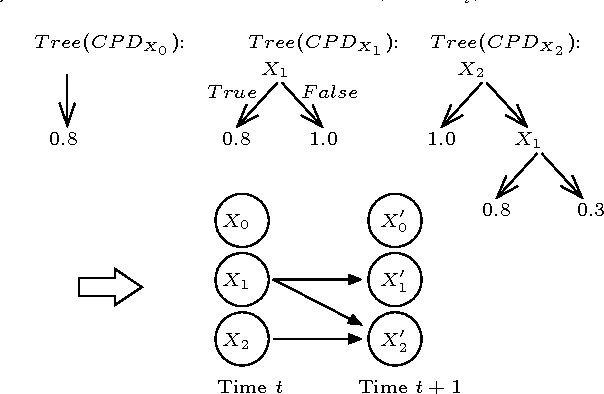
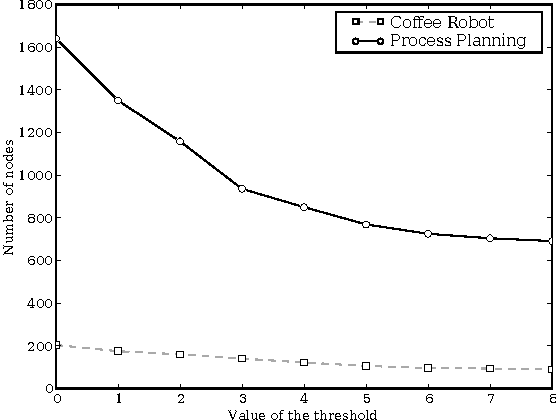
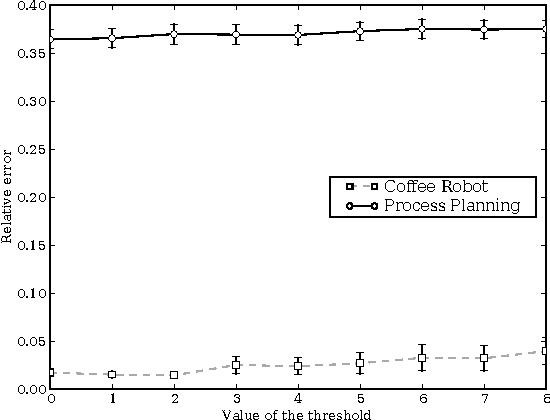
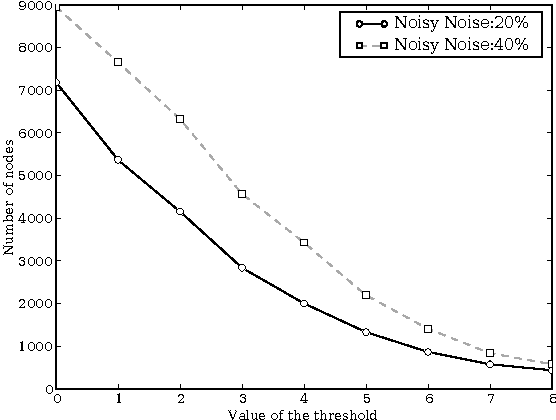
Abstract:SDYNA is a general framework designed to address large stochastic reinforcement learning problems. Unlike previous model based methods in FMDPs, it incrementally learns the structure and the parameters of a RL problem using supervised learning techniques. Then, it integrates decision-theoric planning algorithms based on FMDPs to compute its policy. SPITI is an instanciation of SDYNA that exploits ITI, an incremental decision tree algorithm, to learn the reward function and the Dynamic Bayesian Networks with local structures representing the transition function of the problem. These representations are used by an incremental version of the Structured Value Iteration algorithm. In order to learn the structure, SPITI uses Chi-Square tests to detect the independence between two probability distributions. Thus, we study the relation between the threshold used in the Chi-Square test, the size of the model built and the relative error of the value function of the induced policy with respect to the optimal value. We show that, on stochastic problems, one can tune the threshold so as to generate both a compact model and an efficient policy. Then, we show that SPITI, while keeping its model compact, uses the generalization property of its learning method to perform better than a stochastic classical tabular algorithm in large RL problem with an unknown structure. We also introduce a new measure based on Chi-Square to qualify the accuracy of the model learned by SPITI. We qualitatively show that the generalization property in SPITI within the FMDP framework may prevent an exponential growth of the time required to learn the structure of large stochastic RL problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge