Asynchronous Stochastic Approximation and Average-Reward Reinforcement Learning

This paper studies asynchronous stochastic approximation (SA) algorithms and their application to reinforcement learning in semi-Markov decision processes (SMDPs) with an average-reward criterion. We first extend Borkar and Meyn's stability proof method to accommodate more general noise conditions, leading to broader convergence guarantees for asynchronous SA algorithms. Leveraging these results, we establish the convergence of an asynchronous SA analogue of Schweitzer's classical relative value iteration algorithm, RVI Q-learning, for finite-space, weakly communicating SMDPs. Furthermore, to fully utilize the SA results in this application, we introduce new monotonicity conditions for estimating the optimal reward rate in RVI Q-learning. These conditions substantially expand the previously considered algorithmic framework, and we address them with novel proof arguments in the stability and convergence analysis of RVI Q-learning.

On Convergence of Average-Reward Q-Learning in Weakly Communicating Markov Decision Processes

This paper analyzes reinforcement learning (RL) algorithms for Markov decision processes (MDPs) under the average-reward criterion. We focus on Q-learning algorithms based on relative value iteration (RVI), which are model-free stochastic analogues of the classical RVI method for average-reward MDPs. These algorithms have low per-iteration complexity, making them well-suited for large state space problems. We extend the almost-sure convergence analysis of RVI Q-learning algorithms developed by Abounadi, Bertsekas, and Borkar (2001) from unichain to weakly communicating MDPs. This extension is important both practically and theoretically: weakly communicating MDPs cover a much broader range of applications compared to unichain MDPs, and their optimality equations have a richer solution structure (with multiple degrees of freedom), introducing additional complexity in proving algorithmic convergence. We also characterize the sets to which RVI Q-learning algorithms converge, showing that they are compact, connected, potentially nonconvex, and comprised of solutions to the average-reward optimality equation, with exactly one less degree of freedom than the general solution set of this equation. Furthermore, we extend our analysis to two RVI-based hierarchical average-reward RL algorithms using the options framework, proving their almost-sure convergence and characterizing their sets of convergence under the assumption that the underlying semi-Markov decision process is weakly communicating.

An Idiosyncrasy of Time-discretization in Reinforcement Learning

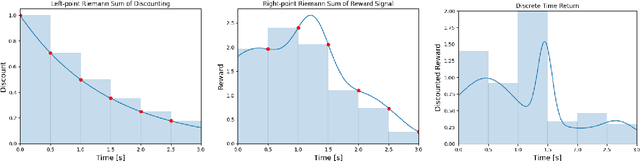
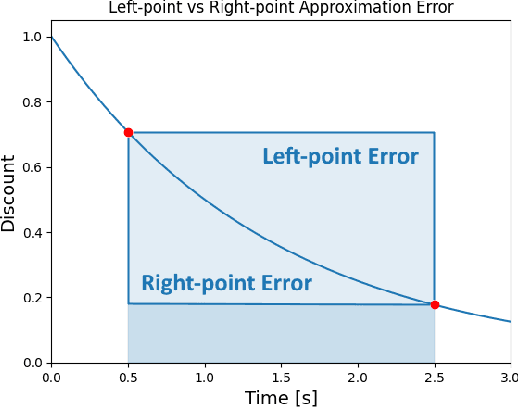
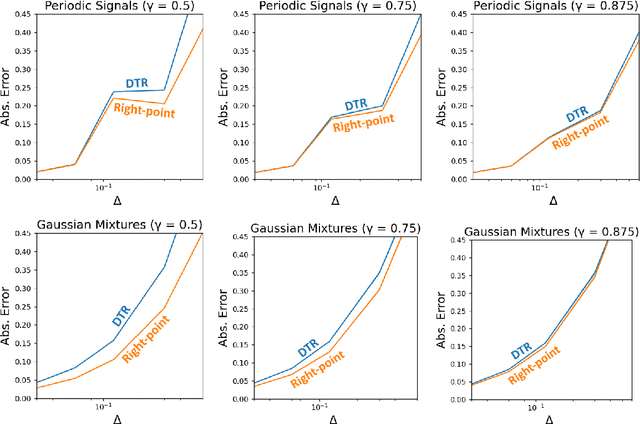
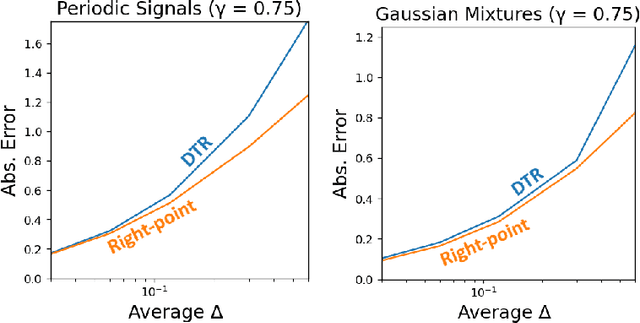
Many reinforcement learning algorithms are built on an assumption that an agent interacts with an environment over fixed-duration, discrete time steps. However, physical systems are continuous in time, requiring a choice of time-discretization granularity when digitally controlling them. Furthermore, such systems do not wait for decisions to be made before advancing the environment state, necessitating the study of how the choice of discretization may affect a reinforcement learning algorithm. In this work, we consider the relationship between the definitions of the continuous-time and discrete-time returns. Specifically, we acknowledge an idiosyncrasy with naively applying a discrete-time algorithm to a discretized continuous-time environment, and note how a simple modification can better align the return definitions. This observation is of practical consideration when dealing with environments where time-discretization granularity is a choice, or situations where such granularity is inherently stochastic.

Reward Centering

We show that discounted methods for solving continuing reinforcement learning problems can perform significantly better if they center their rewards by subtracting out the rewards' empirical average. The improvement is substantial at commonly used discount factors and increases further as the discount factor approaches one. In addition, we show that if a problem's rewards are shifted by a constant, then standard methods perform much worse, whereas methods with reward centering are unaffected. Estimating the average reward is straightforward in the on-policy setting; we propose a slightly more sophisticated method for the off-policy setting. Reward centering is a general idea, so we expect almost every reinforcement-learning algorithm to benefit by the addition of reward centering.

A Note on Stability in Asynchronous Stochastic Approximation without Communication Delays

In this paper, we study asynchronous stochastic approximation algorithms without communication delays. Our main contribution is a stability proof for these algorithms that extends a method of Borkar and Meyn by accommodating more general noise conditions. We also derive convergence results from this stability result and discuss their application in important average-reward reinforcement learning problems.

Iterative Option Discovery for Planning, by Planning

Discovering useful temporal abstractions, in the form of options, is widely thought to be key to applying reinforcement learning and planning to increasingly complex domains. Building on the empirical success of the Expert Iteration approach to policy learning used in AlphaZero, we propose Option Iteration, an analogous approach to option discovery. Rather than learning a single strong policy that is trained to match the search results everywhere, Option Iteration learns a set of option policies trained such that for each state encountered, at least one policy in the set matches the search results for some horizon into the future. Intuitively, this may be significantly easier as it allows the algorithm to hedge its bets compared to learning a single globally strong policy, which may have complex dependencies on the details of the current state. Having learned such a set of locally strong policies, we can use them to guide the search algorithm resulting in a virtuous cycle where better options lead to better search results which allows for training of better options. We demonstrate experimentally that planning using options learned with Option Iteration leads to a significant benefit in challenging planning environments compared to an analogous planning algorithm operating in the space of primitive actions and learning a single rollout policy with Expert Iteration.

Value-aware Importance Weighting for Off-policy Reinforcement Learning

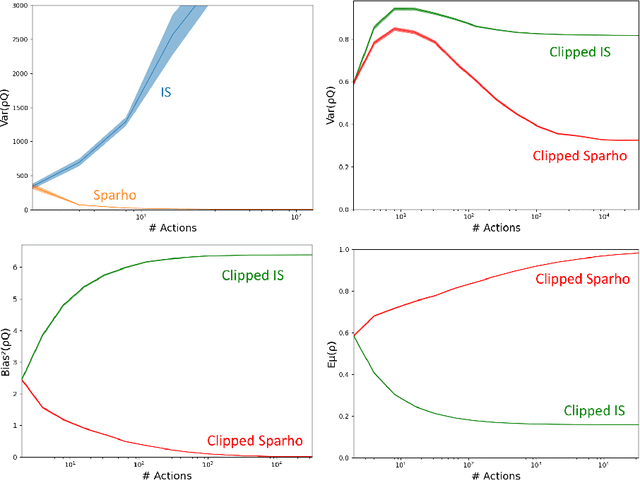
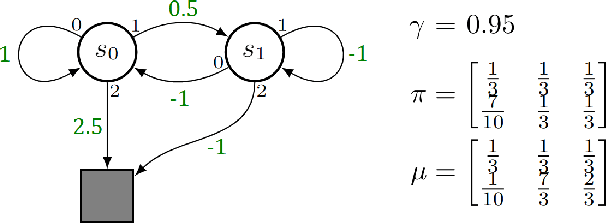
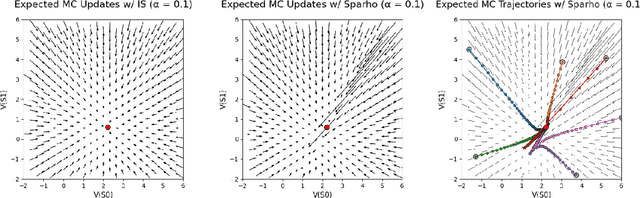
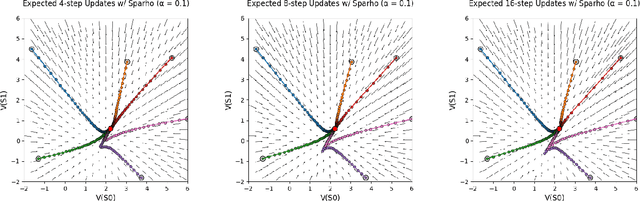
Importance sampling is a central idea underlying off-policy prediction in reinforcement learning. It provides a strategy for re-weighting samples from a distribution to obtain unbiased estimates under another distribution. However, importance sampling weights tend to exhibit extreme variance, often leading to stability issues in practice. In this work, we consider a broader class of importance weights to correct samples in off-policy learning. We propose the use of $\textit{value-aware importance weights}$ which take into account the sample space to provide lower variance, but still unbiased, estimates under a target distribution. We derive how such weights can be computed, and detail key properties of the resulting importance weights. We then extend several reinforcement learning prediction algorithms to the off-policy setting with these weights, and evaluate them empirically.

Maintaining Plasticity in Deep Continual Learning

Modern deep-learning systems are specialized to problem settings in which training occurs once and then never again, as opposed to continual-learning settings in which training occurs continually. If deep-learning systems are applied in a continual learning setting, then it is well known that they may fail catastrophically to remember earlier examples. More fundamental, but less well known, is that they may also lose their ability to adapt to new data, a phenomenon called \textit{loss of plasticity}. We show loss of plasticity using the MNIST and ImageNet datasets repurposed for continual learning as sequences of tasks. In ImageNet, binary classification performance dropped from 89% correct on an early task down to 77%, or to about the level of a linear network, on the 2000th task. Such loss of plasticity occurred with a wide range of deep network architectures, optimizers, and activation functions, and was not eased by batch normalization or dropout. In our experiments, loss of plasticity was correlated with the proliferation of dead units, with very large weights, and more generally with a loss of unit diversity. Loss of plasticity was substantially eased by $L^2$-regularization, particularly when combined with weight perturbation (Shrink and Perturb). We show that plasticity can be fully maintained by a new algorithm -- called $\textit{continual backpropagation}$ -- which is just like conventional backpropagation except that a small fraction of less-used units are reinitialized after each example.

On Convergence of Average-Reward Off-Policy Control Algorithms in Weakly-Communicating MDPs

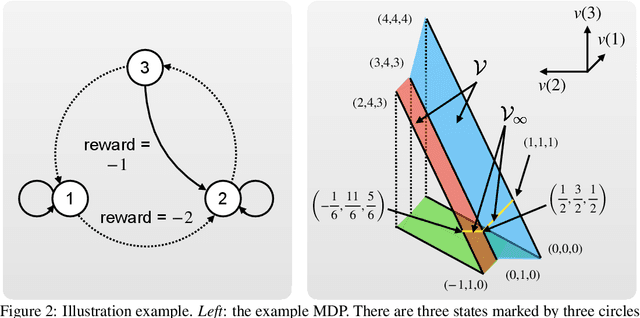
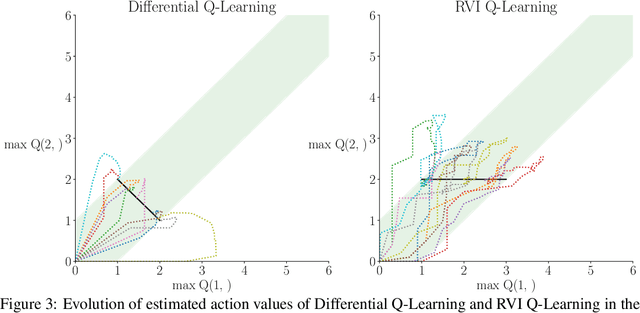
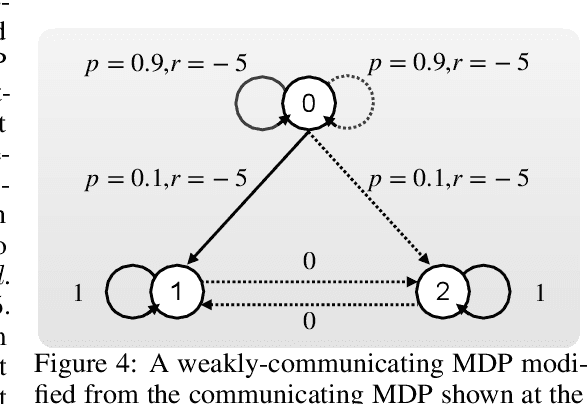
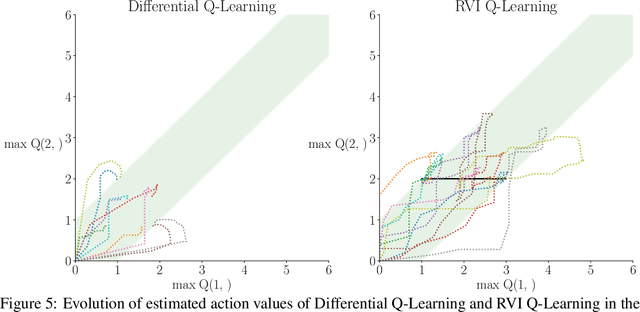
We show two average-reward off-policy control algorithms, Differential Q Learning (Wan, Naik, \& Sutton 2021a) and RVI Q Learning (Abounadi Bertsekas \& Borkar 2001), converge in weakly-communicating MDPs. Weakly-communicating MDPs are the most general class of MDPs that a learning algorithm with a single stream of experience can guarantee obtaining a policy achieving optimal reward rate. The original convergence proofs of the two algorithms require that all optimal policies induce unichains, which is not necessarily true for weakly-communicating MDPs. To the best of our knowledge, our results are the first showing average-reward off-policy control algorithms converge in weakly-communicating MDPs. As a direct extension, we show that average-reward options algorithms introduced by (Wan, Naik, \& Sutton 2021b) converge if the Semi-MDP induced by options is weakly-communicating.

The Alberta Plan for AI Research

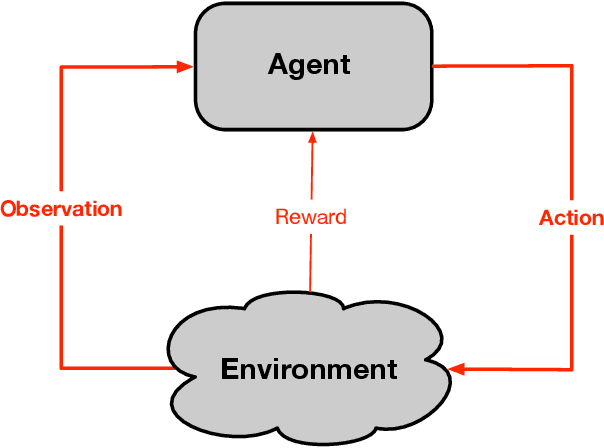
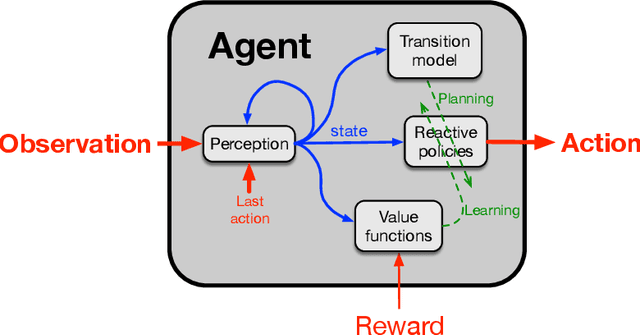
Herein we describe our approach to artificial intelligence research, which we call the Alberta Plan. The Alberta Plan is pursued within our research groups in Alberta and by others who are like minded throughout the world. We welcome all who would join us in this pursuit.