Reinitializing weights vs units for maintaining plasticity in neural networks

Loss of plasticity is a phenomenon in which a neural network loses its ability to learn when trained for an extended time on non-stationary data. It is a crucial problem to overcome when designing systems that learn continually. An effective technique for preventing loss of plasticity is reinitializing parts of the network. In this paper, we compare two different reinitialization schemes: reinitializing units vs reinitializing weights. We propose a new algorithm, which we name \textit{selective weight reinitialization}, for reinitializing the least useful weights in a network. We compare our algorithm to continual backpropagation and ReDo, two previously proposed algorithms that reinitialize units in the network. Through our experiments in continual supervised learning problems, we identify two settings when reinitializing weights is more effective at maintaining plasticity than reinitializing units: (1) when the network has a small number of units and (2) when the network includes layer normalization. Conversely, reinitializing weights and units are equally effective at maintaining plasticity when the network is of sufficient size and does not include layer normalization. We found that reinitializing weights maintains plasticity in a wider variety of settings than reinitializing units.

Maintaining Plasticity in Deep Continual Learning

Modern deep-learning systems are specialized to problem settings in which training occurs once and then never again, as opposed to continual-learning settings in which training occurs continually. If deep-learning systems are applied in a continual learning setting, then it is well known that they may fail catastrophically to remember earlier examples. More fundamental, but less well known, is that they may also lose their ability to adapt to new data, a phenomenon called \textit{loss of plasticity}. We show loss of plasticity using the MNIST and ImageNet datasets repurposed for continual learning as sequences of tasks. In ImageNet, binary classification performance dropped from 89% correct on an early task down to 77%, or to about the level of a linear network, on the 2000th task. Such loss of plasticity occurred with a wide range of deep network architectures, optimizers, and activation functions, and was not eased by batch normalization or dropout. In our experiments, loss of plasticity was correlated with the proliferation of dead units, with very large weights, and more generally with a loss of unit diversity. Loss of plasticity was substantially eased by $L^2$-regularization, particularly when combined with weight perturbation (Shrink and Perturb). We show that plasticity can be fully maintained by a new algorithm -- called $\textit{continual backpropagation}$ -- which is just like conventional backpropagation except that a small fraction of less-used units are reinitialized after each example.

Learning Sparse Representations Incrementally in Deep Reinforcement Learning

Sparse representations have been shown to be useful in deep reinforcement learning for mitigating catastrophic interference and improving the performance of agents in terms of cumulative reward. Previous results were based on a two step process were the representation was learned offline and the action-value function was learned online afterwards. In this paper, we investigate if it is possible to learn a sparse representation and the action-value function simultaneously and incrementally. We investigate this question by employing several regularization techniques and observing how they affect sparsity of the representation learned by a DQN agent in two different benchmark domains. Our results show that with appropriate regularization it is possible to increase the sparsity of the representations learned by DQN agents. Moreover, we found that learning sparse representations also resulted in improved performance in terms of cumulative reward. Finally, we found that the performance of the agents that learned a sparse representation was more robust to the size of the experience replay buffer. This last finding supports the long standing hypothesis that the overlap in representations learned by deep neural networks is the leading cause of catastrophic interference.

Understanding Multi-Step Deep Reinforcement Learning: A Systematic Study of the DQN Target

Multi-step methods such as Retrace($\lambda$) and $n$-step $Q$-learning have become a crucial component of modern deep reinforcement learning agents. These methods are often evaluated as a part of bigger architectures and their evaluations rarely include enough samples to draw statistically significant conclusions about their performance. This type of methodology makes it difficult to understand how particular algorithmic details of multi-step methods influence learning. In this paper we combine the $n$-step action-value algorithms Retrace, $Q$-learning, Tree Backup, Sarsa, and $Q(\sigma)$ with an architecture analogous to DQN. We test the performance of all these algorithms in the mountain car environment; this choice of environment allows for faster training times and larger sample sizes. We present statistical analyses on the effects of the off-policy correction, the backup length parameter $n$, and the update frequency of the target network on the performance of these algorithms. Our results show that (1) using off-policy correction can have an adverse effect on the performance of Sarsa and $Q(\sigma)$; (2) increasing the backup length $n$ consistently improved performance across all the different algorithms; and (3) the performance of Sarsa and $Q$-learning was more robust to the effect of the target network update frequency than the performance of Tree Backup, $Q(\sigma)$, and Retrace in this particular task.

Multi-step Reinforcement Learning: A Unifying Algorithm

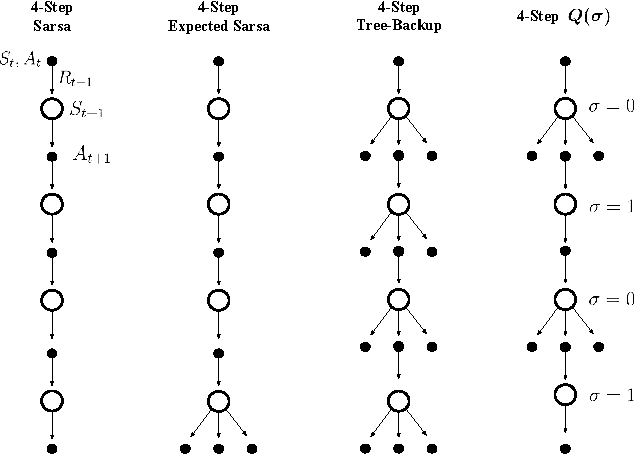
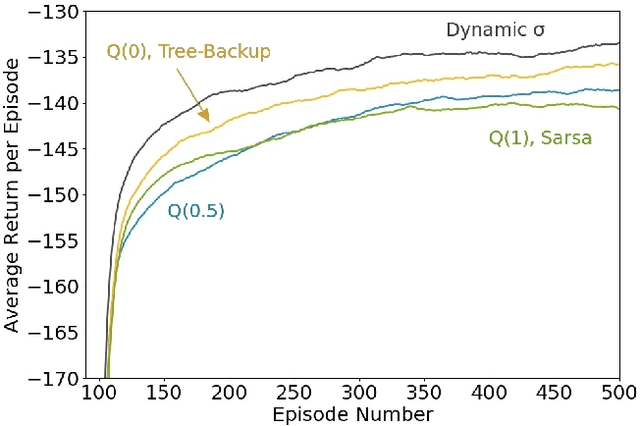
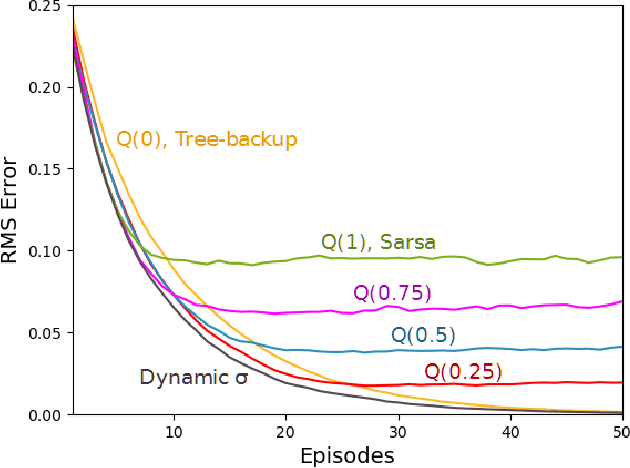
Unifying seemingly disparate algorithmic ideas to produce better performing algorithms has been a longstanding goal in reinforcement learning. As a primary example, TD($\lambda$) elegantly unifies one-step TD prediction with Monte Carlo methods through the use of eligibility traces and the trace-decay parameter $\lambda$. Currently, there are a multitude of algorithms that can be used to perform TD control, including Sarsa, $Q$-learning, and Expected Sarsa. These methods are often studied in the one-step case, but they can be extended across multiple time steps to achieve better performance. Each of these algorithms is seemingly distinct, and no one dominates the others for all problems. In this paper, we study a new multi-step action-value algorithm called $Q(\sigma)$ which unifies and generalizes these existing algorithms, while subsuming them as special cases. A new parameter, $\sigma$, is introduced to allow the degree of sampling performed by the algorithm at each step during its backup to be continuously varied, with Sarsa existing at one extreme (full sampling), and Expected Sarsa existing at the other (pure expectation). $Q(\sigma)$ is generally applicable to both on- and off-policy learning, but in this work we focus on experiments in the on-policy case. Our results show that an intermediate value of $\sigma$, which results in a mixture of the existing algorithms, performs better than either extreme. The mixture can also be varied dynamically which can result in even greater performance.