Reinitializing weights vs units for maintaining plasticity in neural networks

Loss of plasticity is a phenomenon in which a neural network loses its ability to learn when trained for an extended time on non-stationary data. It is a crucial problem to overcome when designing systems that learn continually. An effective technique for preventing loss of plasticity is reinitializing parts of the network. In this paper, we compare two different reinitialization schemes: reinitializing units vs reinitializing weights. We propose a new algorithm, which we name \textit{selective weight reinitialization}, for reinitializing the least useful weights in a network. We compare our algorithm to continual backpropagation and ReDo, two previously proposed algorithms that reinitialize units in the network. Through our experiments in continual supervised learning problems, we identify two settings when reinitializing weights is more effective at maintaining plasticity than reinitializing units: (1) when the network has a small number of units and (2) when the network includes layer normalization. Conversely, reinitializing weights and units are equally effective at maintaining plasticity when the network is of sufficient size and does not include layer normalization. We found that reinitializing weights maintains plasticity in a wider variety of settings than reinitializing units.

Maintaining Plasticity in Deep Continual Learning

Modern deep-learning systems are specialized to problem settings in which training occurs once and then never again, as opposed to continual-learning settings in which training occurs continually. If deep-learning systems are applied in a continual learning setting, then it is well known that they may fail catastrophically to remember earlier examples. More fundamental, but less well known, is that they may also lose their ability to adapt to new data, a phenomenon called \textit{loss of plasticity}. We show loss of plasticity using the MNIST and ImageNet datasets repurposed for continual learning as sequences of tasks. In ImageNet, binary classification performance dropped from 89% correct on an early task down to 77%, or to about the level of a linear network, on the 2000th task. Such loss of plasticity occurred with a wide range of deep network architectures, optimizers, and activation functions, and was not eased by batch normalization or dropout. In our experiments, loss of plasticity was correlated with the proliferation of dead units, with very large weights, and more generally with a loss of unit diversity. Loss of plasticity was substantially eased by $L^2$-regularization, particularly when combined with weight perturbation (Shrink and Perturb). We show that plasticity can be fully maintained by a new algorithm -- called $\textit{continual backpropagation}$ -- which is just like conventional backpropagation except that a small fraction of less-used units are reinitialized after each example.

Automatic Noise Filtering with Dynamic Sparse Training in Deep Reinforcement Learning

Tomorrow's robots will need to distinguish useful information from noise when performing different tasks. A household robot for instance may continuously receive a plethora of information about the home, but needs to focus on just a small subset to successfully execute its current chore. Filtering distracting inputs that contain irrelevant data has received little attention in the reinforcement learning literature. To start resolving this, we formulate a problem setting in reinforcement learning called the $\textit{extremely noisy environment}$ (ENE), where up to $99\%$ of the input features are pure noise. Agents need to detect which features provide task-relevant information about the state of the environment. Consequently, we propose a new method termed $\textit{Automatic Noise Filtering}$ (ANF), which uses the principles of dynamic sparse training in synergy with various deep reinforcement learning algorithms. The sparse input layer learns to focus its connectivity on task-relevant features, such that ANF-SAC and ANF-TD3 outperform standard SAC and TD3 by a large margin, while using up to $95\%$ fewer weights. Furthermore, we devise a transfer learning setting for ENEs, by permuting all features of the environment after 1M timesteps to simulate the fact that other information sources can become relevant as the world evolves. Again, ANF surpasses the baselines in final performance and sample complexity. Our code is available at https://github.com/bramgrooten/automatic-noise-filtering

Continual Backprop: Stochastic Gradient Descent with Persistent Randomness

The Backprop algorithm for learning in neural networks utilizes two mechanisms: first, stochastic gradient descent and second, initialization with small random weights, where the latter is essential to the effectiveness of the former. We show that in continual learning setups, Backprop performs well initially, but over time its performance degrades. Stochastic gradient descent alone is insufficient to learn continually; the initial randomness enables only initial learning but not continual learning. To the best of our knowledge, ours is the first result showing this degradation in Backprop's ability to learn. To address this issue, we propose an algorithm that continually injects random features alongside gradient descent using a new generate-and-test process. We call this the Continual Backprop algorithm. We show that, unlike Backprop, Continual Backprop is able to continually adapt in both supervised and reinforcement learning problems. We expect that as continual learning becomes more common in future applications, a method like Continual Backprop will be essential where the advantages of random initialization are present throughout learning.

Gamma-Nets: Generalizing Value Estimation over Timescale

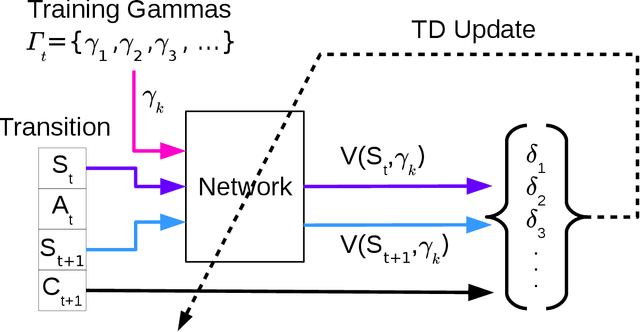
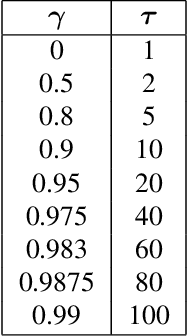
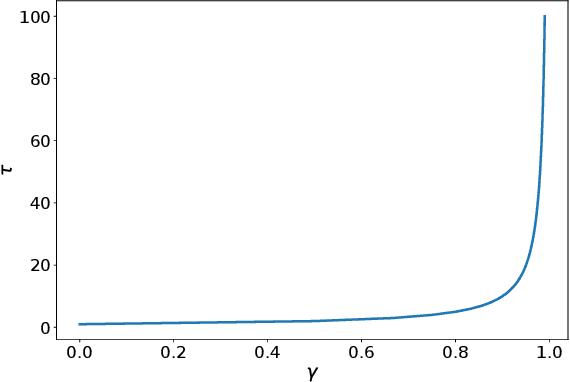
We present $\Gamma$-nets, a method for generalizing value function estimation over timescale. By using the timescale as one of the estimator's inputs we can estimate value for arbitrary timescales. As a result, the prediction target for any timescale is available and we are free to train on multiple timescales at each timestep. Here we empirically evaluate $\Gamma$-nets in the policy evaluation setting. We first demonstrate the approach on a square wave and then on a robot arm using linear function approximation. Next, we consider the deep reinforcement learning setting using several Atari video games. Our results show that $\Gamma$-nets can be effective for predicting arbitrary timescales, with only a small cost in accuracy as compared to learning estimators for fixed timescales. $\Gamma$-nets provide a method for compactly making predictions at many timescales without requiring a priori knowledge of the task, making it a valuable contribution to ongoing work on model-based planning, representation learning, and lifelong learning algorithms.

Text Summarization using Abstract Meaning Representation

With an ever increasing size of text present on the Internet, automatic summary generation remains an important problem for natural language understanding. In this work we explore a novel full-fledged pipeline for text summarization with an intermediate step of Abstract Meaning Representation (AMR). The pipeline proposed by us first generates an AMR graph of an input story, through which it extracts a summary graph and finally, generate summary sentences from this summary graph. Our proposed method achieves state-of-the-art results compared to the other text summarization routines based on AMR. We also point out some significant problems in the existing evaluation methods, which make them unsuitable for evaluating summary quality.

Variational Inference via Transformations on Distributions

Variational inference methods often focus on the problem of efficient model optimization, with little emphasis on the choice of the approximating posterior. In this paper, we review and implement the various methods that enable us to develop a rich family of approximating posteriors. We show that one particular method employing transformations on distributions results in developing very rich and complex posterior approximation. We analyze its performance on the MNIST dataset by implementing with a Variational Autoencoder and demonstrate its effectiveness in learning better posterior distributions.