sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

A Practical Guide to Statistical Distances for Evaluating Generative Models in Science

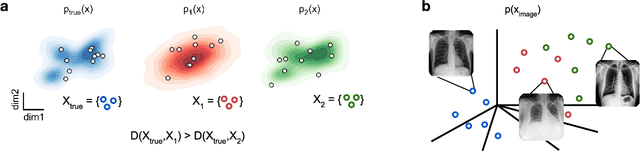
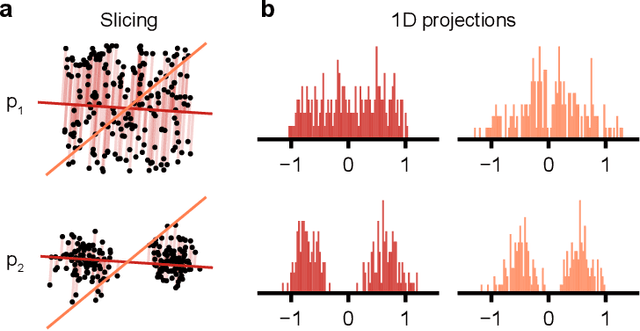
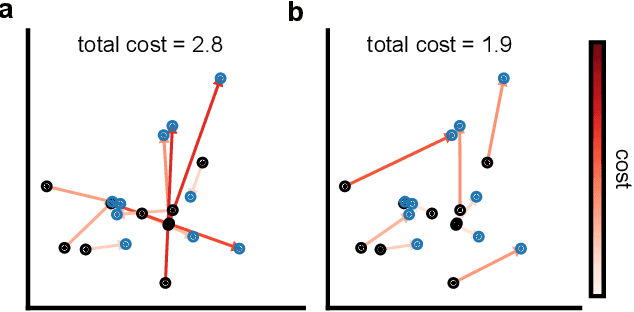
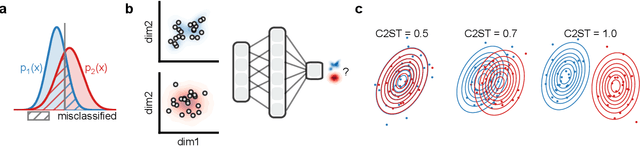
Generative models are invaluable in many fields of science because of their ability to capture high-dimensional and complicated distributions, such as photo-realistic images, protein structures, and connectomes. How do we evaluate the samples these models generate? This work aims to provide an accessible entry point to understanding popular notions of statistical distances, requiring only foundational knowledge in mathematics and statistics. We focus on four commonly used notions of statistical distances representing different methodologies: Using low-dimensional projections (Sliced-Wasserstein; SW), obtaining a distance using classifiers (Classifier Two-Sample Tests; C2ST), using embeddings through kernels (Maximum Mean Discrepancy; MMD), or neural networks (Fr\'echet Inception Distance; FID). We highlight the intuition behind each distance and explain their merits, scalability, complexity, and pitfalls. To demonstrate how these distances are used in practice, we evaluate generative models from different scientific domains, namely a model of decision making and a model generating medical images. We showcase that distinct distances can give different results on similar data. Through this guide, we aim to help researchers to use, interpret, and evaluate statistical distances for generative models in science.

Unsupervised Anomaly Detection using Aggregated Normative Diffusion

Early detection of anomalies in medical images such as brain MRI is highly relevant for diagnosis and treatment of many conditions. Supervised machine learning methods are limited to a small number of pathologies where there is good availability of labeled data. In contrast, unsupervised anomaly detection (UAD) has the potential to identify a broader spectrum of anomalies by spotting deviations from normal patterns. Our research demonstrates that existing state-of-the-art UAD approaches do not generalise well to diverse types of anomalies in realistic multi-modal MR data. To overcome this, we introduce a new UAD method named Aggregated Normative Diffusion (ANDi). ANDi operates by aggregating differences between predicted denoising steps and ground truth backwards transitions in Denoising Diffusion Probabilistic Models (DDPMs) that have been trained on pyramidal Gaussian noise. We validate ANDi against three recent UAD baselines, and across three diverse brain MRI datasets. We show that ANDi, in some cases, substantially surpasses these baselines and shows increased robustness to varying types of anomalies. Particularly in detecting multiple sclerosis (MS) lesions, ANDi achieves improvements of up to 178% in terms of AUPRC.

Multiscale Metamorphic VAE for 3D Brain MRI Synthesis

Generative modeling of 3D brain MRIs presents difficulties in achieving high visual fidelity while ensuring sufficient coverage of the data distribution. In this work, we propose to address this challenge with composable, multiscale morphological transformations in a variational autoencoder (VAE) framework. These transformations are applied to a chosen reference brain image to generate MRI volumes, equipping the model with strong anatomical inductive biases. We structure the VAE latent space in a way such that the model covers the data distribution sufficiently well. We show substantial performance improvements in FID while retaining comparable, or superior, reconstruction quality compared to prior work based on VAEs and generative adversarial networks (GANs).

Variational Inference via Transformations on Distributions

Variational inference methods often focus on the problem of efficient model optimization, with little emphasis on the choice of the approximating posterior. In this paper, we review and implement the various methods that enable us to develop a rich family of approximating posteriors. We show that one particular method employing transformations on distributions results in developing very rich and complex posterior approximation. We analyze its performance on the MNIST dataset by implementing with a Variational Autoencoder and demonstrate its effectiveness in learning better posterior distributions.