sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

GATSBI: Generative Adversarial Training for Simulation-Based Inference

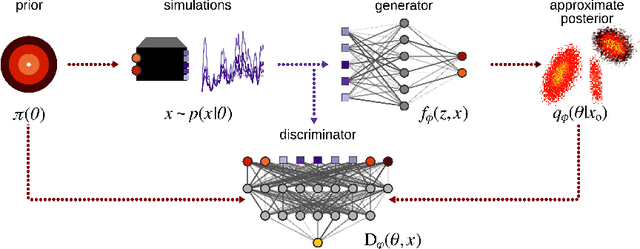
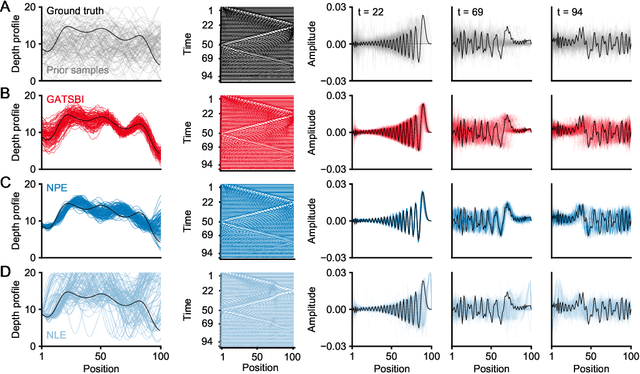
Simulation-based inference (SBI) refers to statistical inference on stochastic models for which we can generate samples, but not compute likelihoods. Like SBI algorithms, generative adversarial networks (GANs) do not require explicit likelihoods. We study the relationship between SBI and GANs, and introduce GATSBI, an adversarial approach to SBI. GATSBI reformulates the variational objective in an adversarial setting to learn implicit posterior distributions. Inference with GATSBI is amortised across observations, works in high-dimensional posterior spaces and supports implicit priors. We evaluate GATSBI on two SBI benchmark problems and on two high-dimensional simulators. On a model for wave propagation on the surface of a shallow water body, we show that GATSBI can return well-calibrated posterior estimates even in high dimensions. On a model of camera optics, it infers a high-dimensional posterior given an implicit prior, and performs better than a state-of-the-art SBI approach. We also show how GATSBI can be extended to perform sequential posterior estimation to focus on individual observations. Overall, GATSBI opens up opportunities for leveraging advances in GANs to perform Bayesian inference on high-dimensional simulation-based models.

Benchmarking Simulation-Based Inference

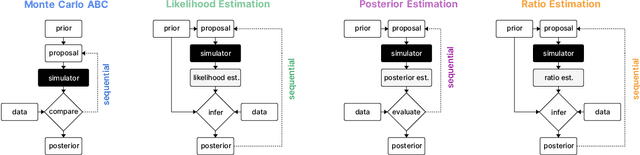
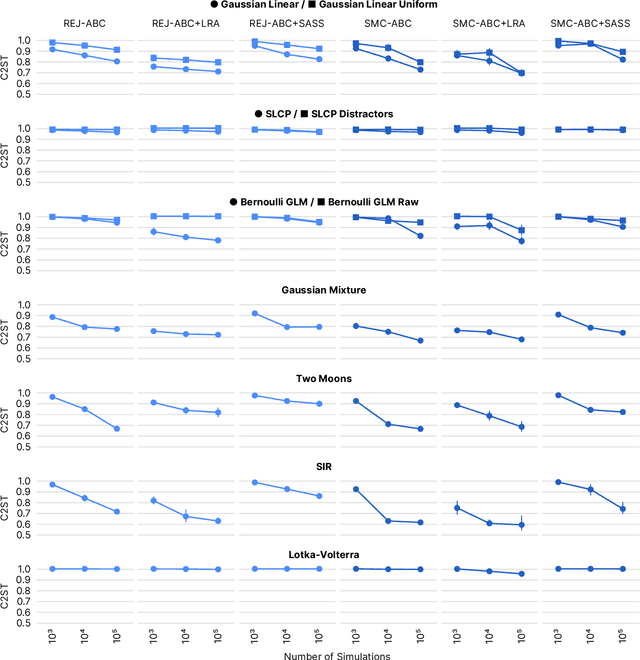
Recent advances in probabilistic modelling have led to a large number of simulation-based inference algorithms which do not require numerical evaluation of likelihoods. However, a public benchmark with appropriate performance metrics for such 'likelihood-free' algorithms has been lacking. This has made it difficult to compare algorithms and identify their strengths and weaknesses. We set out to fill this gap: We provide a benchmark with inference tasks and suitable performance metrics, with an initial selection of algorithms including recent approaches employing neural networks and classical Approximate Bayesian Computation methods. We found that the choice of performance metric is critical, that even state-of-the-art algorithms have substantial room for improvement, and that sequential estimation improves sample efficiency. Neural network-based approaches generally exhibit better performance, but there is no uniformly best algorithm. We provide practical advice and highlight the potential of the benchmark to diagnose problems and improve algorithms. The results can be explored interactively on a companion website. All code is open source, making it possible to contribute further benchmark tasks and inference algorithms.

SBI -- A toolkit for simulation-based inference

Scientists and engineers employ stochastic numerical simulators to model empirically observed phenomena. In contrast to purely statistical models, simulators express scientific principles that provide powerful inductive biases, improve generalization to new data or scenarios and allow for fewer, more interpretable and domain-relevant parameters. Despite these advantages, tuning a simulator's parameters so that its outputs match data is challenging. Simulation-based inference (SBI) seeks to identify parameter sets that a) are compatible with prior knowledge and b) match empirical observations. Importantly, SBI does not seek to recover a single 'best' data-compatible parameter set, but rather to identify all high probability regions of parameter space that explain observed data, and thereby to quantify parameter uncertainty. In Bayesian terminology, SBI aims to retrieve the posterior distribution over the parameters of interest. In contrast to conventional Bayesian inference, SBI is also applicable when one can run model simulations, but no formula or algorithm exists for evaluating the probability of data given parameters, i.e. the likelihood. We present $\texttt{sbi}$, a PyTorch-based package that implements SBI algorithms based on neural networks. $\texttt{sbi}$ facilitates inference on black-box simulators for practising scientists and engineers by providing a unified interface to state-of-the-art algorithms together with documentation and tutorials.

Likelihood-free inference with emulator networks

Approximate Bayesian Computation (ABC) provides methods for Bayesian inference in simulation-based stochastic models which do not permit tractable likelihoods. We present a new ABC method which uses probabilistic neural emulator networks to learn synthetic likelihoods on simulated data -- both local emulators which approximate the likelihood for specific observed data, as well as global ones which are applicable to a range of data. Simulations are chosen adaptively using an acquisition function which takes into account uncertainty about either the posterior distribution of interest, or the parameters of the emulator. Our approach does not rely on user-defined rejection thresholds or distance functions. We illustrate inference with emulator networks on synthetic examples and on a biophysical neuron model, and show that emulators allow accurate and efficient inference even on high-dimensional problems which are challenging for conventional ABC approaches.

Flexible statistical inference for mechanistic models of neural dynamics

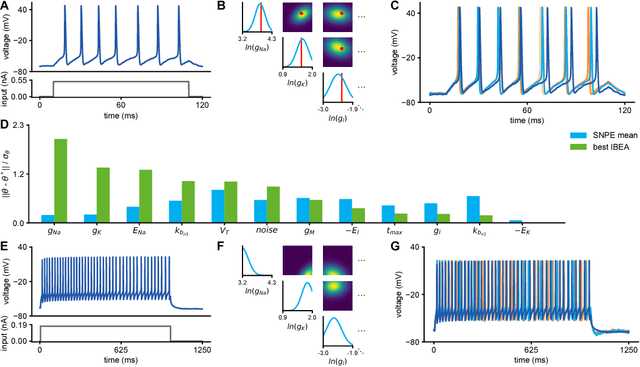
Mechanistic models of single-neuron dynamics have been extensively studied in computational neuroscience. However, identifying which models can quantitatively reproduce empirically measured data has been challenging. We propose to overcome this limitation by using likelihood-free inference approaches (also known as Approximate Bayesian Computation, ABC) to perform full Bayesian inference on single-neuron models. Our approach builds on recent advances in ABC by learning a neural network which maps features of the observed data to the posterior distribution over parameters. We learn a Bayesian mixture-density network approximating the posterior over multiple rounds of adaptively chosen simulations. Furthermore, we propose an efficient approach for handling missing features and parameter settings for which the simulator fails, as well as a strategy for automatically learning relevant features using recurrent neural networks. On synthetic data, our approach efficiently estimates posterior distributions and recovers ground-truth parameters. On in-vitro recordings of membrane voltages, we recover multivariate posteriors over biophysical parameters, which yield model-predicted voltage traces that accurately match empirical data. Our approach will enable neuroscientists to perform Bayesian inference on complex neuron models without having to design model-specific algorithms, closing the gap between mechanistic and statistical approaches to single-neuron modelling.