GATSBI: Generative Adversarial Training for Simulation-Based Inference
Paper and Code
Mar 12, 2022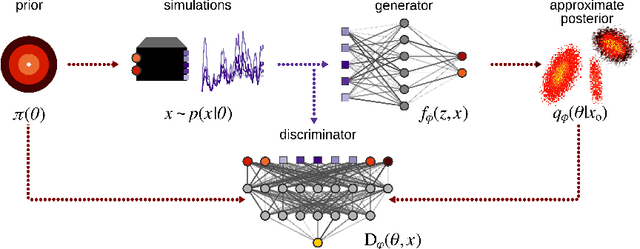


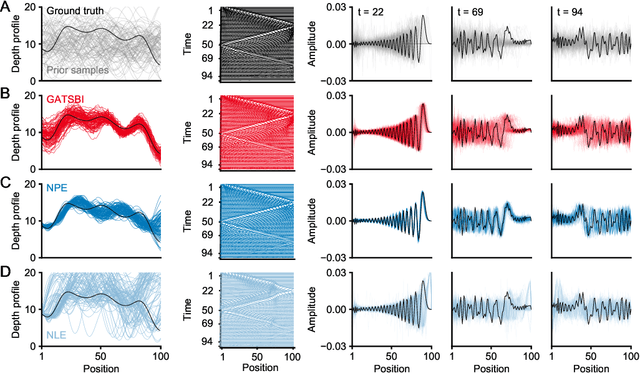
Simulation-based inference (SBI) refers to statistical inference on stochastic models for which we can generate samples, but not compute likelihoods. Like SBI algorithms, generative adversarial networks (GANs) do not require explicit likelihoods. We study the relationship between SBI and GANs, and introduce GATSBI, an adversarial approach to SBI. GATSBI reformulates the variational objective in an adversarial setting to learn implicit posterior distributions. Inference with GATSBI is amortised across observations, works in high-dimensional posterior spaces and supports implicit priors. We evaluate GATSBI on two SBI benchmark problems and on two high-dimensional simulators. On a model for wave propagation on the surface of a shallow water body, we show that GATSBI can return well-calibrated posterior estimates even in high dimensions. On a model of camera optics, it infers a high-dimensional posterior given an implicit prior, and performs better than a state-of-the-art SBI approach. We also show how GATSBI can be extended to perform sequential posterior estimation to focus on individual observations. Overall, GATSBI opens up opportunities for leveraging advances in GANs to perform Bayesian inference on high-dimensional simulation-based models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge