Jakob H. Macke
Computational Neuroengineering, Department of Electrical and Computer Engineering, Technical University of Munich, Machine Learning in Science, University of Tübingen, Empirical Inference, Max Planck Institute for Intelligent Systems, Tübingen
MRExtrap: Longitudinal Aging of Brain MRIs using Linear Modeling in Latent Space
Aug 26, 2025Abstract:Simulating aging in 3D brain MRI scans can reveal disease progression patterns in neurological disorders such as Alzheimer's disease. Current deep learning-based generative models typically approach this problem by predicting future scans from a single observed scan. We investigate modeling brain aging via linear models in the latent space of convolutional autoencoders (MRExtrap). Our approach, MRExtrap, is based on our observation that autoencoders trained on brain MRIs create latent spaces where aging trajectories appear approximately linear. We train autoencoders on brain MRIs to create latent spaces, and investigate how these latent spaces allow predicting future MRIs through linear extrapolation based on age, using an estimated latent progression rate $\boldsymbol{\beta}$. For single-scan prediction, we propose using population-averaged and subject-specific priors on linear progression rates. We also demonstrate that predictions in the presence of additional scans can be flexibly updated using Bayesian posterior sampling, providing a mechanism for subject-specific refinement. On the ADNI dataset, MRExtrap predicts aging patterns accurately and beats a GAN-based baseline for single-volume prediction of brain aging. We also demonstrate and analyze multi-scan conditioning to incorporate subject-specific progression rates. Finally, we show that the latent progression rates in MRExtrap's linear framework correlate with disease and age-based aging patterns from previously studied structural atrophy rates. MRExtrap offers a simple and robust method for the age-based generation of 3D brain MRIs, particularly valuable in scenarios with multiple longitudinal observations.
FNOPE: Simulation-based inference on function spaces with Fourier Neural Operators
May 28, 2025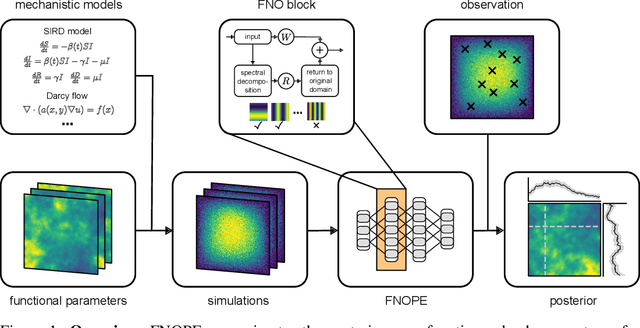
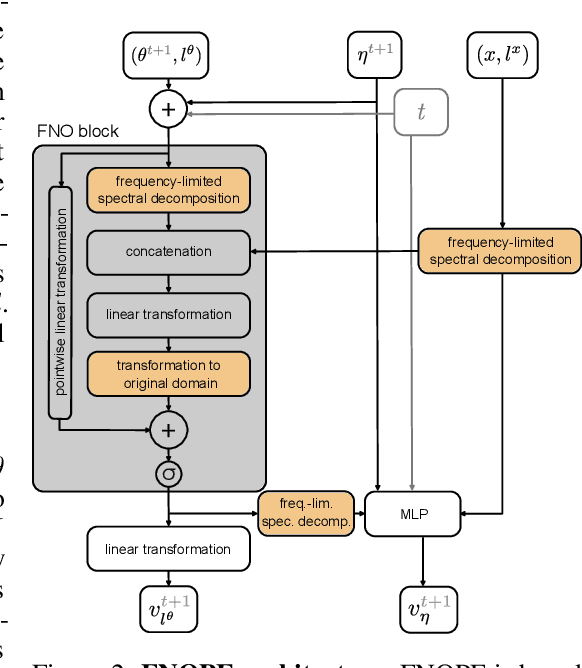


Abstract:Simulation-based inference (SBI) is an established approach for performing Bayesian inference on scientific simulators. SBI so far works best on low-dimensional parametric models. However, it is difficult to infer function-valued parameters, which frequently occur in disciplines that model spatiotemporal processes such as the climate and earth sciences. Here, we introduce an approach for efficient posterior estimation, using a Fourier Neural Operator (FNO) architecture with a flow matching objective. We show that our approach, FNOPE, can perform inference of function-valued parameters at a fraction of the simulation budget of state of the art methods. In addition, FNOPE supports posterior evaluation at arbitrary discretizations of the domain, as well as simultaneous estimation of vector-valued parameters. We demonstrate the effectiveness of our approach on several benchmark tasks and a challenging spatial inference task from glaciology. FNOPE extends the applicability of SBI methods to new scientific domains by enabling the inference of function-valued parameters.
Effortless, Simulation-Efficient Bayesian Inference using Tabular Foundation Models
Apr 24, 2025Abstract:Simulation-based inference (SBI) offers a flexible and general approach to performing Bayesian inference: In SBI, a neural network is trained on synthetic data simulated from a model and used to rapidly infer posterior distributions for observed data. A key goal for SBI is to achieve accurate inference with as few simulations as possible, especially for expensive simulators. In this work, we address this challenge by repurposing recent probabilistic foundation models for tabular data: We show how tabular foundation models -- specifically TabPFN -- can be used as pre-trained autoregressive conditional density estimators for SBI. We propose Neural Posterior Estimation with Prior-data Fitted Networks (NPE-PF) and show that it is competitive with current SBI approaches in terms of accuracy for both benchmark tasks and two complex scientific inverse problems. Crucially, it often substantially outperforms them in terms of simulation efficiency, sometimes requiring orders of magnitude fewer simulations. NPE-PF eliminates the need for inference network selection, training, and hyperparameter tuning. We also show that it exhibits superior robustness to model misspecification and can be scaled to simulation budgets that exceed the context size limit of TabPFN. NPE-PF provides a new direction for SBI, where training-free, general-purpose inference models offer efficient, easy-to-use, and flexible solutions for a wide range of stochastic inverse problems.
sbi reloaded: a toolkit for simulation-based inference workflows
Nov 26, 2024
Abstract:Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.
Compositional simulation-based inference for time series
Nov 05, 2024Abstract:Amortized simulation-based inference (SBI) methods train neural networks on simulated data to perform Bayesian inference. While this approach avoids the need for tractable likelihoods, it often requires a large number of simulations and has been challenging to scale to time-series data. Scientific simulators frequently emulate real-world dynamics through thousands of single-state transitions over time. We propose an SBI framework that can exploit such Markovian simulators by locally identifying parameters consistent with individual state transitions. We then compose these local results to obtain a posterior over parameters that align with the entire time series observation. We focus on applying this approach to neural posterior score estimation but also show how it can be applied, e.g., to neural likelihood (ratio) estimation. We demonstrate that our approach is more simulation-efficient than directly estimating the global posterior on several synthetic benchmark tasks and simulators used in ecology and epidemiology. Finally, we validate scalability and simulation efficiency of our approach by applying it to a high-dimensional Kolmogorov flow simulator with around one million dimensions in the data domain.
Neural timescales from a computational perspective
Sep 04, 2024



Abstract:Timescales of neural activity are diverse across and within brain areas, and experimental observations suggest that neural timescales reflect information in dynamic environments. However, these observations do not specify how neural timescales are shaped, nor whether particular timescales are necessary for neural computations and brain function. Here, we take a complementary perspective and synthesize three directions where computational methods can distill the broad set of empirical observations into quantitative and testable theories: We review (i) how data analysis methods allow us to capture different timescales of neural dynamics across different recording modalities, (ii) how computational models provide a mechanistic explanation for the emergence of diverse timescales, and (iii) how task-optimized models in machine learning uncover the functional relevance of neural timescales. This integrative computational approach, combined with empirical findings, would provide a more holistic understanding of how neural timescales capture the relationship between brain structure, dynamics, and behavior.
Real-time gravitational-wave inference for binary neutron stars using machine learning
Jul 12, 2024



Abstract:Mergers of binary neutron stars (BNSs) emit signals in both the gravitational-wave (GW) and electromagnetic (EM) spectra. Famously, the 2017 multi-messenger observation of GW170817 led to scientific discoveries across cosmology, nuclear physics, and gravity. Central to these results were the sky localization and distance obtained from GW data, which, in the case of GW170817, helped to identify the associated EM transient, AT 2017gfo, 11 hours after the GW signal. Fast analysis of GW data is critical for directing time-sensitive EM observations; however, due to challenges arising from the length and complexity of signals, it is often necessary to make approximations that sacrifice accuracy. Here, we develop a machine learning approach that performs complete BNS inference in just one second without making any such approximations. This is enabled by a new method for explicit integration of physical domain knowledge into neural networks. Our approach enhances multi-messenger observations by providing (i) accurate localization even before the merger; (ii) improved localization precision by $\sim30\%$ compared to approximate low-latency methods; and (iii) detailed information on luminosity distance, inclination, and masses, which can be used to prioritize expensive telescope time. Additionally, the flexibility and reduced cost of our method open new opportunities for equation-of-state and waveform systematics studies. Finally, we demonstrate that our method scales to extremely long signals, up to an hour in length, thus serving as a blueprint for data analysis for next-generation ground- and space-based detectors.
All-in-one simulation-based inference
Apr 15, 2024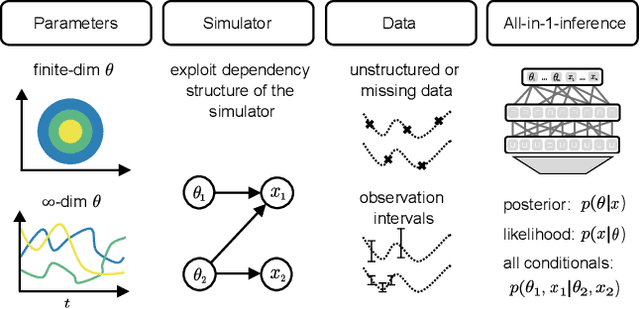
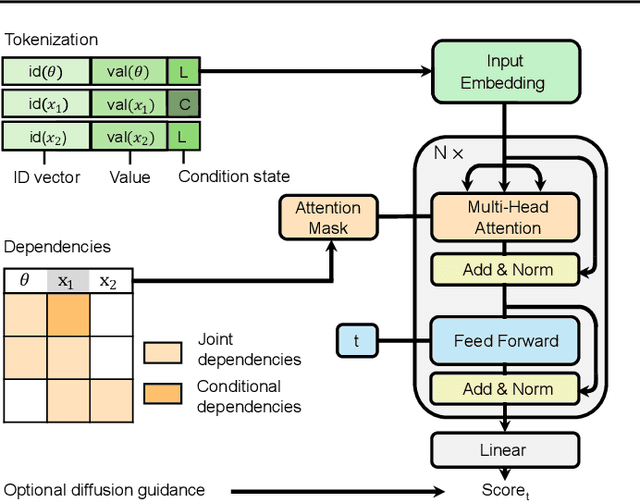
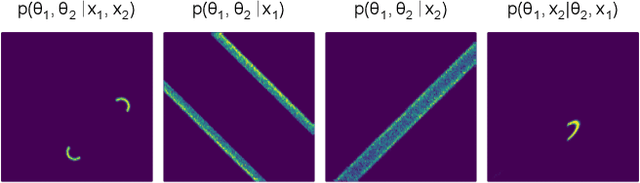
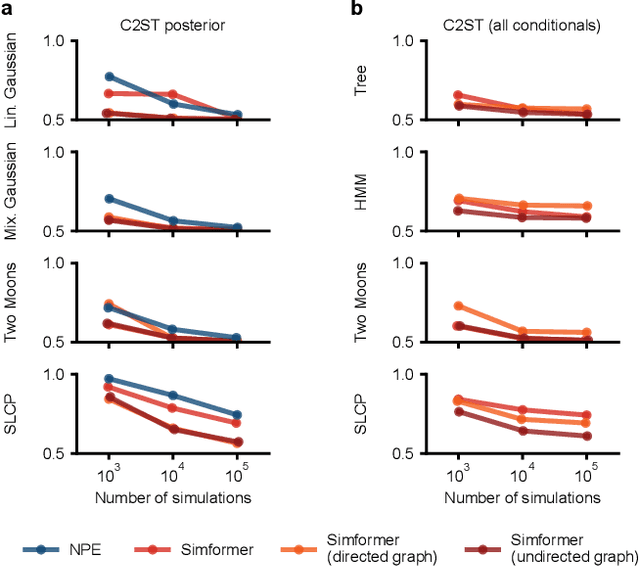
Abstract:Amortized Bayesian inference trains neural networks to solve stochastic inference problems using model simulations, thereby making it possible to rapidly perform Bayesian inference for any newly observed data. However, current simulation-based amortized inference methods are simulation-hungry and inflexible: They require the specification of a fixed parametric prior, simulator, and inference tasks ahead of time. Here, we present a new amortized inference method -- the Simformer -- which overcomes these limitations. By training a probabilistic diffusion model with transformer architectures, the Simformer outperforms current state-of-the-art amortized inference approaches on benchmark tasks and is substantially more flexible: It can be applied to models with function-valued parameters, it can handle inference scenarios with missing or unstructured data, and it can sample arbitrary conditionals of the joint distribution of parameters and data, including both posterior and likelihood. We showcase the performance and flexibility of the Simformer on simulators from ecology, epidemiology, and neuroscience, and demonstrate that it opens up new possibilities and application domains for amortized Bayesian inference on simulation-based models.
Diffusion Tempering Improves Parameter Estimation with Probabilistic Integrators for Ordinary Differential Equations
Feb 19, 2024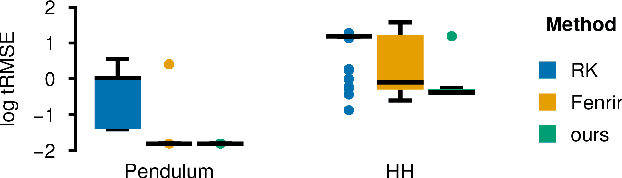
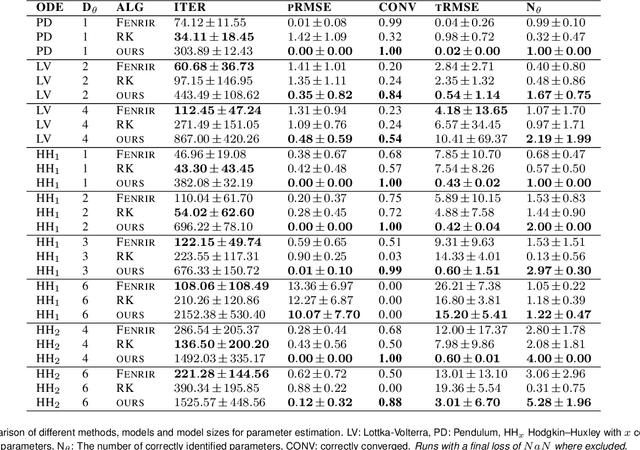
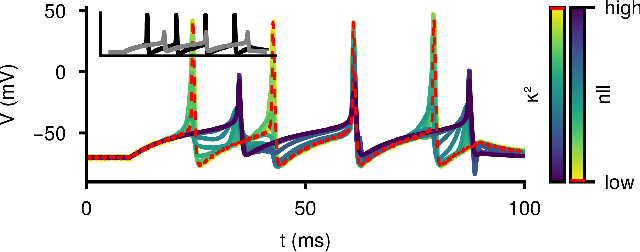

Abstract:Ordinary differential equations (ODEs) are widely used to describe dynamical systems in science, but identifying parameters that explain experimental measurements is challenging. In particular, although ODEs are differentiable and would allow for gradient-based parameter optimization, the nonlinear dynamics of ODEs often lead to many local minima and extreme sensitivity to initial conditions. We therefore propose diffusion tempering, a novel regularization technique for probabilistic numerical methods which improves convergence of gradient-based parameter optimization in ODEs. By iteratively reducing a noise parameter of the probabilistic integrator, the proposed method converges more reliably to the true parameters. We demonstrate that our method is effective for dynamical systems of different complexity and show that it obtains reliable parameter estimates for a Hodgkin-Huxley model with a practically relevant number of parameters.
Sourcerer: Sample-based Maximum Entropy Source Distribution Estimation
Feb 12, 2024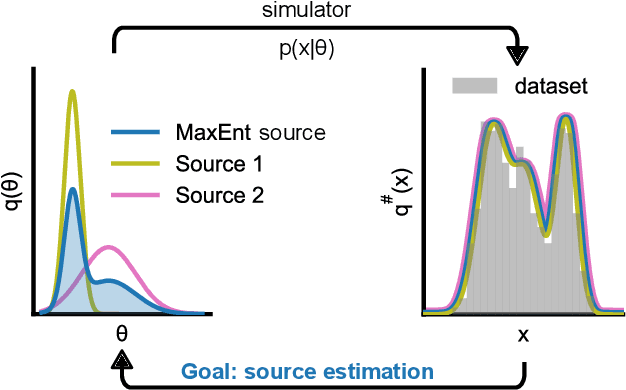
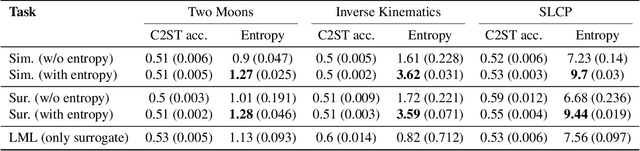

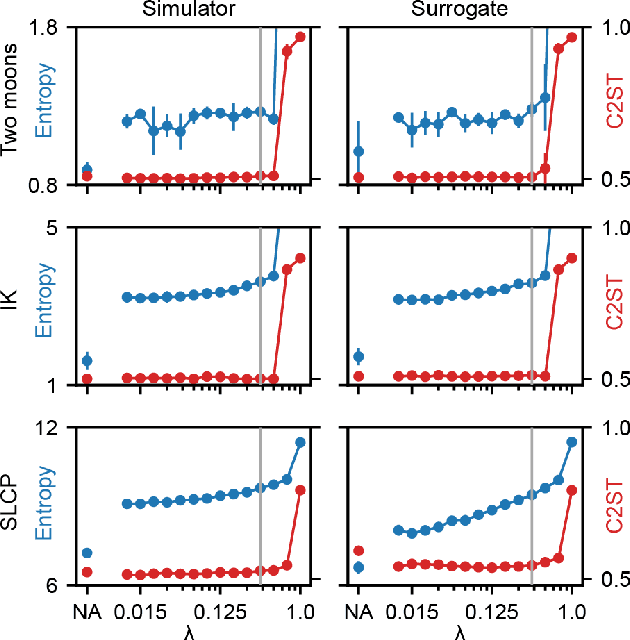
Abstract:Scientific modeling applications often require estimating a distribution of parameters consistent with a dataset of observations - an inference task also known as source distribution estimation. This problem can be ill-posed, however, since many different source distributions might produce the same distribution of data-consistent simulations. To make a principled choice among many equally valid sources, we propose an approach which targets the maximum entropy distribution, i.e., prioritizes retaining as much uncertainty as possible. Our method is purely sample-based - leveraging the Sliced-Wasserstein distance to measure the discrepancy between the dataset and simulations - and thus suitable for simulators with intractable likelihoods. We benchmark our method on several tasks, and show that it can recover source distributions with substantially higher entropy without sacrificing the fidelity of the simulations. Finally, to demonstrate the utility of our approach, we infer source distributions for parameters of the Hodgkin-Huxley neuron model from experimental datasets with thousands of measurements. In summary, we propose a principled framework for inferring unique source distributions of scientific simulator parameters while retaining as much uncertainty as possible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge