Real-time gravitational-wave inference for binary neutron stars using machine learning

Mergers of binary neutron stars (BNSs) emit signals in both the gravitational-wave (GW) and electromagnetic (EM) spectra. Famously, the 2017 multi-messenger observation of GW170817 led to scientific discoveries across cosmology, nuclear physics, and gravity. Central to these results were the sky localization and distance obtained from GW data, which, in the case of GW170817, helped to identify the associated EM transient, AT 2017gfo, 11 hours after the GW signal. Fast analysis of GW data is critical for directing time-sensitive EM observations; however, due to challenges arising from the length and complexity of signals, it is often necessary to make approximations that sacrifice accuracy. Here, we develop a machine learning approach that performs complete BNS inference in just one second without making any such approximations. This is enabled by a new method for explicit integration of physical domain knowledge into neural networks. Our approach enhances multi-messenger observations by providing (i) accurate localization even before the merger; (ii) improved localization precision by $\sim30\%$ compared to approximate low-latency methods; and (iii) detailed information on luminosity distance, inclination, and masses, which can be used to prioritize expensive telescope time. Additionally, the flexibility and reduced cost of our method open new opportunities for equation-of-state and waveform systematics studies. Finally, we demonstrate that our method scales to extremely long signals, up to an hour in length, thus serving as a blueprint for data analysis for next-generation ground- and space-based detectors.

Adapting to noise distribution shifts in flow-based gravitational-wave inference

Deep learning techniques for gravitational-wave parameter estimation have emerged as a fast alternative to standard samplers $\unicode{x2013}$ producing results of comparable accuracy. These approaches (e.g., DINGO) enable amortized inference by training a normalizing flow to represent the Bayesian posterior conditional on observed data. By conditioning also on the noise power spectral density (PSD) they can even account for changing detector characteristics. However, training such networks requires knowing in advance the distribution of PSDs expected to be observed, and therefore can only take place once all data to be analyzed have been gathered. Here, we develop a probabilistic model to forecast future PSDs, greatly increasing the temporal scope of DINGO networks. Using PSDs from the second LIGO-Virgo observing run (O2) $\unicode{x2013}$ plus just a single PSD from the beginning of the third (O3) $\unicode{x2013}$ we show that we can train a DINGO network to perform accurate inference throughout O3 (on 37 real events). We therefore expect this approach to be a key component to enable the use of deep learning techniques for low-latency analyses of gravitational waves.

Neural Importance Sampling for Rapid and Reliable Gravitational-Wave Inference

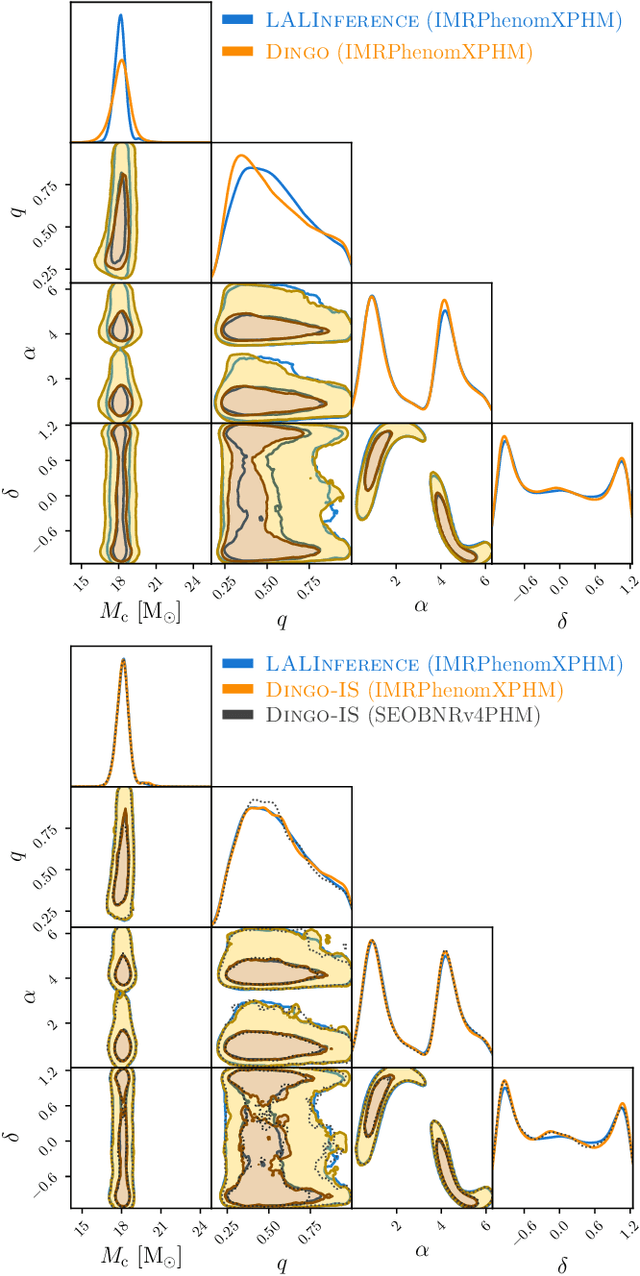
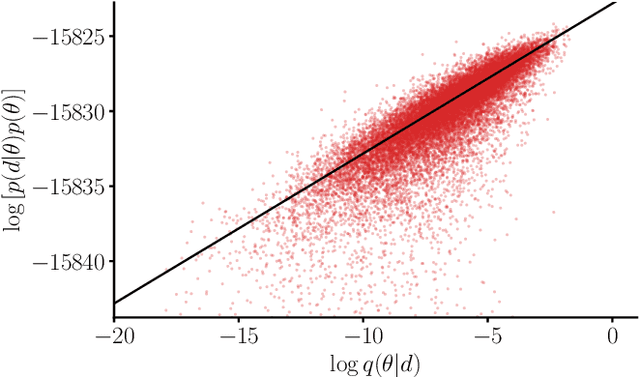
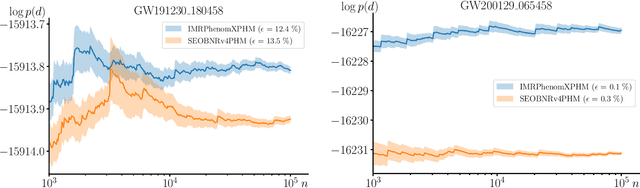
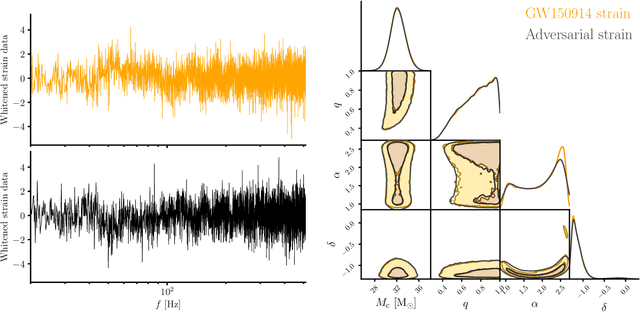
We combine amortized neural posterior estimation with importance sampling for fast and accurate gravitational-wave inference. We first generate a rapid proposal for the Bayesian posterior using neural networks, and then attach importance weights based on the underlying likelihood and prior. This provides (1) a corrected posterior free from network inaccuracies, (2) a performance diagnostic (the sample efficiency) for assessing the proposal and identifying failure cases, and (3) an unbiased estimate of the Bayesian evidence. By establishing this independent verification and correction mechanism we address some of the most frequent criticisms against deep learning for scientific inference. We carry out a large study analyzing 42 binary black hole mergers observed by LIGO and Virgo with the SEOBNRv4PHM and IMRPhenomXPHM waveform models. This shows a median sample efficiency of $\approx 10\%$ (two orders-of-magnitude better than standard samplers) as well as a ten-fold reduction in the statistical uncertainty in the log evidence. Given these advantages, we expect a significant impact on gravitational-wave inference, and for this approach to serve as a paradigm for harnessing deep learning methods in scientific applications.

Group equivariant neural posterior estimation

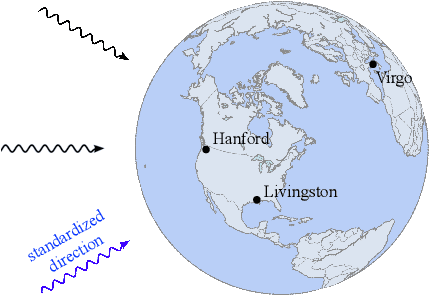
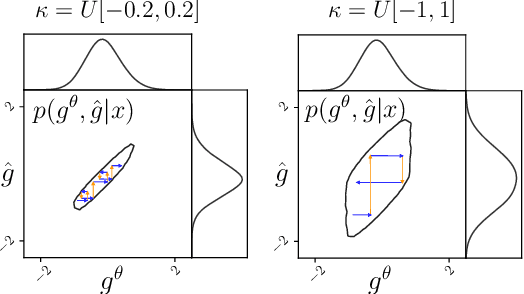
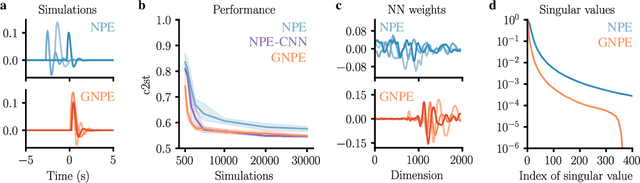
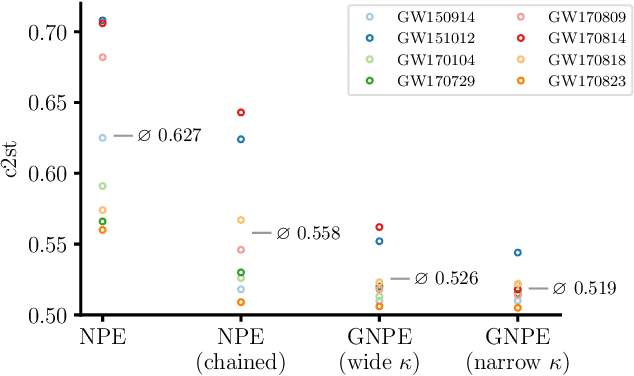
Simulation-based inference with conditional neural density estimators is a powerful approach to solving inverse problems in science. However, these methods typically treat the underlying forward model as a black box, with no way to exploit geometric properties such as equivariances. Equivariances are common in scientific models, however integrating them directly into expressive inference networks (such as normalizing flows) is not straightforward. We here describe an alternative method to incorporate equivariances under joint transformations of parameters and data. Our method -- called group equivariant neural posterior estimation (GNPE) -- is based on self-consistently standardizing the "pose" of the data while estimating the posterior over parameters. It is architecture-independent, and applies both to exact and approximate equivariances. As a real-world application, we use GNPE for amortized inference of astrophysical binary black hole systems from gravitational-wave observations. We show that GNPE achieves state-of-the-art accuracy while reducing inference times by three orders of magnitude.

Real-time gravitational-wave science with neural posterior estimation

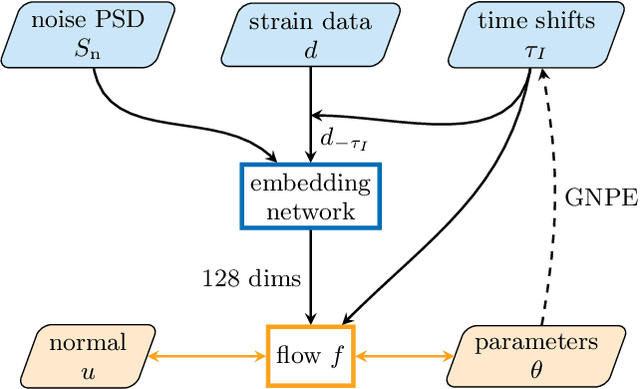
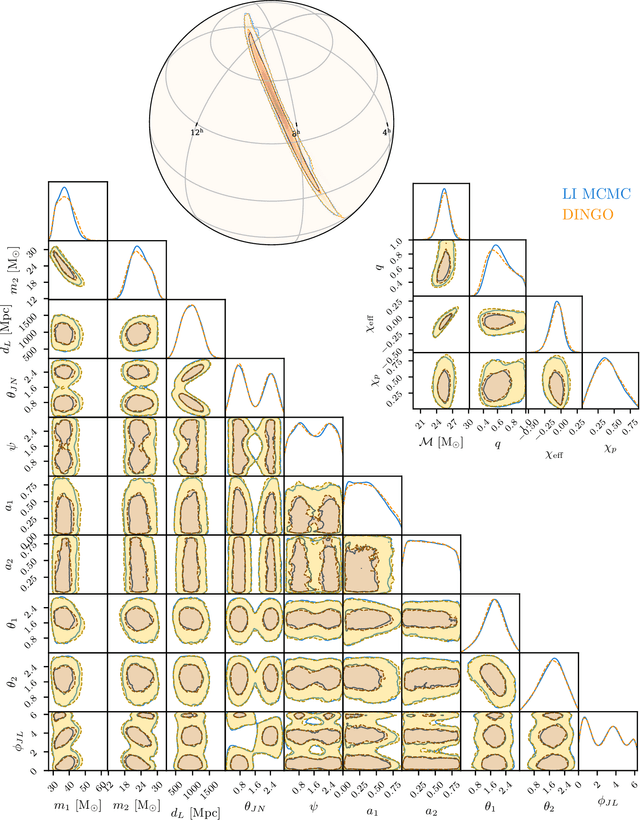
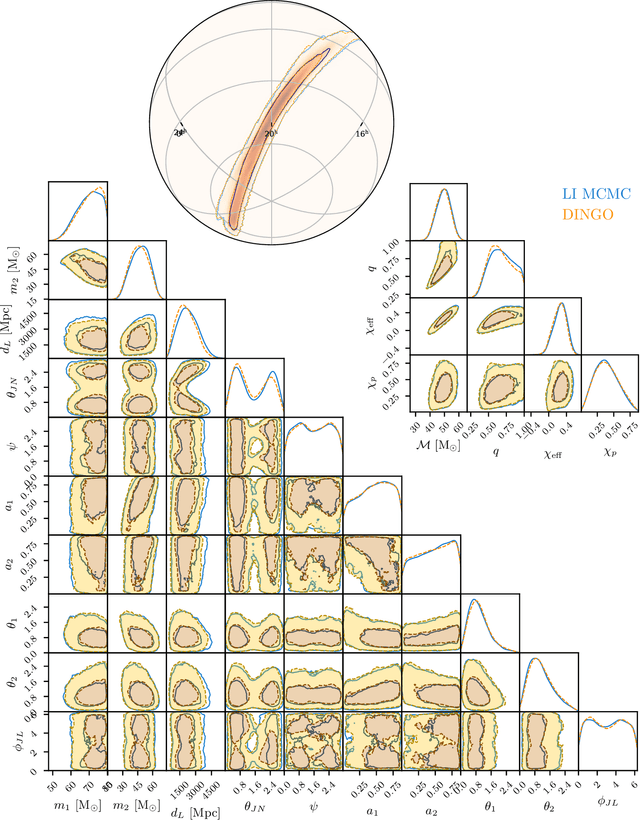
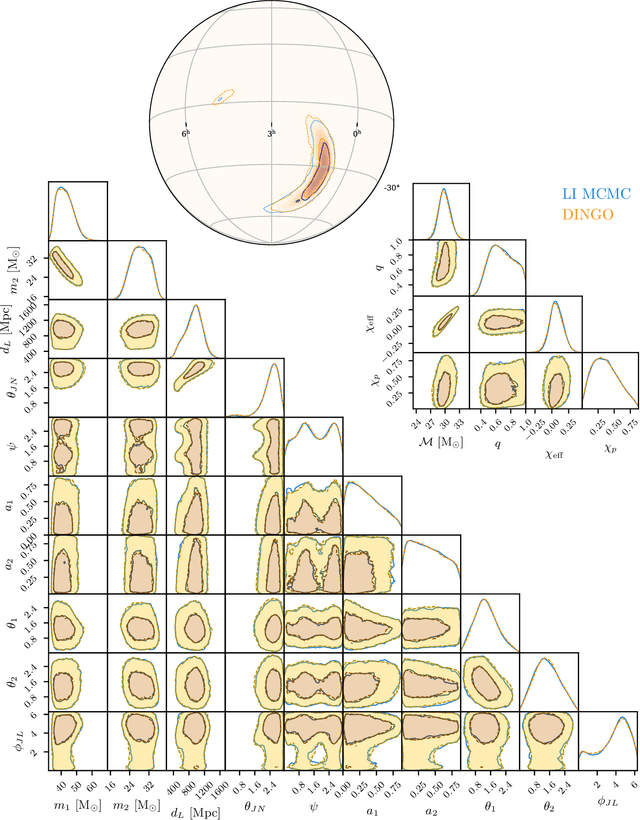
We demonstrate unprecedented accuracy for rapid gravitational-wave parameter estimation with deep learning. Using neural networks as surrogates for Bayesian posterior distributions, we analyze eight gravitational-wave events from the first LIGO-Virgo Gravitational-Wave Transient Catalog and find very close quantitative agreement with standard inference codes, but with inference times reduced from O(day) to a minute per event. Our networks are trained using simulated data, including an estimate of the detector-noise characteristics near the event. This encodes the signal and noise models within millions of neural-network parameters, and enables inference for any observed data consistent with the training distribution, accounting for noise nonstationarity from event to event. Our algorithm -- called "DINGO" -- sets a new standard in fast-and-accurate inference of physical parameters of detected gravitational-wave events, which should enable real-time data analysis without sacrificing accuracy.

Complete parameter inference for GW150914 using deep learning

The LIGO and Virgo gravitational-wave observatories have detected many exciting events over the past five years. As the rate of detections grows with detector sensitivity, this poses a growing computational challenge for data analysis. With this in mind, in this work we apply deep learning techniques to perform fast likelihood-free Bayesian inference for gravitational waves. We train a neural-network conditional density estimator to model posterior probability distributions over the full 15-dimensional space of binary black hole system parameters, given detector strain data from multiple detectors. We use the method of normalizing flows---specifically, a neural spline normalizing flow---which allows for rapid sampling and density estimation. Training the network is likelihood-free, requiring samples from the data generative process, but no likelihood evaluations. Through training, the network learns a global set of posteriors: it can generate thousands of independent posterior samples per second for any strain data consistent with the prior and detector noise characteristics used for training. By training with the detector noise power spectral density estimated at the time of GW150914, and conditioning on the event strain data, we use the neural network to generate accurate posterior samples consistent with analyses using conventional sampling techniques.

Gravitational-wave parameter estimation with autoregressive neural network flows

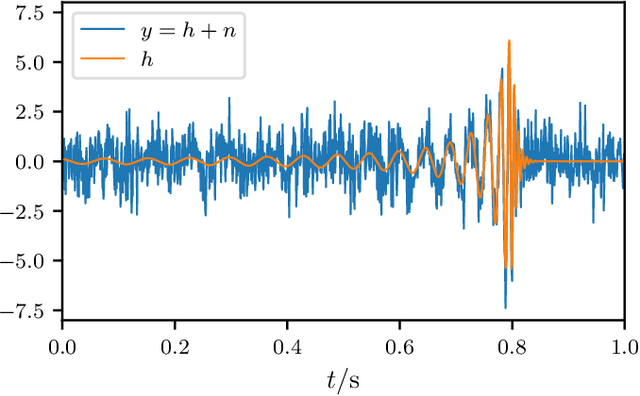
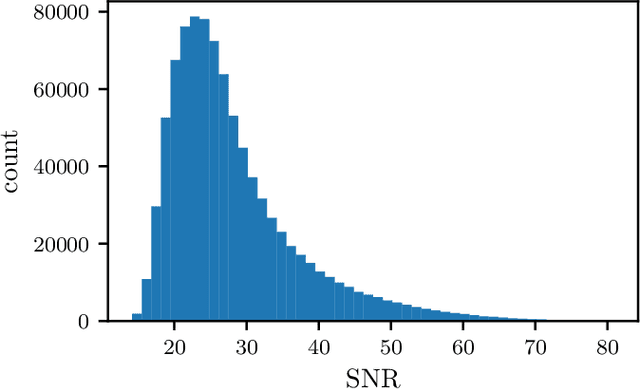
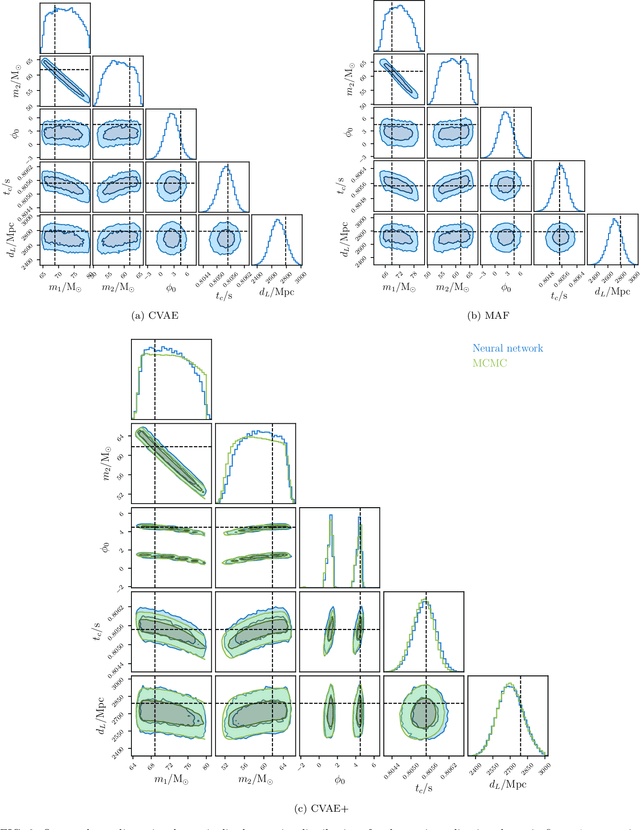
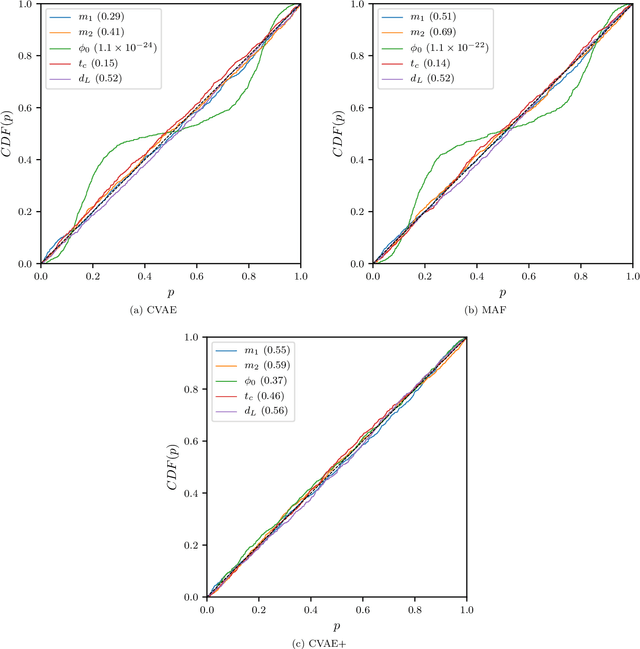
We introduce the use of autoregressive normalizing flows for rapid likelihood-free inference of binary black hole system parameters from gravitational-wave data with deep neural networks. A normalizing flow is an invertible mapping on a sample space that can be used to induce a transformation from a simple probability distribution to a more complex one: if the simple distribution can be rapidly sampled and its density evaluated, then so can the complex distribution. Our first application to gravitational waves uses an autoregressive flow, conditioned on detector strain data, to map a multivariate standard normal distribution into the posterior distribution over system parameters. We train the model on artificial strain data consisting of IMRPhenomPv2 waveforms drawn from a five-parameter $(m_1, m_2, \phi_0, t_c, d_L)$ prior and stationary Gaussian noise realizations with a fixed power spectral density. This gives performance comparable to current best deep-learning approaches to gravitational-wave parameter estimation. We then build a more powerful latent variable model by incorporating autoregressive flows within the variational autoencoder framework. This model has performance comparable to Markov chain Monte Carlo and, in particular, successfully models the multimodal $\phi_0$ posterior. Finally, we train the autoregressive latent variable model on an expanded parameter space, including also aligned spins $(\chi_{1z}, \chi_{2z})$ and binary inclination $\theta_{JN}$, and show that all parameters and degeneracies are well-recovered. In all cases, sampling is extremely fast, requiring less than two seconds to draw $10^4$ posterior samples.