Flow Matching for Atmospheric Retrieval of Exoplanets: Where Reliability meets Adaptive Noise Levels

Inferring atmospheric properties of exoplanets from observed spectra is key to understanding their formation, evolution, and habitability. Since traditional Bayesian approaches to atmospheric retrieval (e.g., nested sampling) are computationally expensive, a growing number of machine learning (ML) methods such as neural posterior estimation (NPE) have been proposed. We seek to make ML-based atmospheric retrieval (1) more reliable and accurate with verified results, and (2) more flexible with respect to the underlying neural networks and the choice of the assumed noise models. First, we adopt flow matching posterior estimation (FMPE) as a new ML approach to atmospheric retrieval. FMPE maintains many advantages of NPE, but provides greater architectural flexibility and scalability. Second, we use importance sampling (IS) to verify and correct ML results, and to compute an estimate of the Bayesian evidence. Third, we condition our ML models on the assumed noise level of a spectrum (i.e., error bars), thus making them adaptable to different noise models. Both our noise level-conditional FMPE and NPE models perform on par with nested sampling across a range of noise levels when tested on simulated data. FMPE trains about 3 times faster than NPE and yields higher IS efficiencies. IS successfully corrects inaccurate ML results, identifies model failures via low efficiencies, and provides accurate estimates of the Bayesian evidence. FMPE is a powerful alternative to NPE for fast, amortized, and parallelizable atmospheric retrieval. IS can verify results, thus helping to build confidence in ML-based approaches, while also facilitating model comparison via the evidence ratio. Noise level conditioning allows design studies for future instruments to be scaled up, for example, in terms of the range of signal-to-noise ratios.

Real-time gravitational-wave inference for binary neutron stars using machine learning

Mergers of binary neutron stars (BNSs) emit signals in both the gravitational-wave (GW) and electromagnetic (EM) spectra. Famously, the 2017 multi-messenger observation of GW170817 led to scientific discoveries across cosmology, nuclear physics, and gravity. Central to these results were the sky localization and distance obtained from GW data, which, in the case of GW170817, helped to identify the associated EM transient, AT 2017gfo, 11 hours after the GW signal. Fast analysis of GW data is critical for directing time-sensitive EM observations; however, due to challenges arising from the length and complexity of signals, it is often necessary to make approximations that sacrifice accuracy. Here, we develop a machine learning approach that performs complete BNS inference in just one second without making any such approximations. This is enabled by a new method for explicit integration of physical domain knowledge into neural networks. Our approach enhances multi-messenger observations by providing (i) accurate localization even before the merger; (ii) improved localization precision by $\sim30\%$ compared to approximate low-latency methods; and (iii) detailed information on luminosity distance, inclination, and masses, which can be used to prioritize expensive telescope time. Additionally, the flexibility and reduced cost of our method open new opportunities for equation-of-state and waveform systematics studies. Finally, we demonstrate that our method scales to extremely long signals, up to an hour in length, thus serving as a blueprint for data analysis for next-generation ground- and space-based detectors.

Inferring Atmospheric Properties of Exoplanets with Flow Matching and Neural Importance Sampling

Atmospheric retrievals (AR) characterize exoplanets by estimating atmospheric parameters from observed light spectra, typically by framing the task as a Bayesian inference problem. However, traditional approaches such as nested sampling are computationally expensive, thus sparking an interest in solutions based on machine learning (ML). In this ongoing work, we first explore flow matching posterior estimation (FMPE) as a new ML-based method for AR and find that, in our case, it is more accurate than neural posterior estimation (NPE), but less accurate than nested sampling. We then combine both FMPE and NPE with importance sampling, in which case both methods outperform nested sampling in terms of accuracy and simulation efficiency. Going forward, our analysis suggests that simulation-based inference with likelihood-based importance sampling provides a framework for accurate and efficient AR that may become a valuable tool not only for the analysis of observational data from existing telescopes, but also for the development of new missions and instruments.

Flow Matching for Scalable Simulation-Based Inference

Neural posterior estimation methods based on discrete normalizing flows have become established tools for simulation-based inference (SBI), but scaling them to high-dimensional problems can be challenging. Building on recent advances in generative modeling, we here present flow matching posterior estimation (FMPE), a technique for SBI using continuous normalizing flows. Like diffusion models, and in contrast to discrete flows, flow matching allows for unconstrained architectures, providing enhanced flexibility for complex data modalities. Flow matching, therefore, enables exact density evaluation, fast training, and seamless scalability to large architectures--making it ideal for SBI. We show that FMPE achieves competitive performance on an established SBI benchmark, and then demonstrate its improved scalability on a challenging scientific problem: for gravitational-wave inference, FMPE outperforms methods based on comparable discrete flows, reducing training time by 30% with substantially improved accuracy. Our work underscores the potential of FMPE to enhance performance in challenging inference scenarios, thereby paving the way for more advanced applications to scientific problems.

Out-of-Variable Generalization

The ability of an agent to perform well in new and unseen environments is a crucial aspect of intelligence. In machine learning, this ability is referred to as strong or out-of-distribution generalization. However, simply considering differences in data distributions is not sufficient to fully capture differences in environments. In the present paper, we assay out-of-variable generalization, which refers to an agent's ability to handle new situations that involve variables never jointly observed before. We expect that such ability is important also for AI-driven scientific discovery: humans, too, explore 'Nature' by probing, observing and measuring subsets of variables at one time. Mathematically, it requires efficient re-use of past marginal knowledge, i.e., knowledge over subsets of variables. We study this problem, focusing on prediction tasks that involve observing overlapping, yet distinct, sets of causal parents. We show that the residual distribution of one environment encodes the partial derivative of the true generating function with respect to the unobserved causal parent. Hence, learning from the residual allows zero-shot prediction even when we never observe the outcome variable in the other environment.

On the Interventional Kullback-Leibler Divergence

Modern machine learning approaches excel in static settings where a large amount of i.i.d. training data are available for a given task. In a dynamic environment, though, an intelligent agent needs to be able to transfer knowledge and re-use learned components across domains. It has been argued that this may be possible through causal models, aiming to mirror the modularity of the real world in terms of independent causal mechanisms. However, the true causal structure underlying a given set of data is generally not identifiable, so it is desirable to have means to quantify differences between models (e.g., between the ground truth and an estimate), on both the observational and interventional level. In the present work, we introduce the Interventional Kullback-Leibler (IKL) divergence to quantify both structural and distributional differences between models based on a finite set of multi-environment distributions generated by interventions from the ground truth. Since we generally cannot quantify all differences between causal models for every finite set of interventional distributions, we propose a sufficient condition on the intervention targets to identify subsets of observed variables on which the models provably agree or disagree.

Adapting to noise distribution shifts in flow-based gravitational-wave inference

Deep learning techniques for gravitational-wave parameter estimation have emerged as a fast alternative to standard samplers $\unicode{x2013}$ producing results of comparable accuracy. These approaches (e.g., DINGO) enable amortized inference by training a normalizing flow to represent the Bayesian posterior conditional on observed data. By conditioning also on the noise power spectral density (PSD) they can even account for changing detector characteristics. However, training such networks requires knowing in advance the distribution of PSDs expected to be observed, and therefore can only take place once all data to be analyzed have been gathered. Here, we develop a probabilistic model to forecast future PSDs, greatly increasing the temporal scope of DINGO networks. Using PSDs from the second LIGO-Virgo observing run (O2) $\unicode{x2013}$ plus just a single PSD from the beginning of the third (O3) $\unicode{x2013}$ we show that we can train a DINGO network to perform accurate inference throughout O3 (on 37 real events). We therefore expect this approach to be a key component to enable the use of deep learning techniques for low-latency analyses of gravitational waves.

Neural Importance Sampling for Rapid and Reliable Gravitational-Wave Inference

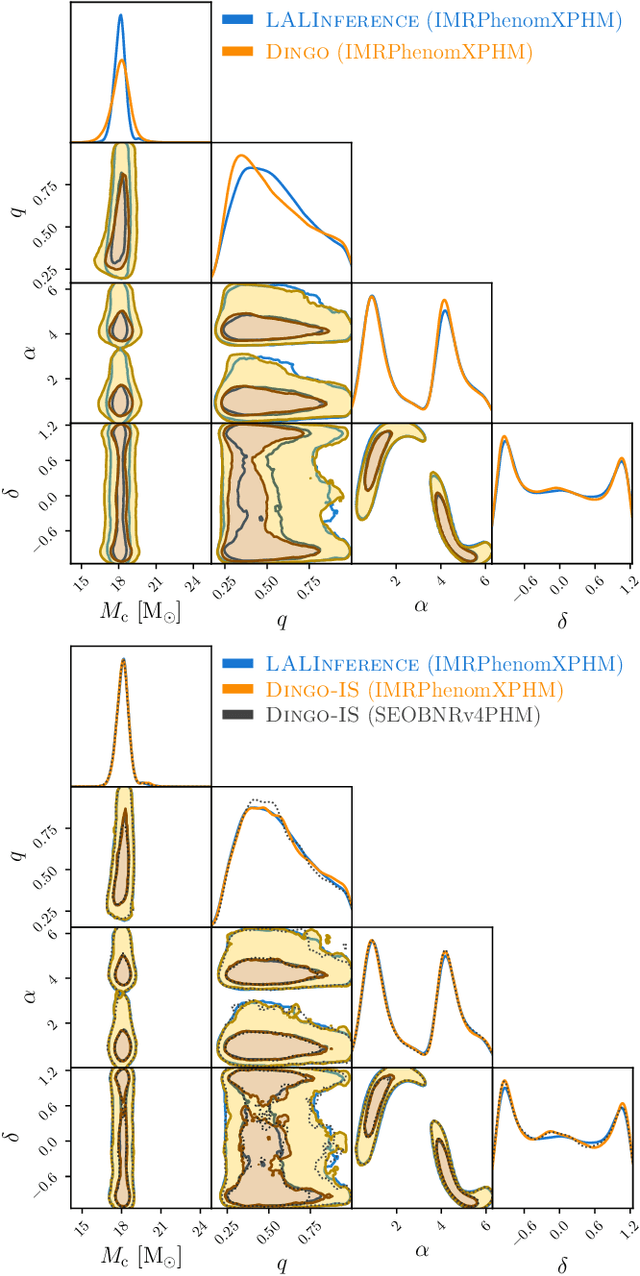
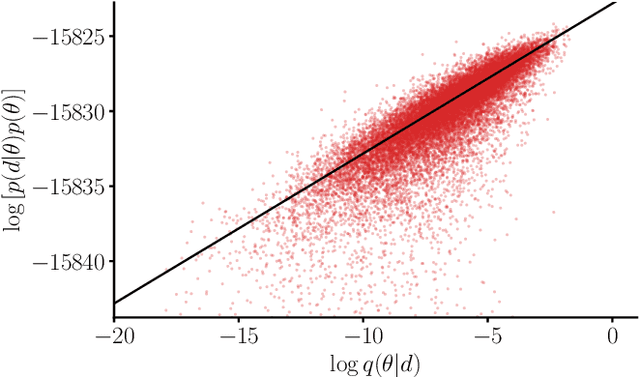
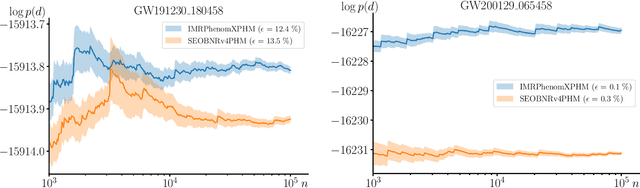
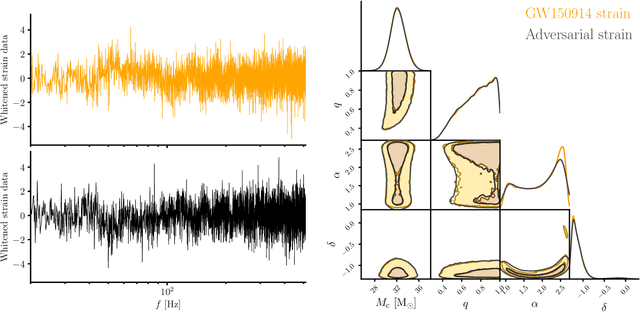
We combine amortized neural posterior estimation with importance sampling for fast and accurate gravitational-wave inference. We first generate a rapid proposal for the Bayesian posterior using neural networks, and then attach importance weights based on the underlying likelihood and prior. This provides (1) a corrected posterior free from network inaccuracies, (2) a performance diagnostic (the sample efficiency) for assessing the proposal and identifying failure cases, and (3) an unbiased estimate of the Bayesian evidence. By establishing this independent verification and correction mechanism we address some of the most frequent criticisms against deep learning for scientific inference. We carry out a large study analyzing 42 binary black hole mergers observed by LIGO and Virgo with the SEOBNRv4PHM and IMRPhenomXPHM waveform models. This shows a median sample efficiency of $\approx 10\%$ (two orders-of-magnitude better than standard samplers) as well as a ten-fold reduction in the statistical uncertainty in the log evidence. Given these advantages, we expect a significant impact on gravitational-wave inference, and for this approach to serve as a paradigm for harnessing deep learning methods in scientific applications.

Beta-VAE Reproducibility: Challenges and Extensions

$\beta$-VAE is a follow-up technique to variational autoencoders that proposes special weighting of the KL divergence term in the VAE loss to obtain disentangled representations. Unsupervised learning is known to be brittle even on toy datasets and a meaningful, mathematically precise definition of disentanglement remains difficult to find. Here we investigate the original $\beta$-VAE paper and add evidence to the results previously obtained indicating its lack of reproducibility. We also further expand the experimentation of the models and include further more complex datasets in the analysis. We also implement an FID scoring metric for the $\beta$-VAE model and conclude a qualitative analysis of the results obtained. We end with a brief discussion on possible future investigations that can be conducted to add more robustness to the claims.