Apertus: Democratizing Open and Compliant LLMs for Global Language Environments

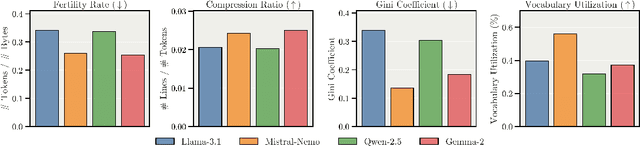
We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.

Adaptable Cardiovascular Disease Risk Prediction from Heterogeneous Data using Large Language Models

Cardiovascular disease (CVD) risk prediction models are essential for identifying high-risk individuals and guiding preventive actions. However, existing models struggle with the challenges of real-world clinical practice as they oversimplify patient profiles, rely on rigid input schemas, and are sensitive to distribution shifts. We developed AdaCVD, an adaptable CVD risk prediction framework built on large language models extensively fine-tuned on over half a million participants from the UK Biobank. In benchmark comparisons, AdaCVD surpasses established risk scores and standard machine learning approaches, achieving state-of-the-art performance. Crucially, for the first time, it addresses key clinical challenges across three dimensions: it flexibly incorporates comprehensive yet variable patient information; it seamlessly integrates both structured data and unstructured text; and it rapidly adapts to new patient populations using minimal additional data. In stratified analyses, it demonstrates robust performance across demographic, socioeconomic, and clinical subgroups, including underrepresented cohorts. AdaCVD offers a promising path toward more flexible, AI-driven clinical decision support tools suited to the realities of heterogeneous and dynamic healthcare environments.

Neural Unbalanced Optimal Transport via Cycle-Consistent Semi-Couplings

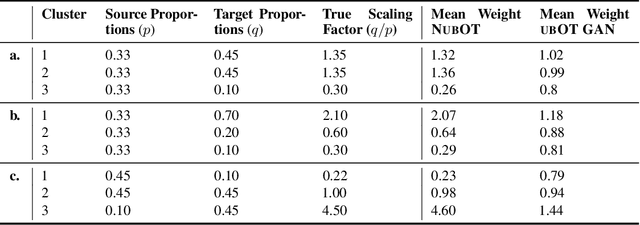
Comparing unpaired samples of a distribution or population taken at different points in time is a fundamental task in many application domains where measuring populations is destructive and cannot be done repeatedly on the same sample, such as in single-cell biology. Optimal transport (OT) can solve this challenge by learning an optimal coupling of samples across distributions from unpaired data. However, the usual formulation of OT assumes conservation of mass, which is violated in unbalanced scenarios in which the population size changes (e.g., cell proliferation or death) between measurements. In this work, we introduce NubOT, a neural unbalanced OT formulation that relies on the formalism of semi-couplings to account for creation and destruction of mass. To estimate such semi-couplings and generalize out-of-sample, we derive an efficient parameterization based on neural optimal transport maps and propose a novel algorithmic scheme through a cycle-consistent training procedure. We apply our method to the challenging task of forecasting heterogeneous responses of multiple cancer cell lines to various drugs, where we observe that by accurately modeling cell proliferation and death, our method yields notable improvements over previous neural optimal transport methods.