AI-powered virtual tissues from spatial proteomics for clinical diagnostics and biomedical discovery

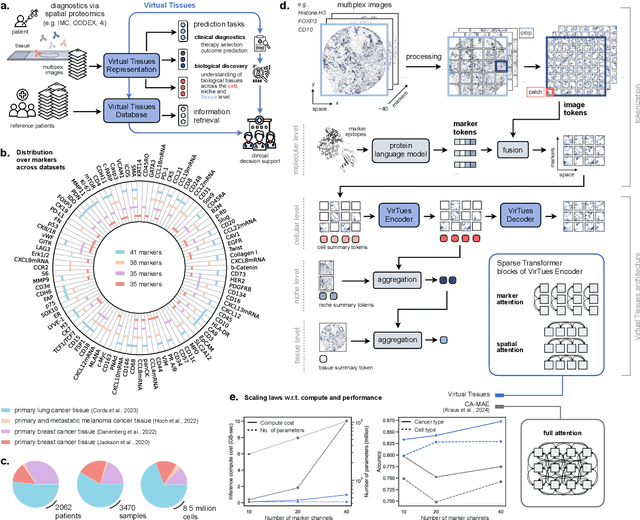
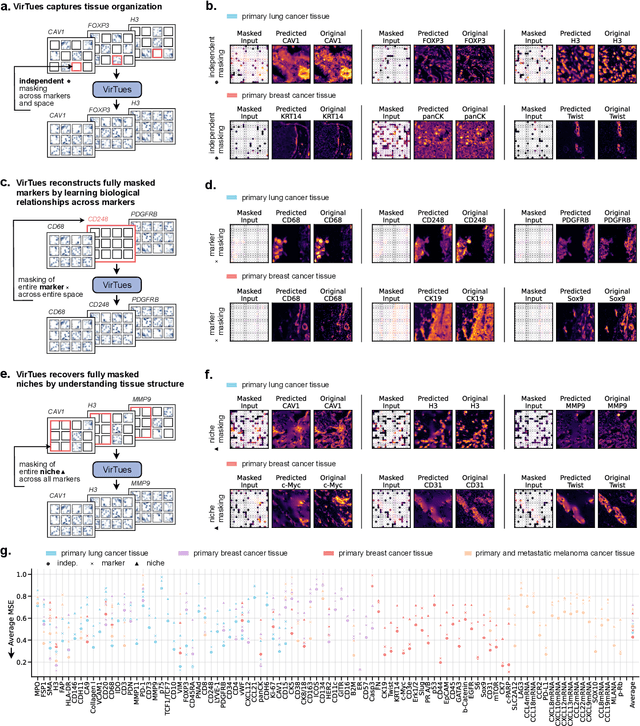
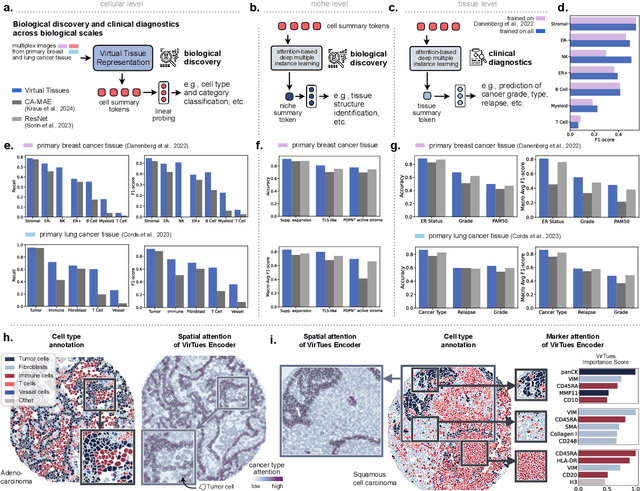
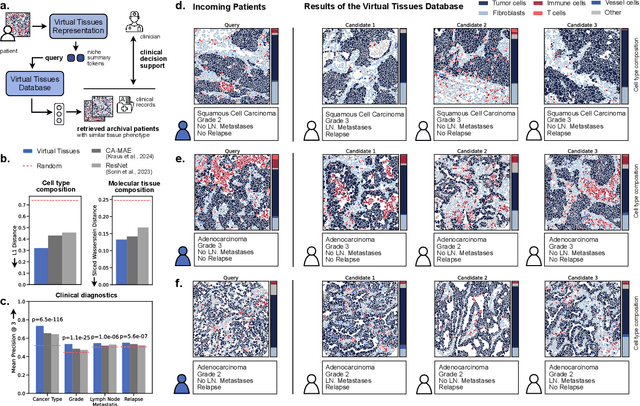
Spatial proteomics technologies have transformed our understanding of complex tissue architectures by enabling simultaneous analysis of multiple molecular markers and their spatial organization. The high dimensionality of these data, varying marker combinations across experiments and heterogeneous study designs pose unique challenges for computational analysis. Here, we present Virtual Tissues (VirTues), a foundation model framework for biological tissues that operates across the molecular, cellular and tissue scale. VirTues introduces innovations in transformer architecture design, including a novel tokenization scheme that captures both spatial and marker dimensions, and attention mechanisms that scale to high-dimensional multiplex data while maintaining interpretability. Trained on diverse cancer and non-cancer tissue datasets, VirTues demonstrates strong generalization capabilities without task-specific fine-tuning, enabling cross-study analysis and novel marker integration. As a generalist model, VirTues outperforms existing approaches across clinical diagnostics, biological discovery and patient case retrieval tasks, while providing insights into tissue function and disease mechanisms.

How to Build the Virtual Cell with Artificial Intelligence: Priorities and Opportunities

The cell is arguably the smallest unit of life and is central to understanding biology. Accurate modeling of cells is important for this understanding as well as for determining the root causes of disease. Recent advances in artificial intelligence (AI), combined with the ability to generate large-scale experimental data, present novel opportunities to model cells. Here we propose a vision of AI-powered Virtual Cells, where robust representations of cells and cellular systems under different conditions are directly learned from growing biological data across measurements and scales. We discuss desired capabilities of AI Virtual Cells, including generating universal representations of biological entities across scales, and facilitating interpretable in silico experiments to predict and understand their behavior using Virtual Instruments. We further address the challenges, opportunities and requirements to realize this vision including data needs, evaluation strategies, and community standards and engagement to ensure biological accuracy and broad utility. We envision a future where AI Virtual Cells help identify new drug targets, predict cellular responses to perturbations, as well as scale hypothesis exploration. With open science collaborations across the biomedical ecosystem that includes academia, philanthropy, and the biopharma and AI industries, a comprehensive predictive understanding of cell mechanisms and interactions is within reach.

EquiReact: An equivariant neural network for chemical reactions

Equivariant neural networks have considerably improved the accuracy and data-efficiency of predictions of molecular properties. Building on this success, we introduce EquiReact, an equivariant neural network to infer properties of chemical reactions, built from three-dimensional structures of reactants and products. We illustrate its competitive performance on the prediction of activation barriers on the GDB7-22-TS, Cyclo-23-TS and Proparg-21-TS datasets with different regimes according to the inclusion of atom-mapping information. We show that, compared to state-of-the-art models for reaction property prediction, EquiReact offers: (i) a flexible model with reduced sensitivity between atom-mapping regimes, (ii) better extrapolation capabilities to unseen chemistries, (iii) impressive prediction errors for datasets exhibiting subtle variations in three-dimensional geometries of reactants/products, (iv) reduced sensitivity to geometry quality and (iv) excellent data efficiency.

Transition Path Sampling with Boltzmann Generator-based MCMC Moves

Sampling all possible transition paths between two 3D states of a molecular system has various applications ranging from catalyst design to drug discovery. Current approaches to sample transition paths use Markov chain Monte Carlo and rely on time-intensive molecular dynamics simulations to find new paths. Our approach operates in the latent space of a normalizing flow that maps from the molecule's Boltzmann distribution to a Gaussian, where we propose new paths without requiring molecular simulations. Using alanine dipeptide, we explore Metropolis-Hastings acceptance criteria in the latent space for exact sampling and investigate different latent proposal mechanisms.

Unbalanced Diffusion Schrödinger Bridge

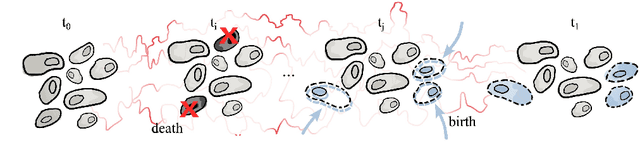
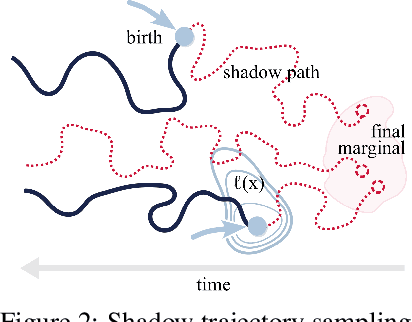
Schr\"odinger bridges (SBs) provide an elegant framework for modeling the temporal evolution of populations in physical, chemical, or biological systems. Such natural processes are commonly subject to changes in population size over time due to the emergence of new species or birth and death events. However, existing neural parameterizations of SBs such as diffusion Schr\"odinger bridges (DSBs) are restricted to settings in which the endpoints of the stochastic process are both probability measures and assume conservation of mass constraints. To address this limitation, we introduce unbalanced DSBs which model the temporal evolution of marginals with arbitrary finite mass. This is achieved by deriving the time reversal of stochastic differential equations with killing and birth terms. We present two novel algorithmic schemes that comprise a scalable objective function for training unbalanced DSBs and provide a theoretical analysis alongside challenging applications on predicting heterogeneous molecular single-cell responses to various cancer drugs and simulating the emergence and spread of new viral variants.

Aligned Diffusion Schrödinger Bridges

Diffusion Schr\"odinger bridges (DSB) have recently emerged as a powerful framework for recovering stochastic dynamics via their marginal observations at different time points. Despite numerous successful applications, existing algorithms for solving DSBs have so far failed to utilize the structure of aligned data, which naturally arises in many biological phenomena. In this paper, we propose a novel algorithmic framework that, for the first time, solves DSBs while respecting the data alignment. Our approach hinges on a combination of two decades-old ideas: The classical Schr\"odinger bridge theory and Doob's $h$-transform. Compared to prior methods, our approach leads to a simpler training procedure with lower variance, which we further augment with principled regularization schemes. This ultimately leads to sizeable improvements across experiments on synthetic and real data, including the tasks of rigid protein docking and temporal evolution of cellular differentiation processes.

Neural Unbalanced Optimal Transport via Cycle-Consistent Semi-Couplings

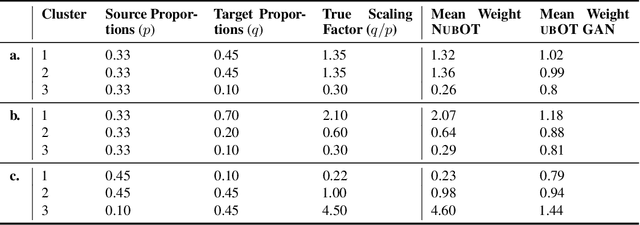
Comparing unpaired samples of a distribution or population taken at different points in time is a fundamental task in many application domains where measuring populations is destructive and cannot be done repeatedly on the same sample, such as in single-cell biology. Optimal transport (OT) can solve this challenge by learning an optimal coupling of samples across distributions from unpaired data. However, the usual formulation of OT assumes conservation of mass, which is violated in unbalanced scenarios in which the population size changes (e.g., cell proliferation or death) between measurements. In this work, we introduce NubOT, a neural unbalanced OT formulation that relies on the formalism of semi-couplings to account for creation and destruction of mass. To estimate such semi-couplings and generalize out-of-sample, we derive an efficient parameterization based on neural optimal transport maps and propose a novel algorithmic scheme through a cycle-consistent training procedure. We apply our method to the challenging task of forecasting heterogeneous responses of multiple cancer cell lines to various drugs, where we observe that by accurately modeling cell proliferation and death, our method yields notable improvements over previous neural optimal transport methods.

Supervised Training of Conditional Monge Maps

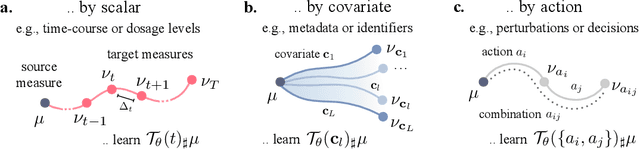
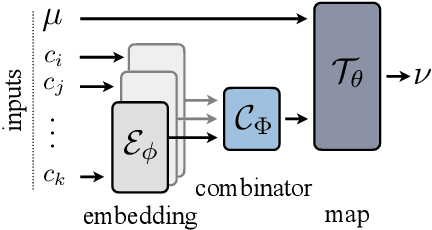
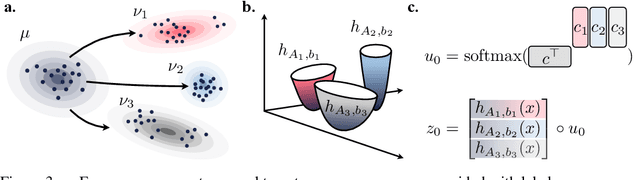
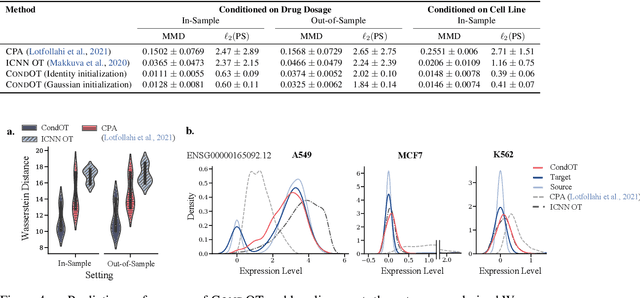
Optimal transport (OT) theory describes general principles to define and select, among many possible choices, the most efficient way to map a probability measure onto another. That theory has been mostly used to estimate, given a pair of source and target probability measures $(\mu,\nu)$, a parameterized map $T_\theta$ that can efficiently map $\mu$ onto $\nu$. In many applications, such as predicting cell responses to treatments, the data measures $\mu,\nu$ (features of untreated/treated cells) that define optimal transport problems do not arise in isolation but are associated with a context $c$ (the treatment). To account for and incorporate that context in OT estimation, we introduce CondOT, an approach to estimate OT maps conditioned on a context variable, using several pairs of measures $(\mu_i, \nu_i)$ tagged with a context label $c_i$. Our goal is to % extract from a dataset of labeled pairs $\{(c_i, (\mu_i, \nu_i))\}$ learn a global map $\mathcal{T}_{\theta}$ which is not only expected to fit em all pairs in the dataset $\{(c_i, (\mu_i, \nu_i))\}$, i.e., $\mathcal{T}_{\theta}(c_i) \sharp\mu_i \approx \nu_i$, but should generalize to produce meaningful maps $\mathcal{T}_{\theta}(c_{\text{new}})$ conditioned on unseen contexts $c_{\text{new}}$. Our approach harnesses and provides a novel usage for partially input convex neural networks, for which we introduce a robust and efficient initialization strategy inspired by Gaussian approximations. We demonstrate the ability of CondOT to infer the effect of an arbitrary combination of genetic or therapeutic perturbations on single cells, using only observations of the effects of said perturbations separately.

Invariant Causal Mechanisms through Distribution Matching

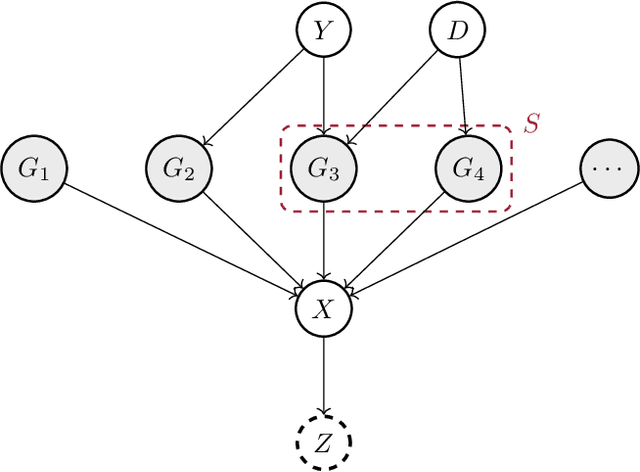
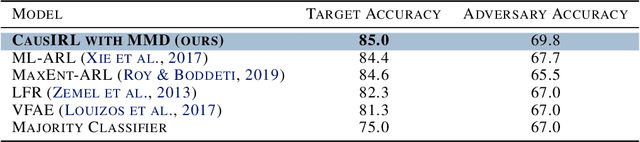
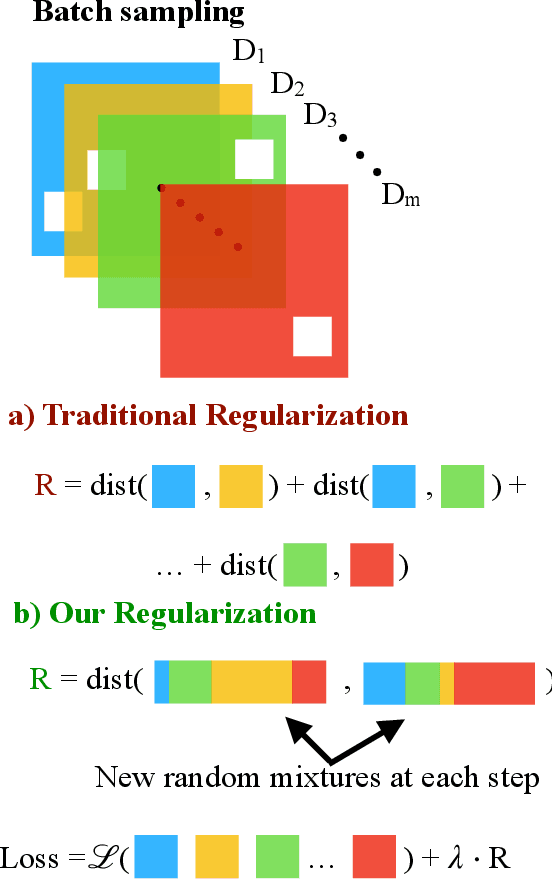
Learning representations that capture the underlying data generating process is a key problem for data efficient and robust use of neural networks. One key property for robustness which the learned representation should capture and which recently received a lot of attention is described by the notion of invariance. In this work we provide a causal perspective and new algorithm for learning invariant representations. Empirically we show that this algorithm works well on a diverse set of tasks and in particular we observe state-of-the-art performance on domain generalization, where we are able to significantly boost the score of existing models.

Multi-Scale Representation Learning on Proteins

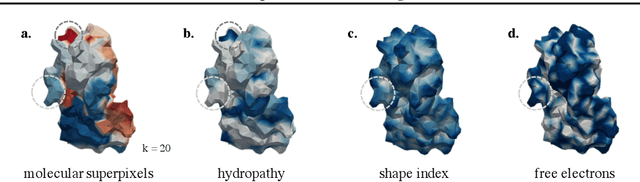
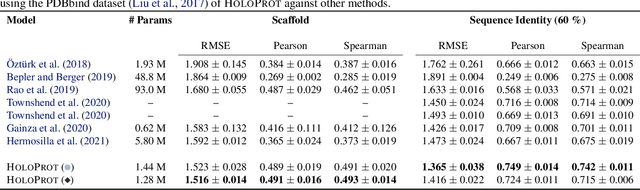
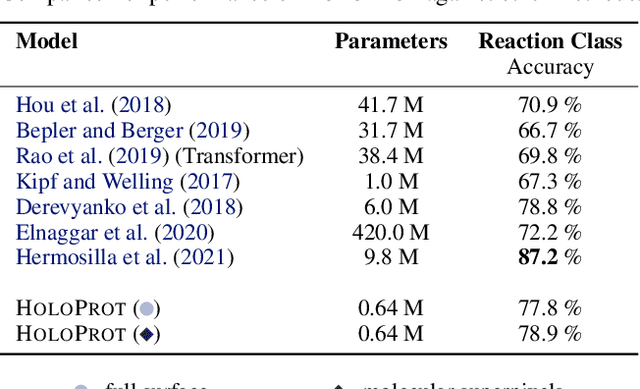
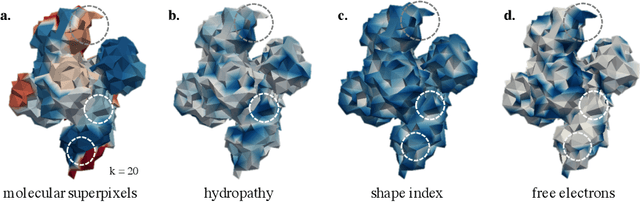
Proteins are fundamental biological entities mediating key roles in cellular function and disease. This paper introduces a multi-scale graph construction of a protein -- HoloProt -- connecting surface to structure and sequence. The surface captures coarser details of the protein, while sequence as primary component and structure -- comprising secondary and tertiary components -- capture finer details. Our graph encoder then learns a multi-scale representation by allowing each level to integrate the encoding from level(s) below with the graph at that level. We test the learned representation on different tasks, (i.) ligand binding affinity (regression), and (ii.) protein function prediction (classification). On the regression task, contrary to previous methods, our model performs consistently and reliably across different dataset splits, outperforming all baselines on most splits. On the classification task, it achieves a performance close to the top-performing model while using 10x fewer parameters. To improve the memory efficiency of our construction, we segment the multiplex protein surface manifold into molecular superpixels and substitute the surface with these superpixels at little to no performance loss.