Vignesh Ram Somnath
SynCoGen: Synthesizable 3D Molecule Generation via Joint Reaction and Coordinate Modeling
Jul 16, 2025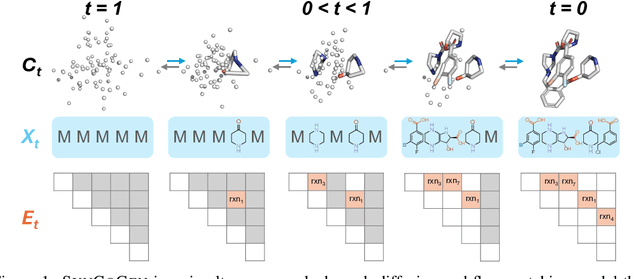
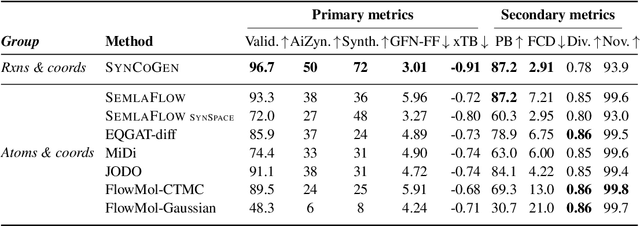
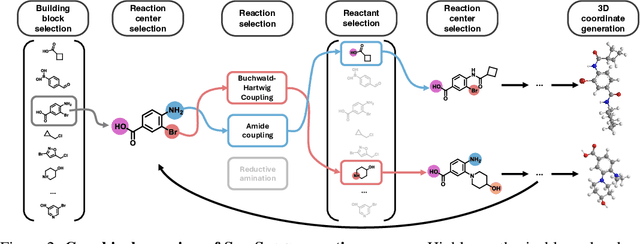
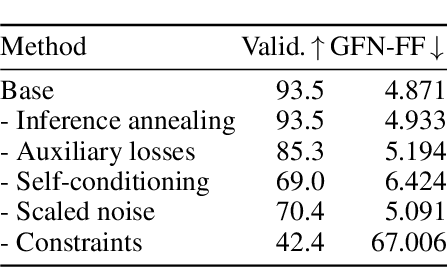
Abstract:Ensuring synthesizability in generative small molecule design remains a major challenge. While recent developments in synthesizable molecule generation have demonstrated promising results, these efforts have been largely confined to 2D molecular graph representations, limiting the ability to perform geometry-based conditional generation. In this work, we present SynCoGen (Synthesizable Co-Generation), a single framework that combines simultaneous masked graph diffusion and flow matching for synthesizable 3D molecule generation. SynCoGen samples from the joint distribution of molecular building blocks, chemical reactions, and atomic coordinates. To train the model, we curated SynSpace, a dataset containing over 600K synthesis-aware building block graphs and 3.3M conformers. SynCoGen achieves state-of-the-art performance in unconditional small molecule graph and conformer generation, and the model delivers competitive performance in zero-shot molecular linker design for protein ligand generation in drug discovery. Overall, this multimodal formulation represents a foundation for future applications enabled by non-autoregressive molecular generation, including analog expansion, lead optimization, and direct structure conditioning.
EquiReact: An equivariant neural network for chemical reactions
Dec 13, 2023Abstract:Equivariant neural networks have considerably improved the accuracy and data-efficiency of predictions of molecular properties. Building on this success, we introduce EquiReact, an equivariant neural network to infer properties of chemical reactions, built from three-dimensional structures of reactants and products. We illustrate its competitive performance on the prediction of activation barriers on the GDB7-22-TS, Cyclo-23-TS and Proparg-21-TS datasets with different regimes according to the inclusion of atom-mapping information. We show that, compared to state-of-the-art models for reaction property prediction, EquiReact offers: (i) a flexible model with reduced sensitivity between atom-mapping regimes, (ii) better extrapolation capabilities to unseen chemistries, (iii) impressive prediction errors for datasets exhibiting subtle variations in three-dimensional geometries of reactants/products, (iv) reduced sensitivity to geometry quality and (iv) excellent data efficiency.
DockGame: Cooperative Games for Multimeric Rigid Protein Docking
Oct 09, 2023Abstract:Protein interactions and assembly formation are fundamental to most biological processes. Predicting the assembly structure from constituent proteins -- referred to as the protein docking task -- is thus a crucial step in protein design applications. Most traditional and deep learning methods for docking have focused mainly on binary docking, following either a search-based, regression-based, or generative modeling paradigm. In this paper, we focus on the less-studied multimeric (i.e., two or more proteins) docking problem. We introduce DockGame, a novel game-theoretic framework for docking -- we view protein docking as a cooperative game between proteins, where the final assembly structure(s) constitute stable equilibria w.r.t. the underlying game potential. Since we do not have access to the true potential, we consider two approaches - i) learning a surrogate game potential guided by physics-based energy functions and computing equilibria by simultaneous gradient updates, and ii) sampling from the Gibbs distribution of the true potential by learning a diffusion generative model over the action spaces (rotations and translations) of all proteins. Empirically, on the Docking Benchmark 5.5 (DB5.5) dataset, DockGame has much faster runtimes than traditional docking methods, can generate multiple plausible assembly structures, and achieves comparable performance to existing binary docking baselines, despite solving the harder task of coordinating multiple protein chains.
Aligned Diffusion Schrödinger Bridges
Feb 22, 2023Abstract:Diffusion Schr\"odinger bridges (DSB) have recently emerged as a powerful framework for recovering stochastic dynamics via their marginal observations at different time points. Despite numerous successful applications, existing algorithms for solving DSBs have so far failed to utilize the structure of aligned data, which naturally arises in many biological phenomena. In this paper, we propose a novel algorithmic framework that, for the first time, solves DSBs while respecting the data alignment. Our approach hinges on a combination of two decades-old ideas: The classical Schr\"odinger bridge theory and Doob's $h$-transform. Compared to prior methods, our approach leads to a simpler training procedure with lower variance, which we further augment with principled regularization schemes. This ultimately leads to sizeable improvements across experiments on synthetic and real data, including the tasks of rigid protein docking and temporal evolution of cellular differentiation processes.
Isotropic Gaussian Processes on Finite Spaces of Graphs
Nov 03, 2022
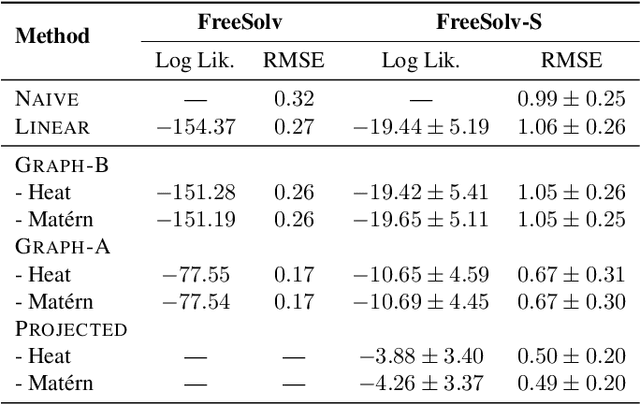
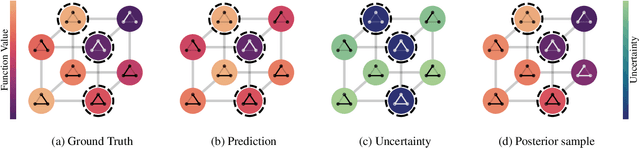
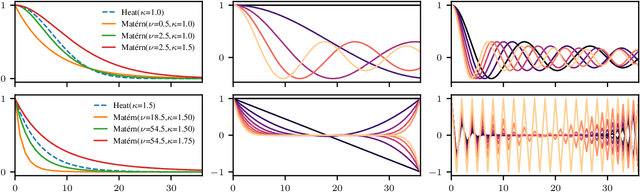
Abstract:We propose a principled way to define Gaussian process priors on various sets of unweighted graphs: directed or undirected, with or without loops. We endow each of these sets with a geometric structure, inducing the notions of closeness and symmetries, by turning them into a vertex set of an appropriate metagraph. Building on this, we describe the class of priors that respect this structure and are analogous to the Euclidean isotropic processes, like squared exponential or Mat\'ern. We propose an efficient computational technique for the ostensibly intractable problem of evaluating these priors' kernels, making such Gaussian processes usable within the usual toolboxes and downstream applications. We go further to consider sets of equivalence classes of unweighted graphs and define the appropriate versions of priors thereon. We prove a hardness result, showing that in this case, exact kernel computation cannot be performed efficiently. However, we propose a simple Monte Carlo approximation for handling moderately sized cases. Inspired by applications in chemistry, we illustrate the proposed techniques on a real molecular property prediction task in the small data regime.
BaCaDI: Bayesian Causal Discovery with Unknown Interventions
Jun 03, 2022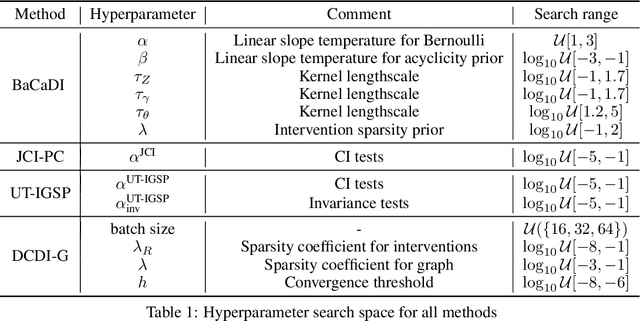
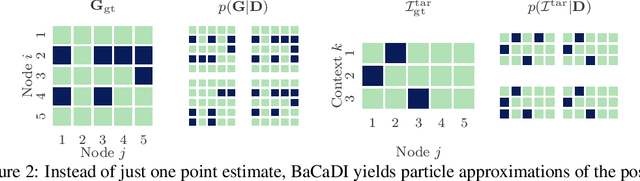
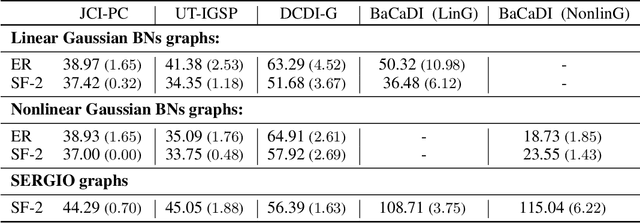
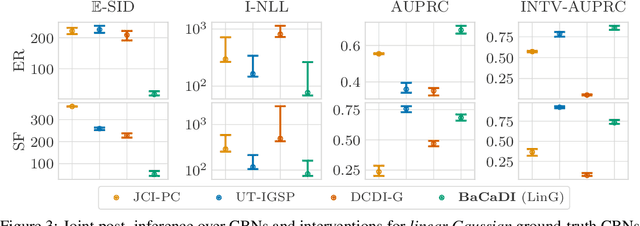
Abstract:Learning causal structures from observation and experimentation is a central task in many domains. For example, in biology, recent advances allow us to obtain single-cell expression data under multiple interventions such as drugs or gene knockouts. However, a key challenge is that often the targets of the interventions are uncertain or unknown. Thus, standard causal discovery methods can no longer be used. To fill this gap, we propose a Bayesian framework (BaCaDI) for discovering the causal structure that underlies data generated under various unknown experimental/interventional conditions. BaCaDI is fully differentiable and operates in the continuous space of latent probabilistic representations of both causal structures and interventions. This enables us to approximate complex posteriors via gradient-based variational inference and to reason about the epistemic uncertainty in the predicted structure. In experiments on synthetic causal discovery tasks and simulated gene-expression data, BaCaDI outperforms related methods in identifying causal structures and intervention targets. Finally, we demonstrate that, thanks to its rigorous Bayesian approach, our method provides well-calibrated uncertainty estimates.
Multi-Scale Representation Learning on Proteins
Apr 04, 2022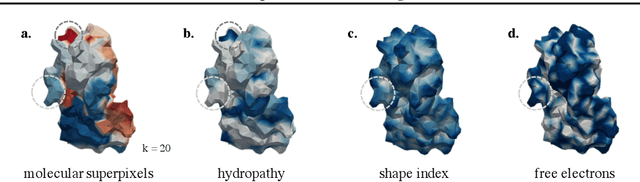
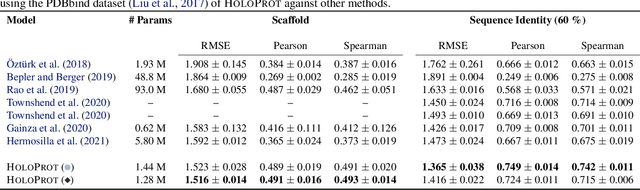
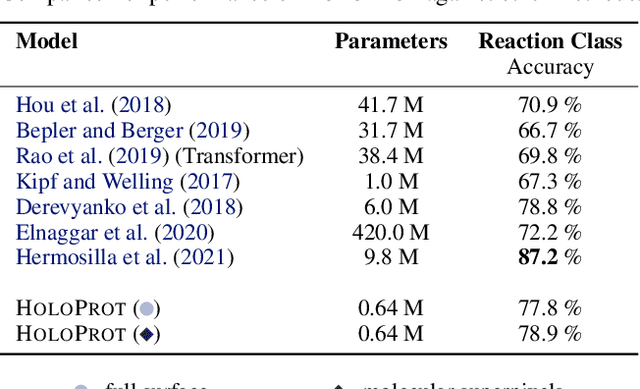
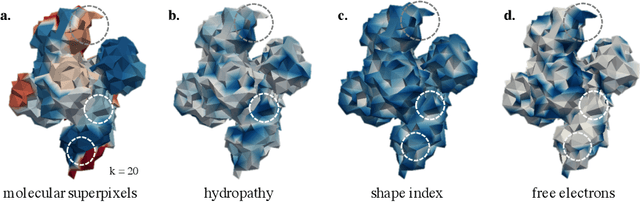
Abstract:Proteins are fundamental biological entities mediating key roles in cellular function and disease. This paper introduces a multi-scale graph construction of a protein -- HoloProt -- connecting surface to structure and sequence. The surface captures coarser details of the protein, while sequence as primary component and structure -- comprising secondary and tertiary components -- capture finer details. Our graph encoder then learns a multi-scale representation by allowing each level to integrate the encoding from level(s) below with the graph at that level. We test the learned representation on different tasks, (i.) ligand binding affinity (regression), and (ii.) protein function prediction (classification). On the regression task, contrary to previous methods, our model performs consistently and reliably across different dataset splits, outperforming all baselines on most splits. On the classification task, it achieves a performance close to the top-performing model while using 10x fewer parameters. To improve the memory efficiency of our construction, we segment the multiplex protein surface manifold into molecular superpixels and substitute the surface with these superpixels at little to no performance loss.
Learning Graph Models for Template-Free Retrosynthesis
Jun 12, 2020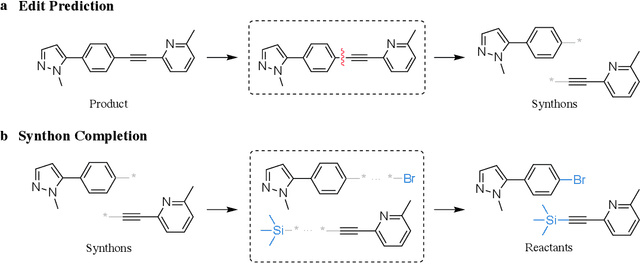
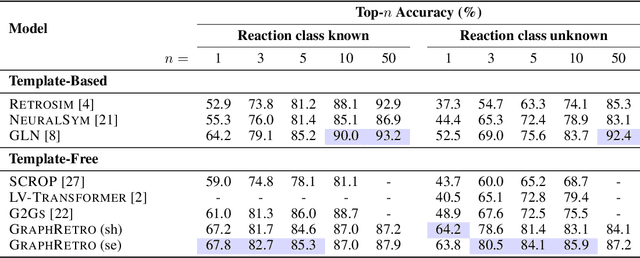
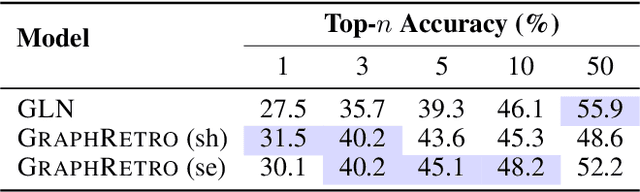
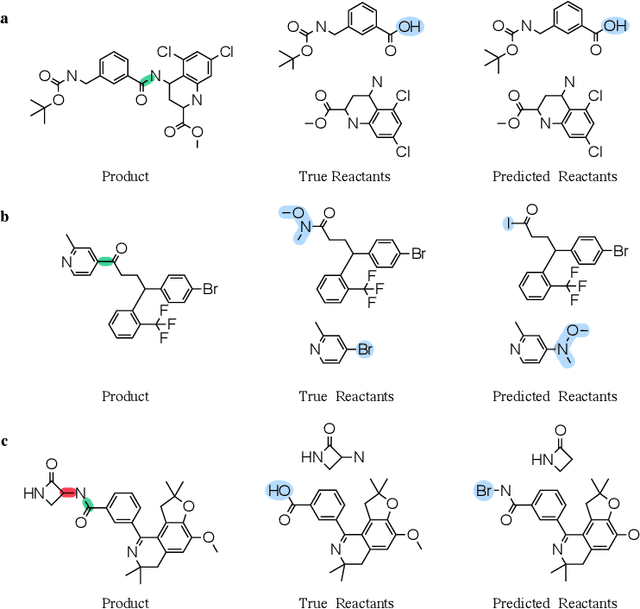
Abstract:Retrosynthesis prediction is a fundamental problem in organic synthesis, where the task is to identify precursor molecules that can be used to synthesize a target molecule. Despite recent advancements in neural retrosynthesis algorithms, they are unable to fully recapitulate the strategies employed by chemists and do not generalize well to infrequent reaction types. In this paper, we propose a graph-based approach that capitalizes on the idea that the graph topology of precursor molecules is largely unaltered during the reaction. The model first predicts the set of graph edits transforming the target into incomplete molecules called synthons. Next, the model learns to expand synthons into complete molecules by attaching relevant leaving groups. Since the model operates at the level of molecular fragments, it avoids full generation, greatly simplifying the underlying architecture and improving its ability to generalize. The model yields $11.7\%$ absolute improvement over state-of-the-art approaches on the USPTO-50k dataset, and a $4\%$ absolute improvement on a rare reaction subset of the same dataset.
Mixture-of-Experts Variational Autoencoder for clustering and generating from similarity-based representations
Oct 17, 2019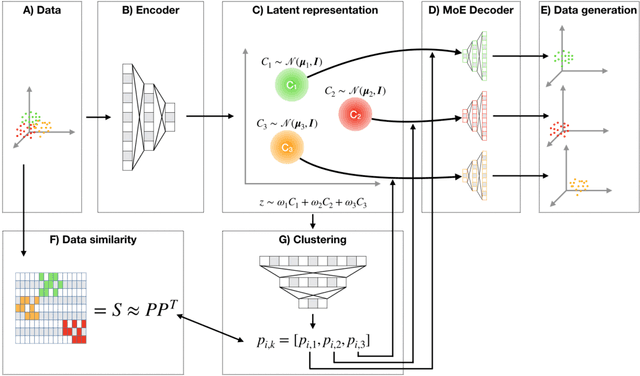
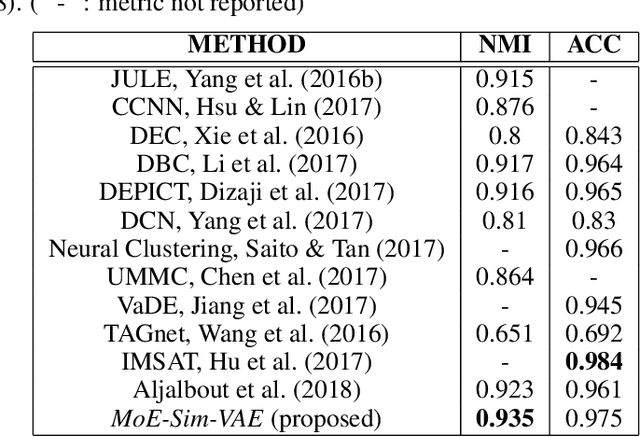
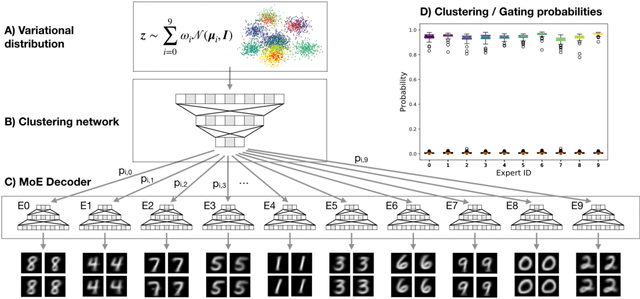
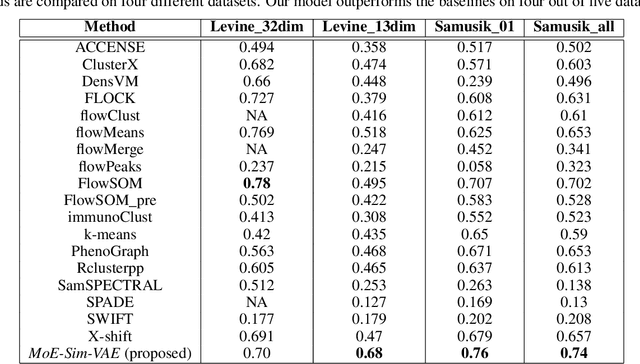
Abstract:Clustering high-dimensional data, such as images or biological measurements, is a long-standing problem and has been studied extensively. Recently, Deep Clustering gained popularity due to the non-linearity of neural networks, which allows for flexibility in fitting the specific peculiarities of complex data. Here we introduce the Mixture-of-Experts Similarity Variational Autoencoder (MoE-Sim-VAE), a novel generative clustering model. The model can learn multi-modal distributions of high-dimensional data and use these to generate realistic data with high efficacy and efficiency. MoE-Sim-VAE is based on a Variational Autoencoder (VAE), where the decoder consists of a Mixture-of-Experts (MoE) architecture. This specific architecture allows for various modes of the data to be automatically learned by means of the experts. Additionally, we encourage the latent representation of our model to follow a Gaussian mixture distribution and to accurately represent the similarities between the data points. We assess the performance of our model on synthetic data, the MNIST benchmark data set, and a challenging real-world task of defining cell subpopulations from mass cytometry (CyTOF) measurements on hundreds of different datasets. MoE-Sim-VAE exhibits superior clustering performance on all these tasks in comparison to the baselines and we show that the MoE architecture in the decoder reduces the computational cost of sampling specific data modes with high fidelity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge