Learning Hamiltonian Flow Maps: Mean Flow Consistency for Large-Timestep Molecular Dynamics

Simulating the long-time evolution of Hamiltonian systems is limited by the small timesteps required for stable numerical integration. To overcome this constraint, we introduce a framework to learn Hamiltonian Flow Maps by predicting the mean phase-space evolution over a chosen time span $Δt$, enabling stable large-timestep updates far beyond the stability limits of classical integrators. To this end, we impose a Mean Flow consistency condition for time-averaged Hamiltonian dynamics. Unlike prior approaches, this allows training on independent phase-space samples without access to future states, avoiding expensive trajectory generation. Validated across diverse Hamiltonian systems, our method in particular improves upon molecular dynamics simulations using machine-learned force fields (MLFF). Our models maintain comparable training and inference cost, but support significantly larger integration timesteps while trained directly on widely-available trajectory-free MLFF datasets.

Doob's Lagrangian: A Sample-Efficient Variational Approach to Transition Path Sampling

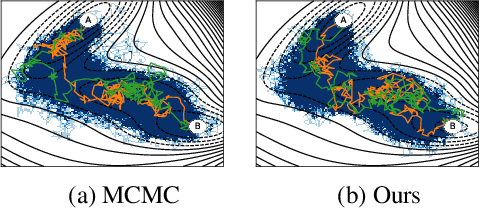
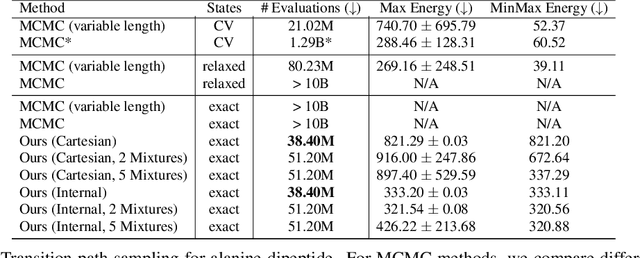
Rare event sampling in dynamical systems is a fundamental problem arising in the natural sciences, which poses significant computational challenges due to an exponentially large space of trajectories. For settings where the dynamical system of interest follows a Brownian motion with known drift, the question of conditioning the process to reach a given endpoint or desired rare event is definitively answered by Doob's h-transform. However, the naive estimation of this transform is infeasible, as it requires simulating sufficiently many forward trajectories to estimate rare event probabilities. In this work, we propose a variational formulation of Doob's $h$-transform as an optimization problem over trajectories between a given initial point and the desired ending point. To solve this optimization, we propose a simulation-free training objective with a model parameterization that imposes the desired boundary conditions by design. Our approach significantly reduces the search space over trajectories and avoids expensive trajectory simulation and inefficient importance sampling estimators which are required in existing methods. We demonstrate the ability of our method to find feasible transition paths on real-world molecular simulation and protein folding tasks.

Transition Path Sampling with Boltzmann Generator-based MCMC Moves

Sampling all possible transition paths between two 3D states of a molecular system has various applications ranging from catalyst design to drug discovery. Current approaches to sample transition paths use Markov chain Monte Carlo and rely on time-intensive molecular dynamics simulations to find new paths. Our approach operates in the latent space of a normalizing flow that maps from the molecule's Boltzmann distribution to a Gaussian, where we propose new paths without requiring molecular simulations. Using alanine dipeptide, we explore Metropolis-Hastings acceptance criteria in the latent space for exact sampling and investigate different latent proposal mechanisms.