sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

Neural timescales from a computational perspective

Timescales of neural activity are diverse across and within brain areas, and experimental observations suggest that neural timescales reflect information in dynamic environments. However, these observations do not specify how neural timescales are shaped, nor whether particular timescales are necessary for neural computations and brain function. Here, we take a complementary perspective and synthesize three directions where computational methods can distill the broad set of empirical observations into quantitative and testable theories: We review (i) how data analysis methods allow us to capture different timescales of neural dynamics across different recording modalities, (ii) how computational models provide a mechanistic explanation for the emergence of diverse timescales, and (iii) how task-optimized models in machine learning uncover the functional relevance of neural timescales. This integrative computational approach, combined with empirical findings, would provide a more holistic understanding of how neural timescales capture the relationship between brain structure, dynamics, and behavior.

A Practical Guide to Statistical Distances for Evaluating Generative Models in Science

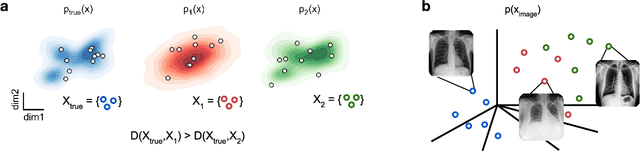
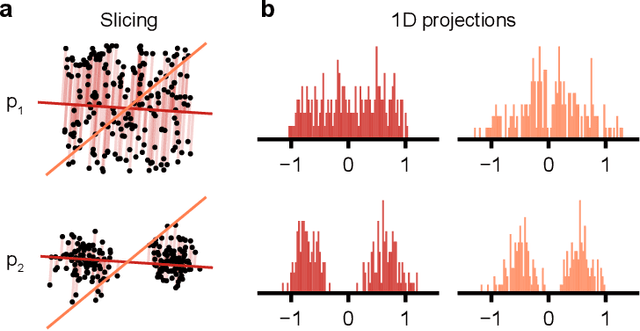
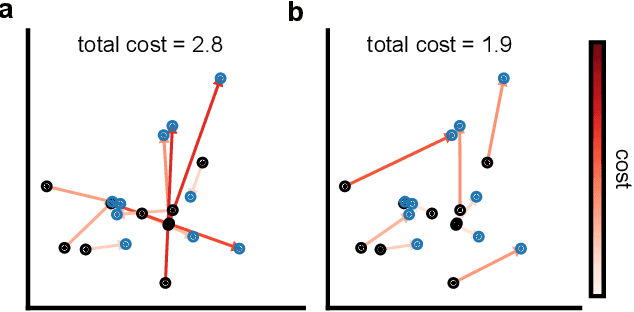
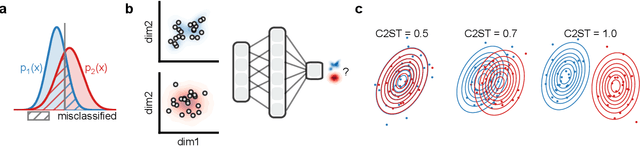
Generative models are invaluable in many fields of science because of their ability to capture high-dimensional and complicated distributions, such as photo-realistic images, protein structures, and connectomes. How do we evaluate the samples these models generate? This work aims to provide an accessible entry point to understanding popular notions of statistical distances, requiring only foundational knowledge in mathematics and statistics. We focus on four commonly used notions of statistical distances representing different methodologies: Using low-dimensional projections (Sliced-Wasserstein; SW), obtaining a distance using classifiers (Classifier Two-Sample Tests; C2ST), using embeddings through kernels (Maximum Mean Discrepancy; MMD), or neural networks (Fr\'echet Inception Distance; FID). We highlight the intuition behind each distance and explain their merits, scalability, complexity, and pitfalls. To demonstrate how these distances are used in practice, we evaluate generative models from different scientific domains, namely a model of decision making and a model generating medical images. We showcase that distinct distances can give different results on similar data. Through this guide, we aim to help researchers to use, interpret, and evaluate statistical distances for generative models in science.

Sourcerer: Sample-based Maximum Entropy Source Distribution Estimation

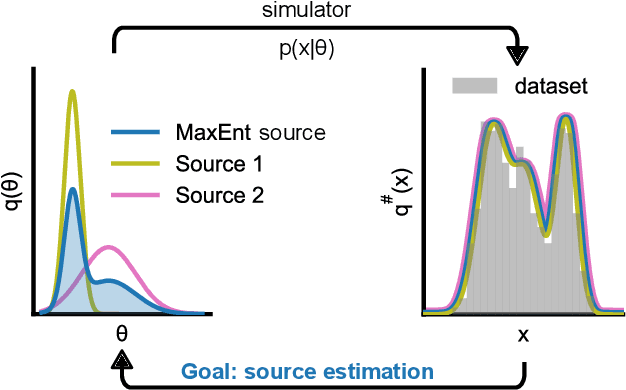
Scientific modeling applications often require estimating a distribution of parameters consistent with a dataset of observations - an inference task also known as source distribution estimation. This problem can be ill-posed, however, since many different source distributions might produce the same distribution of data-consistent simulations. To make a principled choice among many equally valid sources, we propose an approach which targets the maximum entropy distribution, i.e., prioritizes retaining as much uncertainty as possible. Our method is purely sample-based - leveraging the Sliced-Wasserstein distance to measure the discrepancy between the dataset and simulations - and thus suitable for simulators with intractable likelihoods. We benchmark our method on several tasks, and show that it can recover source distributions with substantially higher entropy without sacrificing the fidelity of the simulations. Finally, to demonstrate the utility of our approach, we infer source distributions for parameters of the Hodgkin-Huxley neuron model from experimental datasets with thousands of measurements. In summary, we propose a principled framework for inferring unique source distributions of scientific simulator parameters while retaining as much uncertainty as possible.

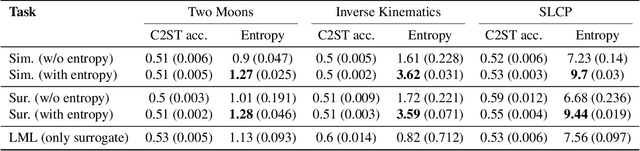
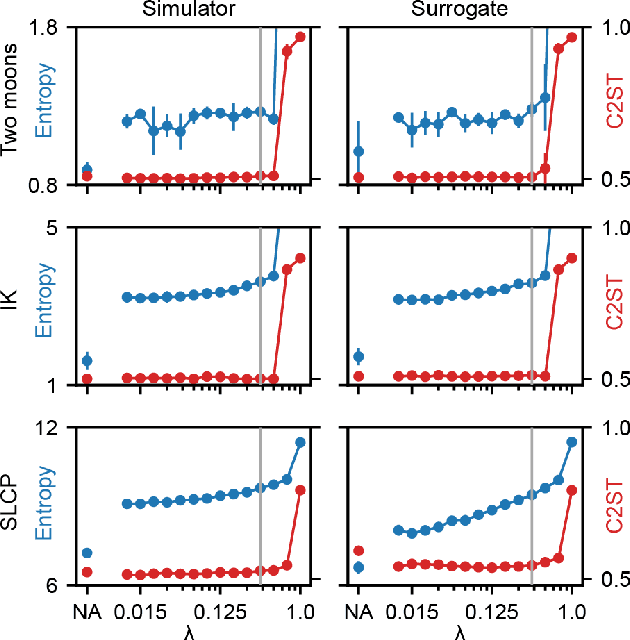
Generalized Bayesian Inference for Scientific Simulators via Amortized Cost Estimation

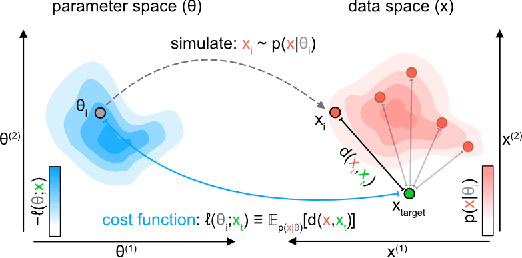
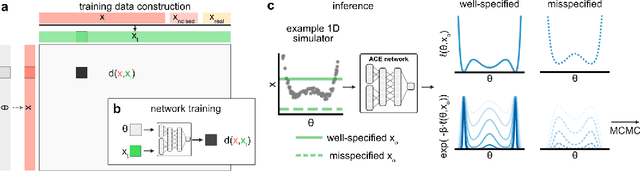
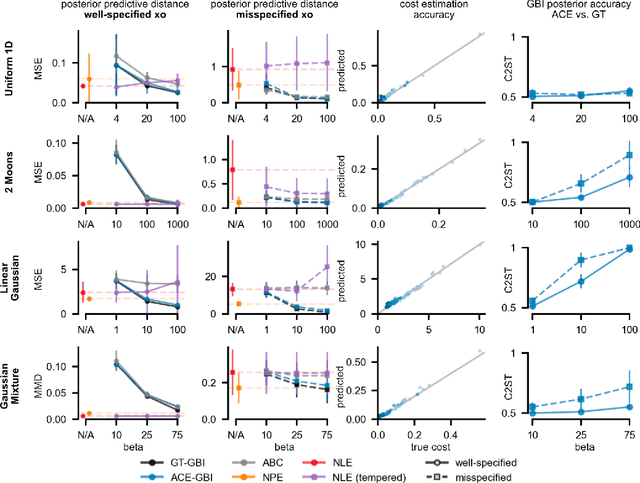
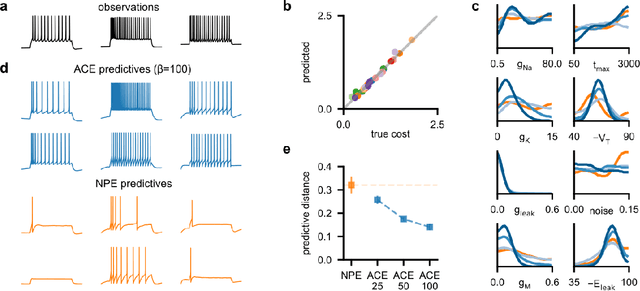
Simulation-based inference (SBI) enables amortized Bayesian inference for simulators with implicit likelihoods. But when we are primarily interested in the quality of predictive simulations, or when the model cannot exactly reproduce the observed data (i.e., is misspecified), targeting the Bayesian posterior may be overly restrictive. Generalized Bayesian Inference (GBI) aims to robustify inference for (misspecified) simulator models, replacing the likelihood-function with a cost function that evaluates the goodness of parameters relative to data. However, GBI methods generally require running multiple simulations to estimate the cost function at each parameter value during inference, making the approach computationally infeasible for even moderately complex simulators. Here, we propose amortized cost estimation (ACE) for GBI to address this challenge: We train a neural network to approximate the cost function, which we define as the expected distance between simulations produced by a parameter and observed data. The trained network can then be used with MCMC to infer GBI posteriors for any observation without running additional simulations. We show that, on several benchmark tasks, ACE accurately predicts cost and provides predictive simulations that are closer to synthetic observations than other SBI methods, especially for misspecified simulators. Finally, we apply ACE to infer parameters of the Hodgkin-Huxley model given real intracellular recordings from the Allen Cell Types Database. ACE identifies better data-matching parameters while being an order of magnitude more simulation-efficient than a standard SBI method. In summary, ACE combines the strengths of SBI methods and GBI to perform robust and simulation-amortized inference for scientific simulators.

SoK: Vehicle Orientation Representations for Deep Rotation Estimation

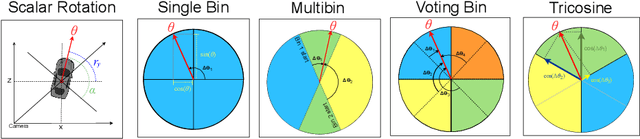
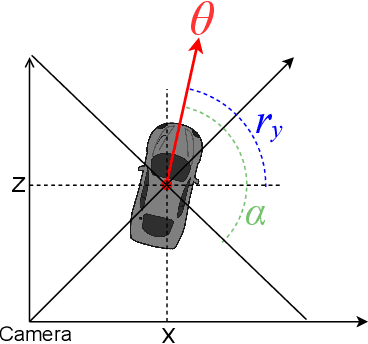
In recent years, there is an influx of deep learning models for 3D vehicle object detection. However, little attention was paid to orientation prediction. Existing research work proposed various vehicle orientation representation methods for deep learning, however a holistic, systematic review has not been conducted. Through our experiments, we categorize and compare the accuracy performance of various existing orientation representations using the KITTI 3D object detection dataset, and propose a new form of orientation representation: Tricosine. Among these, the 2D Cartesian-based representation, or Single Bin, achieves the highest accuracy, with additional channeled inputs (positional encoding and depth map) not boosting prediction performance. Our code is published on GitHub: https://github.com/umd-fire-coml/KITTI-orientation-learning