Cornelius Schröder
FNOPE: Simulation-based inference on function spaces with Fourier Neural Operators
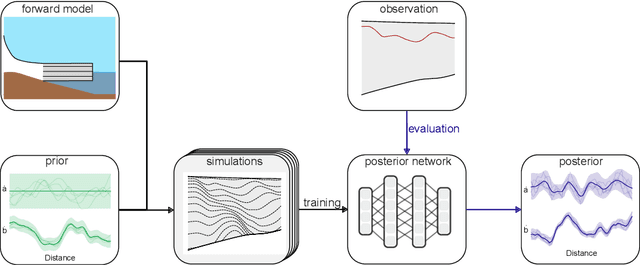
May 28, 2025Abstract:Simulation-based inference (SBI) is an established approach for performing Bayesian inference on scientific simulators. SBI so far works best on low-dimensional parametric models. However, it is difficult to infer function-valued parameters, which frequently occur in disciplines that model spatiotemporal processes such as the climate and earth sciences. Here, we introduce an approach for efficient posterior estimation, using a Fourier Neural Operator (FNO) architecture with a flow matching objective. We show that our approach, FNOPE, can perform inference of function-valued parameters at a fraction of the simulation budget of state of the art methods. In addition, FNOPE supports posterior evaluation at arbitrary discretizations of the domain, as well as simultaneous estimation of vector-valued parameters. We demonstrate the effectiveness of our approach on several benchmark tasks and a challenging spatial inference task from glaciology. FNOPE extends the applicability of SBI methods to new scientific domains by enabling the inference of function-valued parameters.
sbi reloaded: a toolkit for simulation-based inference workflows
Nov 26, 2024
Abstract:Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.
A Practical Guide to Statistical Distances for Evaluating Generative Models in Science
Mar 19, 2024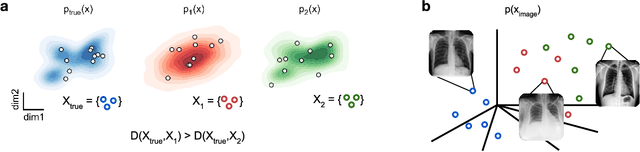
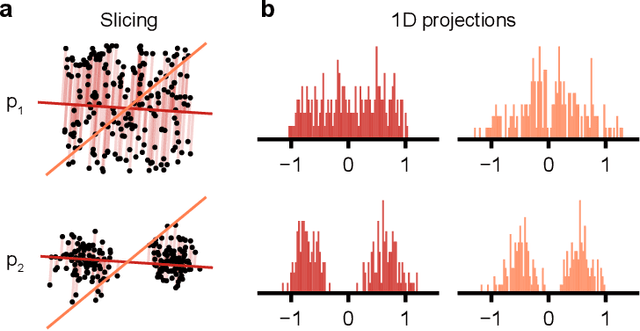
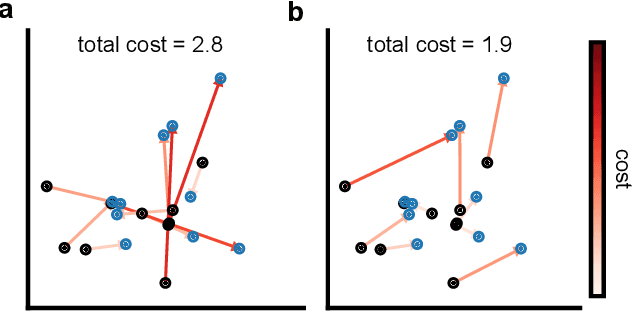
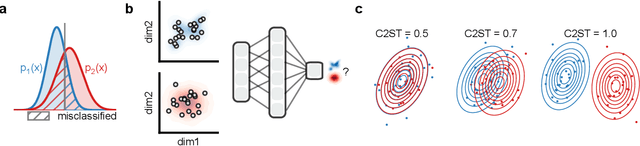
Abstract:Generative models are invaluable in many fields of science because of their ability to capture high-dimensional and complicated distributions, such as photo-realistic images, protein structures, and connectomes. How do we evaluate the samples these models generate? This work aims to provide an accessible entry point to understanding popular notions of statistical distances, requiring only foundational knowledge in mathematics and statistics. We focus on four commonly used notions of statistical distances representing different methodologies: Using low-dimensional projections (Sliced-Wasserstein; SW), obtaining a distance using classifiers (Classifier Two-Sample Tests; C2ST), using embeddings through kernels (Maximum Mean Discrepancy; MMD), or neural networks (Fr\'echet Inception Distance; FID). We highlight the intuition behind each distance and explain their merits, scalability, complexity, and pitfalls. To demonstrate how these distances are used in practice, we evaluate generative models from different scientific domains, namely a model of decision making and a model generating medical images. We showcase that distinct distances can give different results on similar data. Through this guide, we aim to help researchers to use, interpret, and evaluate statistical distances for generative models in science.
Sourcerer: Sample-based Maximum Entropy Source Distribution Estimation
Feb 12, 2024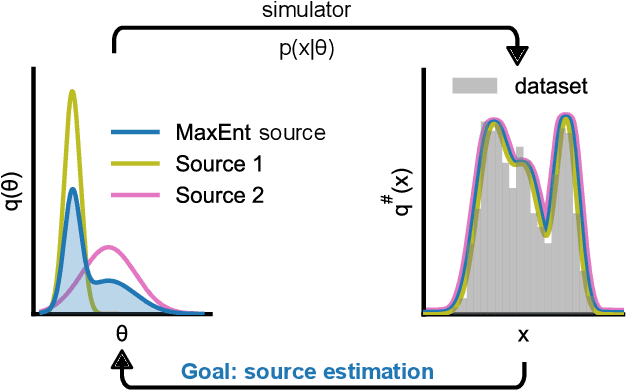
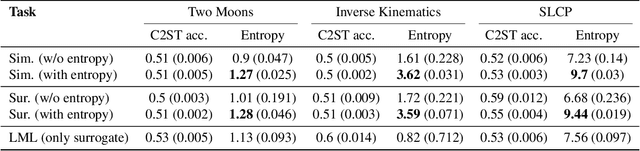

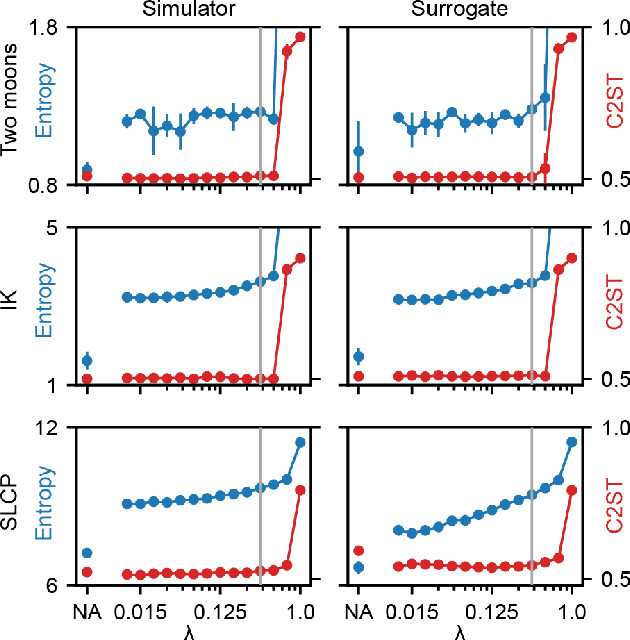
Abstract:Scientific modeling applications often require estimating a distribution of parameters consistent with a dataset of observations - an inference task also known as source distribution estimation. This problem can be ill-posed, however, since many different source distributions might produce the same distribution of data-consistent simulations. To make a principled choice among many equally valid sources, we propose an approach which targets the maximum entropy distribution, i.e., prioritizes retaining as much uncertainty as possible. Our method is purely sample-based - leveraging the Sliced-Wasserstein distance to measure the discrepancy between the dataset and simulations - and thus suitable for simulators with intractable likelihoods. We benchmark our method on several tasks, and show that it can recover source distributions with substantially higher entropy without sacrificing the fidelity of the simulations. Finally, to demonstrate the utility of our approach, we infer source distributions for parameters of the Hodgkin-Huxley neuron model from experimental datasets with thousands of measurements. In summary, we propose a principled framework for inferring unique source distributions of scientific simulator parameters while retaining as much uncertainty as possible.
Simulation-Based Inference of Surface Accumulation and Basal Melt Rates of an Antarctic Ice Shelf from Isochronal Layers
Dec 03, 2023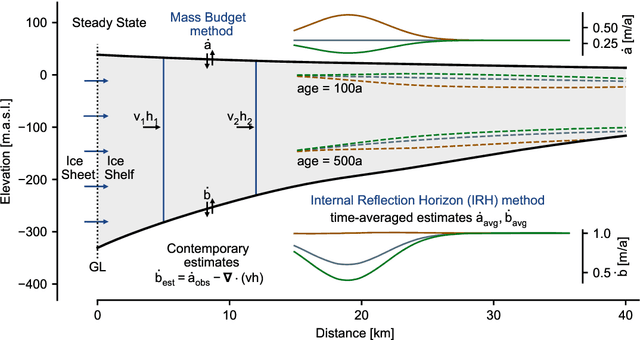
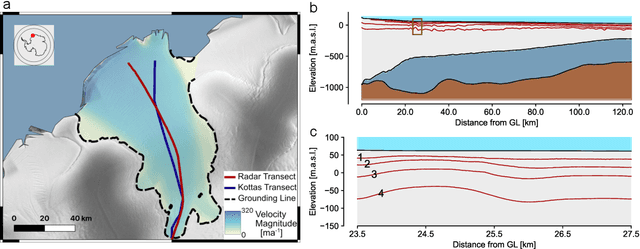
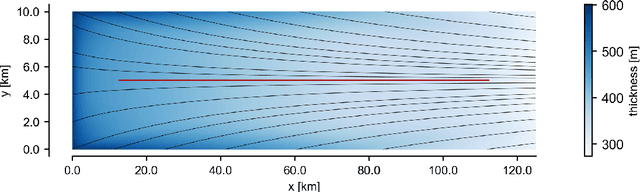
Abstract:The ice shelves buttressing the Antarctic ice sheet determine the rate of ice-discharge into the surrounding oceans. The geometry of ice shelves, and hence their buttressing strength, is determined by ice flow as well as by the local surface accumulation and basal melt rates, governed by atmospheric and oceanic conditions. Contemporary methods resolve one of these rates, but typically not both. Moreover, there is little information of how they changed in time. We present a new method to simultaneously infer the surface accumulation and basal melt rates averaged over decadal and centennial timescales. We infer the spatial dependence of these rates along flow line transects using internal stratigraphy observed by radars, using a kinematic forward model of internal stratigraphy. We solve the inverse problem using simulation-based inference (SBI). SBI performs Bayesian inference by training neural networks on simulations of the forward model to approximate the posterior distribution, allowing us to also quantify uncertainties over the inferred parameters. We demonstrate the validity of our method on a synthetic example, and apply it to Ekstr\"om Ice Shelf, Antarctica, for which newly acquired radar measurements are available. We obtain posterior distributions of surface accumulation and basal melt averaging over 42, 84, 146, and 188 years before 2022. Our results suggest stable atmospheric and oceanographic conditions over this period in this catchment of Antarctica. Use of observed internal stratigraphy can separate the effects of surface accumulation and basal melt, allowing them to be interpreted in a historical context of the last centuries and beyond.
Simultaneous identification of models and parameters of scientific simulators
May 24, 2023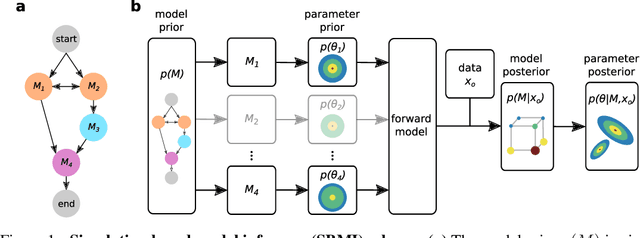

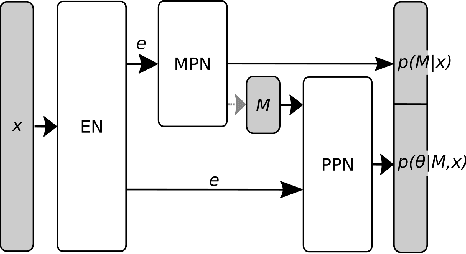

Abstract:Many scientific models are composed of multiple discrete components, and scien tists often make heuristic decisions about which components to include. Bayesian inference provides a mathematical framework for systematically selecting model components, but defining prior distributions over model components and developing associated inference schemes has been challenging. We approach this problem in an amortized simulation-based inference framework: We define implicit model priors over a fixed set of candidate components and train neural networks to infer joint probability distributions over both, model components and associated parameters from simulations. To represent distributions over model components, we introduce a conditional mixture of multivariate binary distributions in the Grassmann formalism. Our approach can be applied to any compositional stochastic simulator without requiring access to likelihood evaluations. We first illustrate our method on a simple time series model with redundant components and show that it can retrieve joint posterior distribution over a set of symbolic expressions and their parameters while accurately capturing redundancy with strongly correlated posteriors. We then apply our approach to drift-diffusion models, a commonly used model class in cognitive neuroscience. After validating the method on synthetic data, we show that our approach explains experimental data as well as previous methods, but that our fully probabilistic approach can help to discover multiple data-consistent model configurations, as well as reveal non-identifiable model components and parameters. Our method provides a powerful tool for data-driven scientific inquiry which will allow scientists to systematically identify essential model components and make uncertainty-informed modelling decisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge