Simultaneous identification of models and parameters of scientific simulators

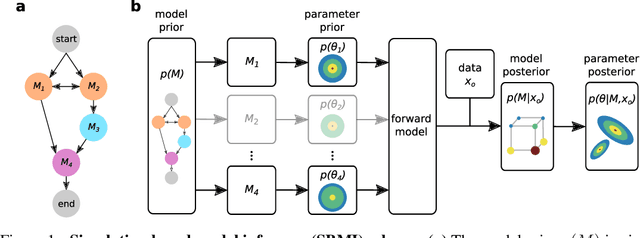
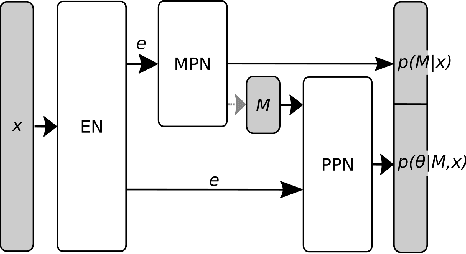
Many scientific models are composed of multiple discrete components, and scien tists often make heuristic decisions about which components to include. Bayesian inference provides a mathematical framework for systematically selecting model components, but defining prior distributions over model components and developing associated inference schemes has been challenging. We approach this problem in an amortized simulation-based inference framework: We define implicit model priors over a fixed set of candidate components and train neural networks to infer joint probability distributions over both, model components and associated parameters from simulations. To represent distributions over model components, we introduce a conditional mixture of multivariate binary distributions in the Grassmann formalism. Our approach can be applied to any compositional stochastic simulator without requiring access to likelihood evaluations. We first illustrate our method on a simple time series model with redundant components and show that it can retrieve joint posterior distribution over a set of symbolic expressions and their parameters while accurately capturing redundancy with strongly correlated posteriors. We then apply our approach to drift-diffusion models, a commonly used model class in cognitive neuroscience. After validating the method on synthetic data, we show that our approach explains experimental data as well as previous methods, but that our fully probabilistic approach can help to discover multiple data-consistent model configurations, as well as reveal non-identifiable model components and parameters. Our method provides a powerful tool for data-driven scientific inquiry which will allow scientists to systematically identify essential model components and make uncertainty-informed modelling decisions.