sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

Diffusion Tempering Improves Parameter Estimation with Probabilistic Integrators for Ordinary Differential Equations

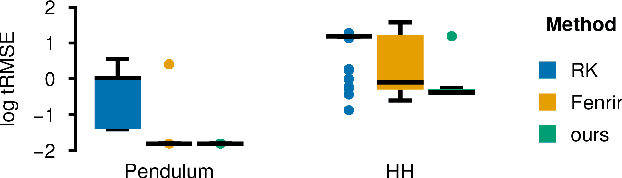
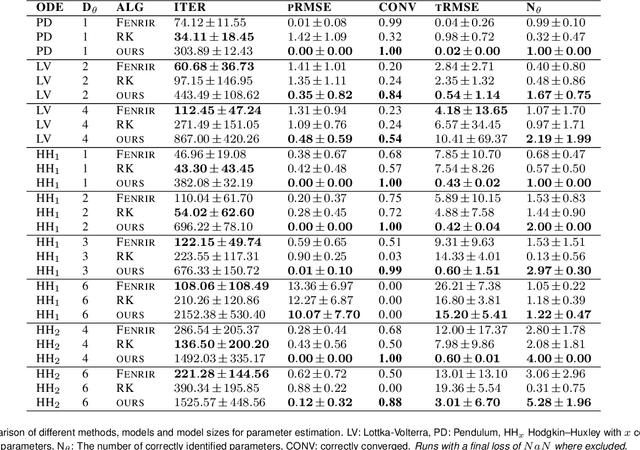
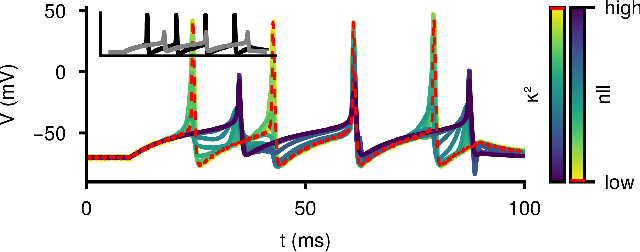
Ordinary differential equations (ODEs) are widely used to describe dynamical systems in science, but identifying parameters that explain experimental measurements is challenging. In particular, although ODEs are differentiable and would allow for gradient-based parameter optimization, the nonlinear dynamics of ODEs often lead to many local minima and extreme sensitivity to initial conditions. We therefore propose diffusion tempering, a novel regularization technique for probabilistic numerical methods which improves convergence of gradient-based parameter optimization in ODEs. By iteratively reducing a noise parameter of the probabilistic integrator, the proposed method converges more reliably to the true parameters. We demonstrate that our method is effective for dynamical systems of different complexity and show that it obtains reliable parameter estimates for a Hodgkin-Huxley model with a practically relevant number of parameters.