Compositional simulation-based inference for time series

Amortized simulation-based inference (SBI) methods train neural networks on simulated data to perform Bayesian inference. While this approach avoids the need for tractable likelihoods, it often requires a large number of simulations and has been challenging to scale to time-series data. Scientific simulators frequently emulate real-world dynamics through thousands of single-state transitions over time. We propose an SBI framework that can exploit such Markovian simulators by locally identifying parameters consistent with individual state transitions. We then compose these local results to obtain a posterior over parameters that align with the entire time series observation. We focus on applying this approach to neural posterior score estimation but also show how it can be applied, e.g., to neural likelihood (ratio) estimation. We demonstrate that our approach is more simulation-efficient than directly estimating the global posterior on several synthetic benchmark tasks and simulators used in ecology and epidemiology. Finally, we validate scalability and simulation efficiency of our approach by applying it to a high-dimensional Kolmogorov flow simulator with around one million dimensions in the data domain.

A Practical Guide to Statistical Distances for Evaluating Generative Models in Science

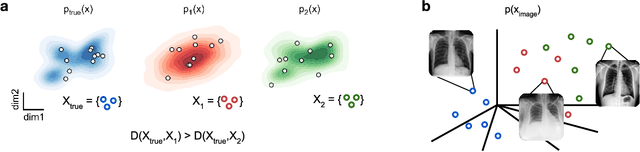
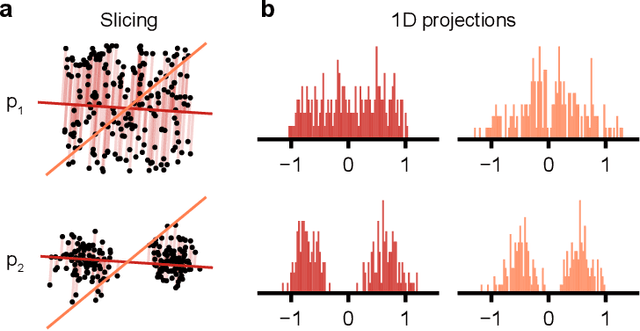
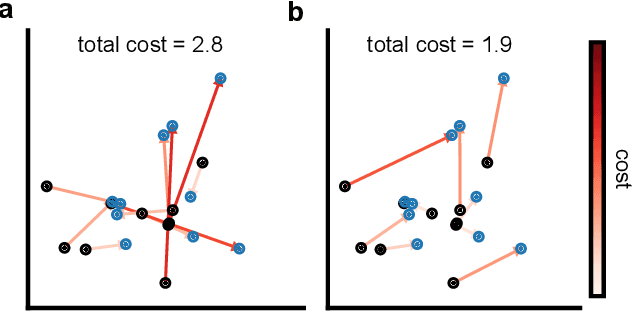
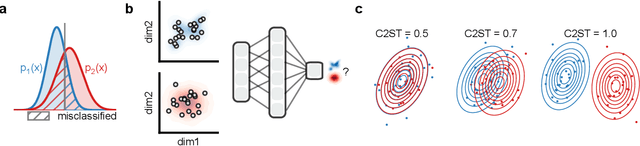
Generative models are invaluable in many fields of science because of their ability to capture high-dimensional and complicated distributions, such as photo-realistic images, protein structures, and connectomes. How do we evaluate the samples these models generate? This work aims to provide an accessible entry point to understanding popular notions of statistical distances, requiring only foundational knowledge in mathematics and statistics. We focus on four commonly used notions of statistical distances representing different methodologies: Using low-dimensional projections (Sliced-Wasserstein; SW), obtaining a distance using classifiers (Classifier Two-Sample Tests; C2ST), using embeddings through kernels (Maximum Mean Discrepancy; MMD), or neural networks (Fr\'echet Inception Distance; FID). We highlight the intuition behind each distance and explain their merits, scalability, complexity, and pitfalls. To demonstrate how these distances are used in practice, we evaluate generative models from different scientific domains, namely a model of decision making and a model generating medical images. We showcase that distinct distances can give different results on similar data. Through this guide, we aim to help researchers to use, interpret, and evaluate statistical distances for generative models in science.

Out-of-Distribution Optimality of Invariant Risk Minimization

Deep Neural Networks often inherit spurious correlations embedded in training data and hence may fail to generalize to unseen domains, which have different distributions from the domain to provide training data. M. Arjovsky et al. (2019) introduced the concept out-of-distribution (o.o.d.) risk, which is the maximum risk among all domains, and formulated the issue caused by spurious correlations as a minimization problem of the o.o.d. risk. Invariant Risk Minimization (IRM) is considered to be a promising approach to minimize the o.o.d. risk: IRM estimates a minimum of the o.o.d. risk by solving a bi-level optimization problem. While IRM has attracted considerable attention with empirical success, it comes with few theoretical guarantees. Especially, a solid theoretical guarantee that the bi-level optimization problem gives the minimum of the o.o.d. risk has not yet been established. Aiming at providing a theoretical justification for IRM, this paper rigorously proves that a solution to the bi-level optimization problem minimizes the o.o.d. risk under certain conditions. The result also provides sufficient conditions on distributions providing training data and on a dimension of feature space for the bi-leveled optimization problem to minimize the o.o.d. risk.

Invariance Learning based on Label Hierarchy

Deep Neural Networks inherit spurious correlations embedded in training data and hence may fail to predict desired labels on unseen domains (or environments), which have different distributions from the domain used in training. Invariance Learning (IL) has been developed recently to overcome this shortcoming; using training data in many domains, IL estimates such a predictor that is invariant to a change of domain. However, the requirement of training data in multiple domains is a strong restriction of IL, since it often needs high annotation cost. We propose a novel IL framework to overcome this problem. Assuming the availability of data from multiple domains for a higher level of classification task, for which the labeling cost is low, we estimate an invariant predictor for the target classification task with training data in a single domain. Additionally, we propose two cross-validation methods for selecting hyperparameters of invariance regularization to solve the issue of hyperparameter selection, which has not been handled properly in existing IL methods. The effectiveness of the proposed framework, including the cross-validation, is demonstrated empirically, and the correctness of the hyperparameter selection is proved under some conditions.