Combined Optimization of Dynamics and Assimilation with End-to-End Learning on Sparse Observations

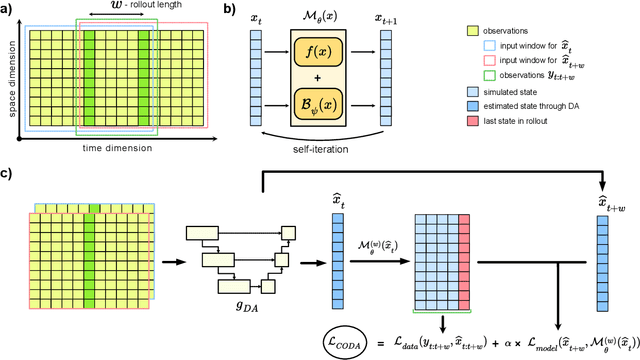
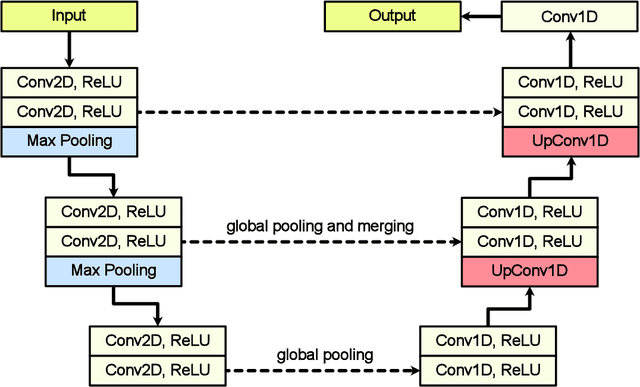
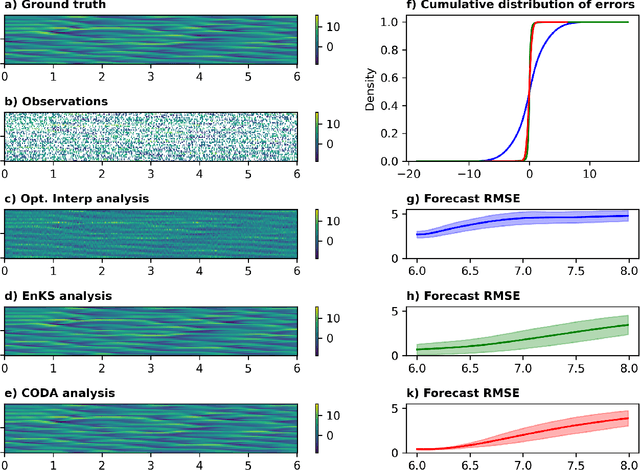
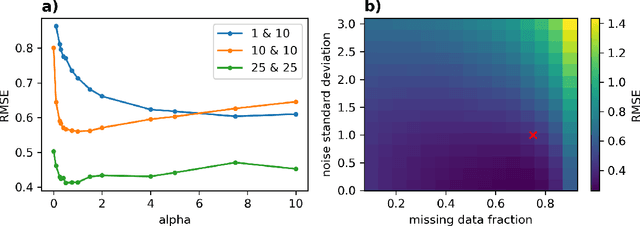
Fitting nonlinear dynamical models to sparse and noisy observations is fundamentally challenging. Identifying dynamics requires data assimilation (DA) to estimate system states, but DA requires an accurate dynamical model. To break this deadlock we present CODA, an end-to-end optimization scheme for jointly learning dynamics and DA directly from sparse and noisy observations. A neural network is trained to carry out data accurate, efficient and parallel-in-time DA, while free parameters of the dynamical system are simultaneously optimized. We carry out end-to-end learning directly on observation data, introducing a novel learning objective that combines unrolled auto-regressive dynamics with the data- and self-consistency terms of weak-constraint 4Dvar DA. By taking into account interactions between new and existing simulation components over multiple time steps, CODA can recover initial conditions, fit unknown dynamical parameters and learn neural network-based PDE terms to match both available observations and self-consistency constraints. In addition to facilitating end-to-end learning of dynamics and providing fast, amortized, non-sequential DA, CODA provides greater robustness to model misspecification than classical DA approaches.

Accelerating the discovery of steady-states of planetary interior dynamics with machine learning

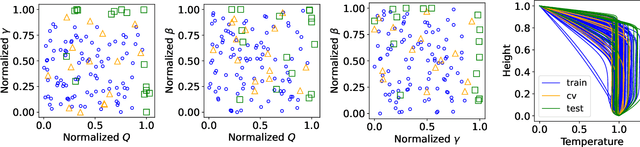
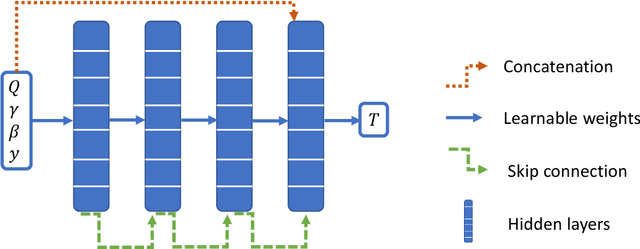
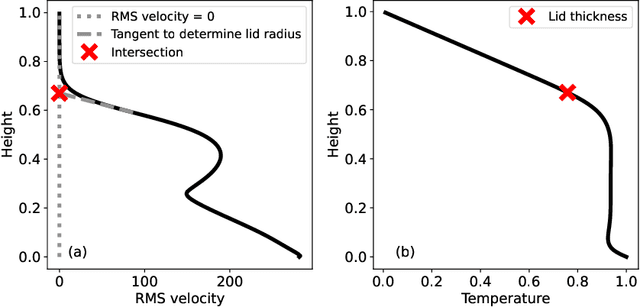
Simulating mantle convection often requires reaching a computationally expensive steady-state, crucial for deriving scaling laws for thermal and dynamical flow properties and benchmarking numerical solutions. The strong temperature dependence of the rheology of mantle rocks causes viscosity variations of several orders of magnitude, leading to a slow-evolving stagnant lid where heat conduction dominates, overlying a rapidly-evolving and strongly convecting region. Time-stepping methods, while effective for fluids with constant viscosity, are hindered by the Courant criterion, which restricts the time step based on the system's maximum velocity and grid size. Consequently, achieving steady-state requires a large number of time steps due to the disparate time scales governing the stagnant and convecting regions. We present a concept for accelerating mantle convection simulations using machine learning. We generate a dataset of 128 two-dimensional simulations with mixed basal and internal heating, and pressure- and temperature-dependent viscosity. We train a feedforward neural network on 97 simulations to predict steady-state temperature profiles. These can then be used to initialize numerical time stepping methods for different simulation parameters. Compared to typical initializations, the number of time steps required to reach steady-state is reduced by a median factor of 3.75. The benefit of this method lies in requiring very few simulations to train on, providing a solution with no prediction error as we initialize a numerical method, and posing minimal computational overhead at inference time. We demonstrate the effectiveness of our approach and discuss the potential implications for accelerated simulations for advancing mantle convection research.

GATSBI: Generative Adversarial Training for Simulation-Based Inference

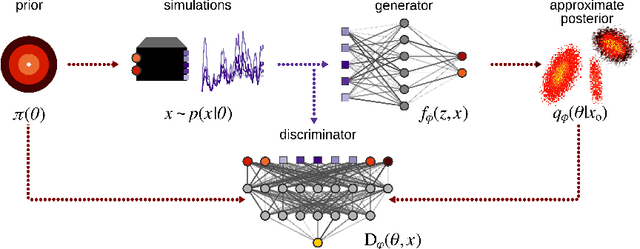
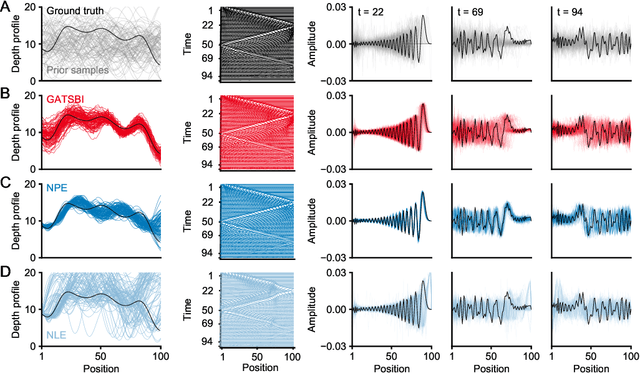
Simulation-based inference (SBI) refers to statistical inference on stochastic models for which we can generate samples, but not compute likelihoods. Like SBI algorithms, generative adversarial networks (GANs) do not require explicit likelihoods. We study the relationship between SBI and GANs, and introduce GATSBI, an adversarial approach to SBI. GATSBI reformulates the variational objective in an adversarial setting to learn implicit posterior distributions. Inference with GATSBI is amortised across observations, works in high-dimensional posterior spaces and supports implicit priors. We evaluate GATSBI on two SBI benchmark problems and on two high-dimensional simulators. On a model for wave propagation on the surface of a shallow water body, we show that GATSBI can return well-calibrated posterior estimates even in high dimensions. On a model of camera optics, it infers a high-dimensional posterior given an implicit prior, and performs better than a state-of-the-art SBI approach. We also show how GATSBI can be extended to perform sequential posterior estimation to focus on individual observations. Overall, GATSBI opens up opportunities for leveraging advances in GANs to perform Bayesian inference on high-dimensional simulation-based models.

Benchmarking Simulation-Based Inference

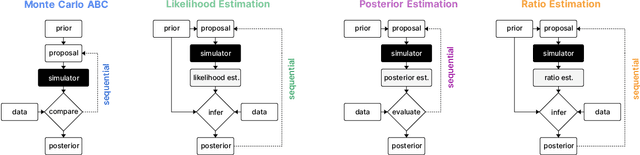
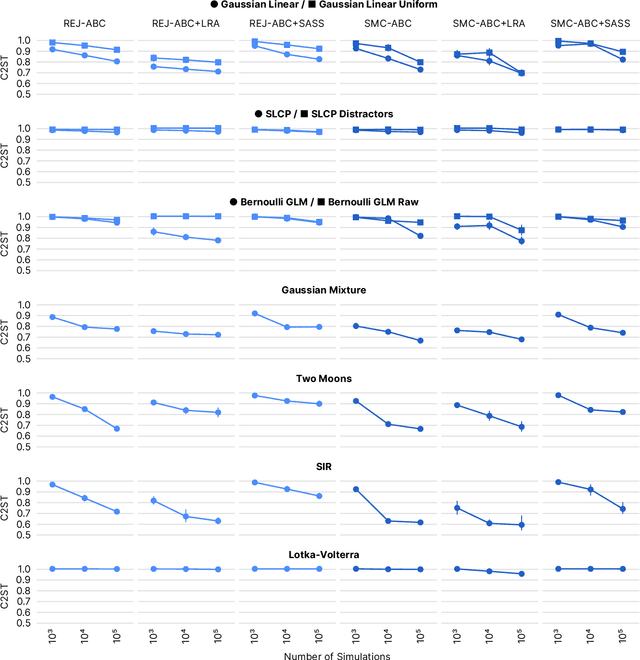
Recent advances in probabilistic modelling have led to a large number of simulation-based inference algorithms which do not require numerical evaluation of likelihoods. However, a public benchmark with appropriate performance metrics for such 'likelihood-free' algorithms has been lacking. This has made it difficult to compare algorithms and identify their strengths and weaknesses. We set out to fill this gap: We provide a benchmark with inference tasks and suitable performance metrics, with an initial selection of algorithms including recent approaches employing neural networks and classical Approximate Bayesian Computation methods. We found that the choice of performance metric is critical, that even state-of-the-art algorithms have substantial room for improvement, and that sequential estimation improves sample efficiency. Neural network-based approaches generally exhibit better performance, but there is no uniformly best algorithm. We provide practical advice and highlight the potential of the benchmark to diagnose problems and improve algorithms. The results can be explored interactively on a companion website. All code is open source, making it possible to contribute further benchmark tasks and inference algorithms.

SBI -- A toolkit for simulation-based inference

Scientists and engineers employ stochastic numerical simulators to model empirically observed phenomena. In contrast to purely statistical models, simulators express scientific principles that provide powerful inductive biases, improve generalization to new data or scenarios and allow for fewer, more interpretable and domain-relevant parameters. Despite these advantages, tuning a simulator's parameters so that its outputs match data is challenging. Simulation-based inference (SBI) seeks to identify parameter sets that a) are compatible with prior knowledge and b) match empirical observations. Importantly, SBI does not seek to recover a single 'best' data-compatible parameter set, but rather to identify all high probability regions of parameter space that explain observed data, and thereby to quantify parameter uncertainty. In Bayesian terminology, SBI aims to retrieve the posterior distribution over the parameters of interest. In contrast to conventional Bayesian inference, SBI is also applicable when one can run model simulations, but no formula or algorithm exists for evaluating the probability of data given parameters, i.e. the likelihood. We present $\texttt{sbi}$, a PyTorch-based package that implements SBI algorithms based on neural networks. $\texttt{sbi}$ facilitates inference on black-box simulators for practising scientists and engineers by providing a unified interface to state-of-the-art algorithms together with documentation and tutorials.

Automatic Posterior Transformation for Likelihood-Free Inference

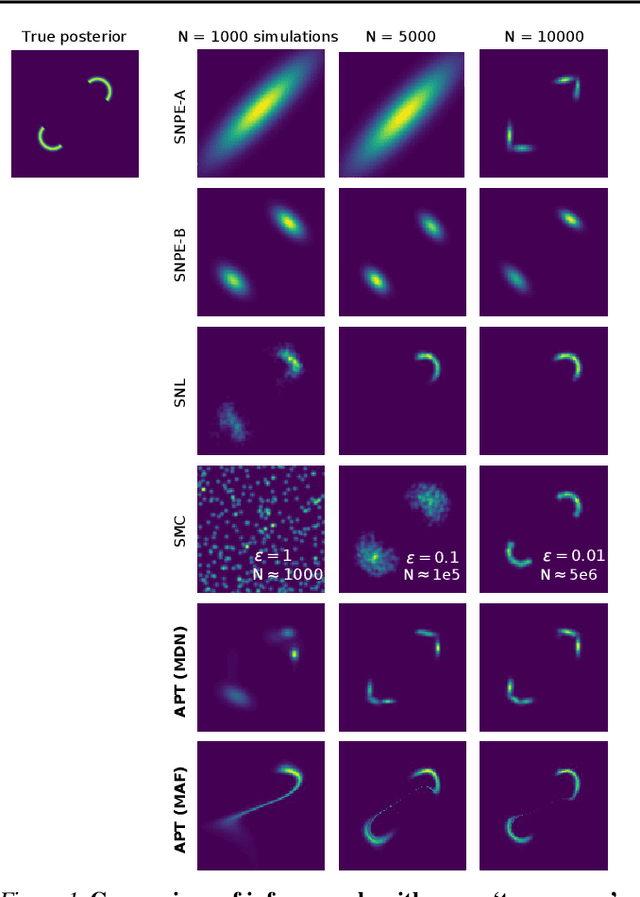
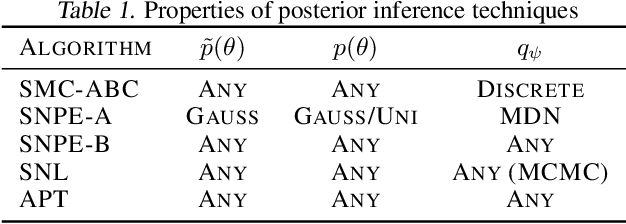
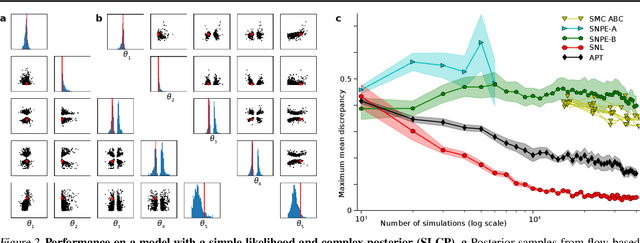
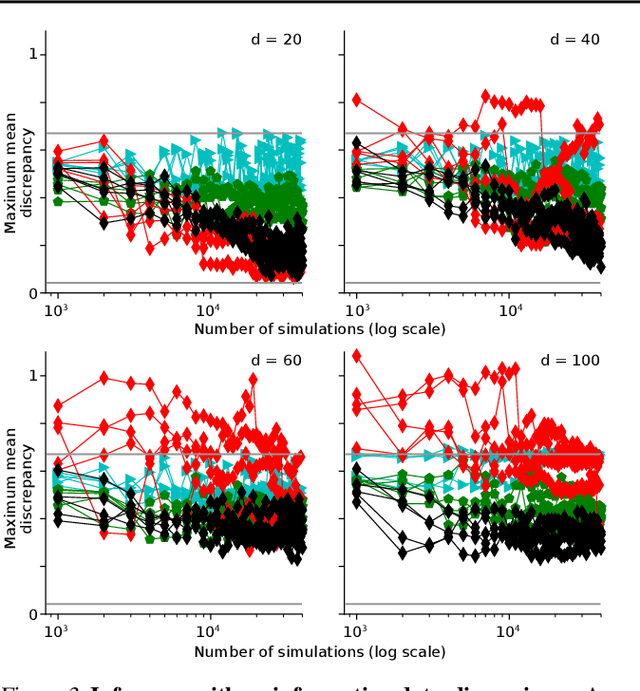
How can one perform Bayesian inference on stochastic simulators with intractable likelihoods? A recent approach is to learn the posterior from adaptively proposed simulations using neural network-based conditional density estimators. However, existing methods are limited to a narrow range of proposal distributions or require importance weighting that can limit performance in practice. Here we present automatic posterior transformation (APT), a new sequential neural posterior estimation method for simulation-based inference. APT can modify the posterior estimate using arbitrary, dynamically updated proposals, and is compatible with powerful flow-based density estimators. It is more flexible, scalable and efficient than previous simulation-based inference techniques. APT can operate directly on high-dimensional time series and image data, opening up new applications for likelihood-free inference.