Physics-based machine learning for mantle convection simulations

Mantle convection simulations are an essential tool for understanding how rocky planets evolve. However, the poorly known input parameters to these simulations, the non-linear dependence of transport properties on pressure and temperature, and the long integration times in excess of several billion years all pose a computational challenge for numerical solvers. We propose a physics-based machine learning approach that predicts creeping flow velocities as a function of temperature while conserving mass, thereby bypassing the numerical solution of the Stokes problem. A finite-volume solver then uses the predicted velocities to advect and diffuse the temperature field to the next time-step, enabling autoregressive rollout at inference. For training, our model requires temperature-velocity snapshots from a handful of simulations (94). We consider mantle convection in a two-dimensional rectangular box with basal and internal heating, pressure- and temperature-dependent viscosity. Overall, our model is up to 89 times faster than the numerical solver. We also show the importance of different components in our convolutional neural network architecture such as mass conservation, learned paddings on the boundaries, and loss scaling for the overall rollout performance. Finally, we test our approach on unseen scenarios to demonstrate some of its strengths and weaknesses.

Accelerating the discovery of steady-states of planetary interior dynamics with machine learning

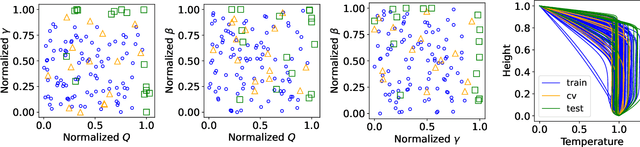
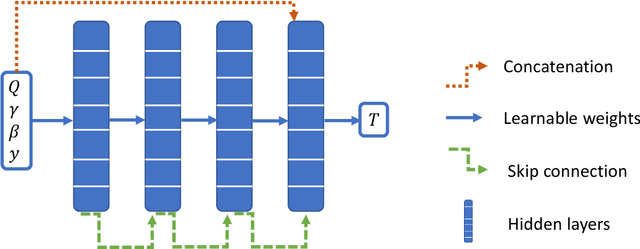
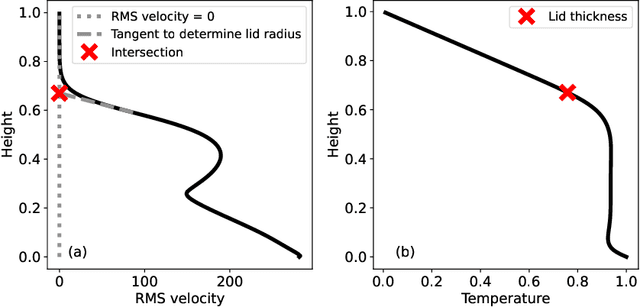
Simulating mantle convection often requires reaching a computationally expensive steady-state, crucial for deriving scaling laws for thermal and dynamical flow properties and benchmarking numerical solutions. The strong temperature dependence of the rheology of mantle rocks causes viscosity variations of several orders of magnitude, leading to a slow-evolving stagnant lid where heat conduction dominates, overlying a rapidly-evolving and strongly convecting region. Time-stepping methods, while effective for fluids with constant viscosity, are hindered by the Courant criterion, which restricts the time step based on the system's maximum velocity and grid size. Consequently, achieving steady-state requires a large number of time steps due to the disparate time scales governing the stagnant and convecting regions. We present a concept for accelerating mantle convection simulations using machine learning. We generate a dataset of 128 two-dimensional simulations with mixed basal and internal heating, and pressure- and temperature-dependent viscosity. We train a feedforward neural network on 97 simulations to predict steady-state temperature profiles. These can then be used to initialize numerical time stepping methods for different simulation parameters. Compared to typical initializations, the number of time steps required to reach steady-state is reduced by a median factor of 3.75. The benefit of this method lies in requiring very few simulations to train on, providing a solution with no prediction error as we initialize a numerical method, and posing minimal computational overhead at inference time. We demonstrate the effectiveness of our approach and discuss the potential implications for accelerated simulations for advancing mantle convection research.

Deep learning for solution and inversion of structural mechanics and vibrations

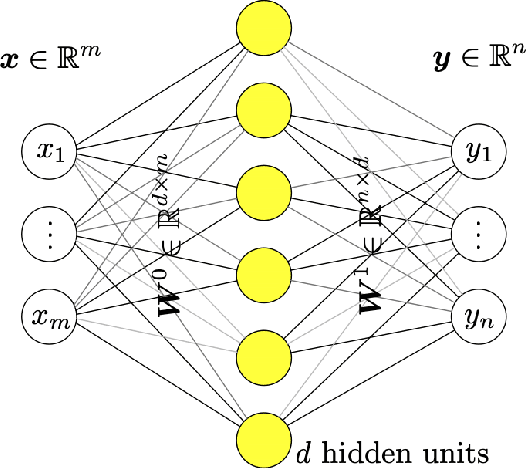
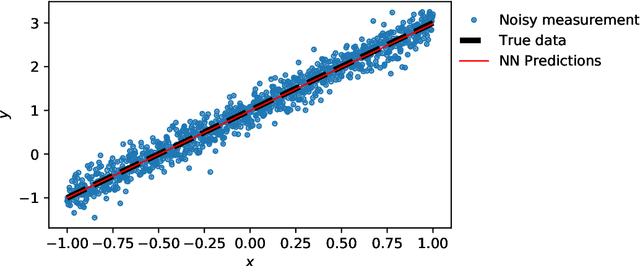
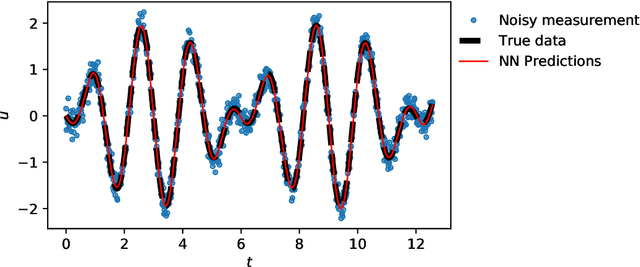
Deep learning has been the most popular machine learning method in the last few years. In this chapter, we present the application of deep learning and physics-informed neural networks concerning structural mechanics and vibration problems. Demonstration problems involve de-noising data, solution to time-dependent ordinary and partial differential equations, and characterizing the system's response for a given data.

A nonlocal physics-informed deep learning framework using the peridynamic differential operator

The Physics-Informed Neural Network (PINN) framework introduced recently incorporates physics into deep learning, and offers a promising avenue for the solution of partial differential equations (PDEs) as well as identification of the equation parameters. The performance of existing PINN approaches, however, may degrade in the presence of sharp gradients, as a result of the inability of the network to capture the solution behavior globally. We posit that this shortcoming may be remedied by introducing long-range (nonlocal) interactions into the network's input, in addition to the short-range (local) space and time variables. Following this ansatz, here we develop a nonlocal PINN approach using the Peridynamic Differential Operator (PDDO)---a numerical method which incorporates long-range interactions and removes spatial derivatives in the governing equations. Because the PDDO functions can be readily incorporated in the neural network architecture, the nonlocality does not degrade the performance of modern deep-learning algorithms. We apply nonlocal PDDO-PINN to the solution and identification of material parameters in solid mechanics and, specifically, to elastoplastic deformation in a domain subjected to indentation by a rigid punch, for which the mixed displacement--traction boundary condition leads to localized deformation and sharp gradients in the solution. We document the superior behavior of nonlocal PINN with respect to local PINN in both solution accuracy and parameter inference, illustrating its potential for simulation and discovery of partial differential equations whose solution develops sharp gradients.