STONet: A novel neural operator for modeling solute transport in micro-cracked reservoirs

In this work, we develop a novel neural operator, the Solute Transport Operator Network (STONet), to efficiently model contaminant transport in micro-cracked reservoirs. The model combines different networks to encode heterogeneous properties effectively. By predicting the concentration rate, we are able to accurately model the transport process. Numerical experiments demonstrate that our neural operator approach achieves accuracy comparable to that of the finite element method. The previously introduced Enriched DeepONet architecture has been revised, motivated by the architecture of the popular multi-head attention of transformers, to improve its performance without increasing the compute cost. The computational efficiency of the proposed model enables rapid and accurate predictions of solute transport, facilitating the optimization of reservoir management strategies and the assessment of environmental impacts. The data and code for the paper will be published at https://github.com/ehsanhaghighat/STONet.

LatticeGraphNet: A two-scale graph neural operator for simulating lattice structures

This study introduces a two-scale Graph Neural Operator (GNO), namely, LatticeGraphNet (LGN), designed as a surrogate model for costly nonlinear finite-element simulations of three-dimensional latticed parts and structures. LGN has two networks: LGN-i, learning the reduced dynamics of lattices, and LGN-ii, learning the mapping from the reduced representation onto the tetrahedral mesh. LGN can predict deformation for arbitrary lattices, therefore the name operator. Our approach significantly reduces inference time while maintaining high accuracy for unseen simulations, establishing the use of GNOs as efficient surrogate models for evaluating mechanical responses of lattices and structures.

Machine Learning-Enabled Precision Position Control and Thermal Regulation in Advanced Thermal Actuators

With their unique combination of characteristics - an energy density almost 100 times that of human muscle, and a power density of 5.3 kW/kg, similar to a jet engine's output - Nylon artificial muscles stand out as particularly apt for robotics applications. However, the necessity of integrating sensors and controllers poses a limitation to their practical usage. Here we report a constant power open-loop controller based on machine learning. We show that we can control the position of a nylon artificial muscle without external sensors. To this end, we construct a mapping from a desired displacement trajectory to a required power using an ensemble encoder-style feed-forward neural network. The neural controller is carefully trained on a physics-based denoised dataset and can be fine-tuned to accommodate various types of thermal artificial muscles, irrespective of the presence or absence of hysteresis.

A novel deeponet model for learning moving-solution operators with applications to earthquake hypocenter localization

Seismicity induced by human activities poses a significant threat to public safety, emphasizing the need for accurate and timely earthquake hypocenter localization. In this study, we introduce X-DeepONet, a novel variant of deep operator networks (DeepONets), for learning moving-solution operators of parametric partial differential equations (PDEs), with application to real-time earthquake localization. Leveraging the power of neural operators, X-DeepONet learns to estimate traveltime fields associated with earthquake sources by incorporating information from seismic arrival times and velocity models. Similar to the DeepONet, X-DeepONet includes a trunk net and a branch net. Additionally, we introduce a root network that not only takes the standard DeepONet's multiplication operator as input, it also takes addition and subtraction operators. We show that for problems with moving fields, the standard multiplication operation of DeepONet is insufficient to capture field relocation, while addition and subtraction operators along with the eXtended root significantly improve its accuracy both under data-driven (supervised) and physics-informed (unsupervised) training. We demonstrate the effectiveness of X-DeepONet through various experiments, including scenarios with variable velocity models and arrival times. The results show remarkable accuracy in earthquake localization, even for heterogeneous and complex velocity models. The proposed framework also exhibits excellent generalization capabilities and robustness against noisy arrival times. The method provides a computationally efficient approach for quantifying uncertainty in hypocenter locations resulting from traveltime pick errors and velocity model variations. Our results underscore X-DeepONet's potential to improve seismic monitoring systems, aiding the development of early warning systems for seismic hazard mitigation.

Inverse modeling of nonisothermal multiphase poromechanics using physics-informed neural networks

We propose a solution strategy for parameter identification in multiphase thermo-hydro-mechanical (THM) processes in porous media using physics-informed neural networks (PINNs). We employ a dimensionless form of the THM governing equations that is particularly well suited for the inverse problem, and we leverage the sequential multiphysics PINN solver we developed in previous work. We validate the proposed inverse-modeling approach on multiple benchmark problems, including Terzaghi's isothermal consolidation problem, Barry-Mercer's isothermal injection-production problem, and nonisothermal consolidation of an unsaturated soil layer. We report the excellent performance of the proposed sequential PINN-THM inverse solver, thus paving the way for the application of PINNs to inverse modeling of complex nonlinear multiphysics problems.

Constitutive model characterization and discovery using physics-informed deep learning

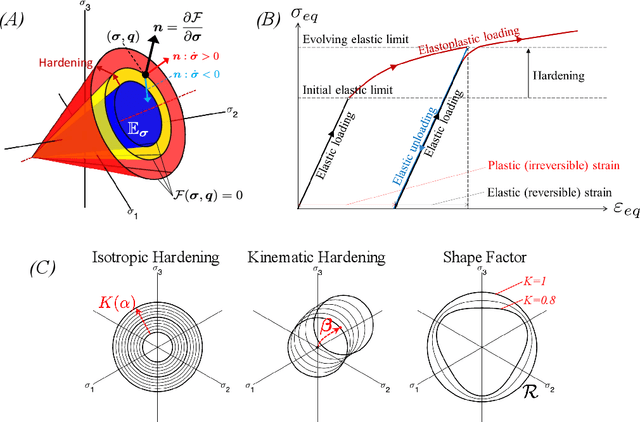
Classically, the mechanical response of materials is described through constitutive models, often in the form of constrained ordinary differential equations. These models have a very limited number of parameters, yet, they are extremely efficient in reproducing complex responses observed in experiments. Additionally, in their discretized form, they are computationally very efficient, often resulting in a simple algebraic relation, and therefore they have been extensively used within large-scale explicit and implicit finite element models. However, it is very challenging to formulate new constitutive models, particularly for materials with complex microstructures such as composites. A recent trend in constitutive modeling leverages complex neural network architectures to construct complex material responses where a constitutive model does not yet exist. Whilst very accurate, they suffer from two deficiencies. First, they are interpolation models and often do poorly in extrapolation. Second, due to their complex architecture and numerous parameters, they are inefficient to be used as a constitutive model within a large-scale finite element model. In this study, we propose a novel approach based on the physics-informed learning machines for the characterization and discovery of constitutive models. Unlike data-driven constitutive models, we leverage foundations of elastoplasticity theory as regularization terms in the total loss function to find parametric constitutive models that are also theoretically sound. We demonstrate that our proposed framework can efficiently identify the underlying constitutive model describing different datasets from the von Mises family.

Physics-informed neural network solution of thermo-hydro-mechanical (THM) processes in porous media

Physics-Informed Neural Networks (PINNs) have received increased interest for forward, inverse, and surrogate modeling of problems described by partial differential equations (PDE). However, their application to multiphysics problem, governed by several coupled PDEs, present unique challenges that have hindered the robustness and widespread applicability of this approach. Here we investigate the application of PINNs to the forward solution of problems involving thermo-hydro-mechanical (THM) processes in porous media, which exhibit disparate spatial and temporal scales in thermal conductivity, hydraulic permeability, and elasticity. In addition, PINNs are faced with the challenges of the multi-objective and non-convex nature of the optimization problem. To address these fundamental issues, we: (1)~rewrite the THM governing equations in dimensionless form that is best suited for deep-learning algorithms; (2)~propose a sequential training strategy that circumvents the need for a simultaneous solution of the multiphysics problem and facilitates the task of optimizers in the solution search; and (3)~leverage adaptive weight strategies to overcome the stiffness in the gradient flow of the multi-objective optimization problem. Finally, we apply this framework to the solution of several synthetic problems in 1D and~2D.

Physics-informed neural network simulation of multiphase poroelasticity using stress-split sequential training

Physics-informed neural networks (PINNs) have received significant attention as a unified framework for forward, inverse, and surrogate modeling of problems governed by partial differential equations (PDEs). Training PINNs for forward problems, however, pose significant challenges, mainly because of the complex non-convex and multi-objective loss function. In this work, we present a PINN approach to solving the equations of coupled flow and deformation in porous media for both single-phase and multiphase flow. To this end, we construct the solution space using multi-layer neural networks. Due to the dynamics of the problem, we find that incorporating multiple differential relations into the loss function results in an unstable optimization problem, meaning that sometimes it converges to the trivial null solution, other times it moves very far from the expected solution. We report a dimensionless form of the coupled governing equations that we find most favourable to the optimizer. Additionally, we propose a sequential training approach based on the stress-split algorithms of poromechanics. Notably, we find that sequential training based on stress-split performs well for different problems, while the classical strain-split algorithm shows an unstable behaviour similar to what is reported in the context of finite element solvers. We use the approach to solve benchmark problems of poroelasticity, including Mandel's consolidation problem, Barry-Mercer's injection-production problem, and a reference two-phase drainage problem. The Python-SciANN codes reproducing the results reported in this manuscript will be made publicly available at https://github.com/sciann/sciann-applications.

A Physics Informed Neural Network Approach to Solution and Identification of Biharmonic Equations of Elasticity

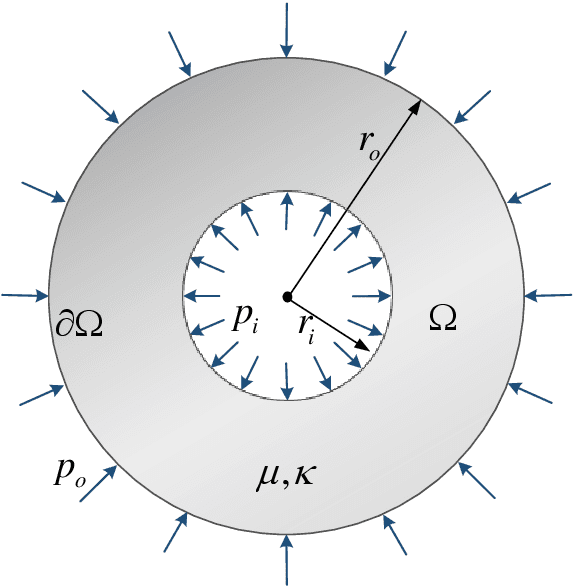
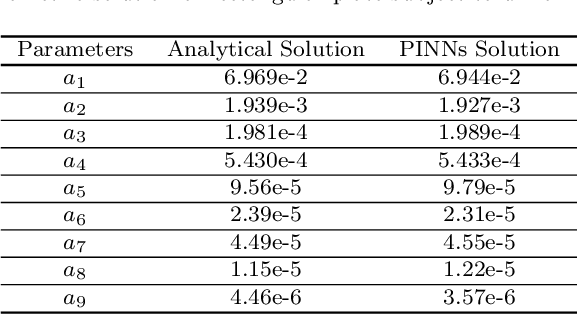
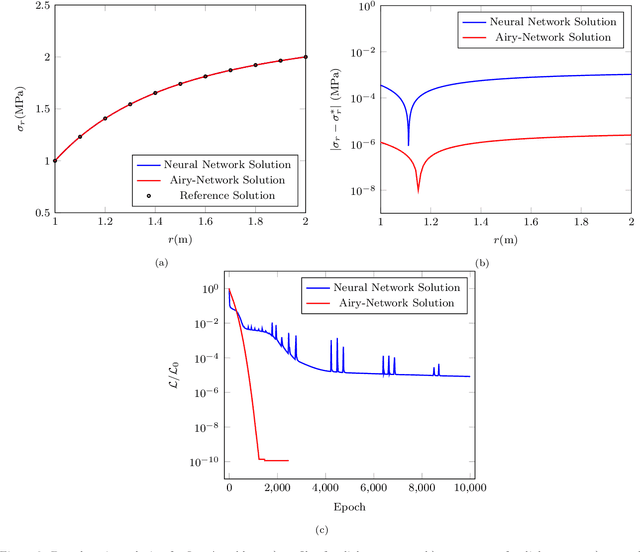
We explore an application of the Physics Informed Neural Networks (PINNs) in conjunction with Airy stress functions and Fourier series to find optimal solutions to a few reference biharmonic problems of elasticity and elastic plate theory. Biharmonic relations are fourth-order partial differential equations (PDEs) that are challenging to solve using classical numerical methods, and have not been addressed using PINNs. Our work highlights a novel application of classical analytical methods to guide the construction of efficient neural networks with the minimal number of parameters that are very accurate and fast to evaluate. In particular, we find that enriching feature space using Airy stress functions can significantly improve the accuracy of PINN solutions for biharmonic PDEs.

Deep learning for solution and inversion of structural mechanics and vibrations

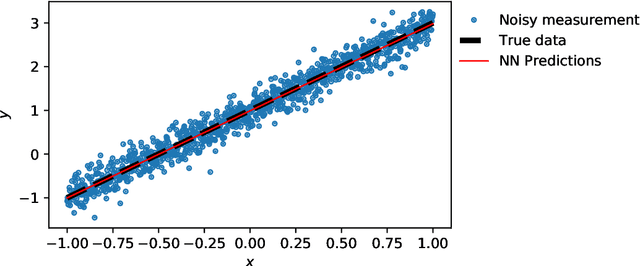
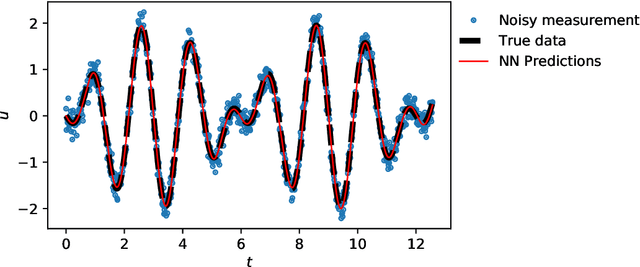
Deep learning has been the most popular machine learning method in the last few years. In this chapter, we present the application of deep learning and physics-informed neural networks concerning structural mechanics and vibration problems. Demonstration problems involve de-noising data, solution to time-dependent ordinary and partial differential equations, and characterizing the system's response for a given data.