Bridging scales in multiscale bubble growth dynamics with correlated fluctuations using neural operator learning

The intricate process of bubble growth dynamics involves a broad spectrum of physical phenomena from microscale mechanics of bubble formation to macroscale interplay between bubbles and surrounding thermo-hydrodynamics. Traditional bubble dynamics models including atomistic approaches and continuum-based methods segment the bubble dynamics into distinct scale-specific models. In order to bridge the gap between microscale stochastic fluid models and continuum-based fluid models for bubble dynamics, we develop a composite neural operator model to unify the analysis of nonlinear bubble dynamics across microscale and macroscale regimes by integrating a many-body dissipative particle dynamics (mDPD) model with a continuum-based Rayleigh-Plesset (RP) model through a novel neural network architecture, which consists of a deep operator network for learning the mean behavior of bubble growth subject to pressure variations and a long short-term memory network for learning the statistical features of correlated fluctuations in microscale bubble dynamics. Training and testing data are generated by conducting mDPD and RP simulations for nonlinear bubble dynamics with initial bubble radii ranging from 0.1 to 1.5 micrometers. Results show that the trained composite neural operator model can accurately predict bubble dynamics across scales, with a 99% accuracy for the time evaluation of the bubble radius under varying external pressure while containing correct size-dependent stochastic fluctuations in microscale bubble growth dynamics. The composite neural operator is the first deep learning surrogate for multiscale bubble growth dynamics that can capture correct stochastic fluctuations in microscopic fluid phenomena, which sets a new direction for future research in multiscale fluid dynamics modeling.

A novel deeponet model for learning moving-solution operators with applications to earthquake hypocenter localization

Seismicity induced by human activities poses a significant threat to public safety, emphasizing the need for accurate and timely earthquake hypocenter localization. In this study, we introduce X-DeepONet, a novel variant of deep operator networks (DeepONets), for learning moving-solution operators of parametric partial differential equations (PDEs), with application to real-time earthquake localization. Leveraging the power of neural operators, X-DeepONet learns to estimate traveltime fields associated with earthquake sources by incorporating information from seismic arrival times and velocity models. Similar to the DeepONet, X-DeepONet includes a trunk net and a branch net. Additionally, we introduce a root network that not only takes the standard DeepONet's multiplication operator as input, it also takes addition and subtraction operators. We show that for problems with moving fields, the standard multiplication operation of DeepONet is insufficient to capture field relocation, while addition and subtraction operators along with the eXtended root significantly improve its accuracy both under data-driven (supervised) and physics-informed (unsupervised) training. We demonstrate the effectiveness of X-DeepONet through various experiments, including scenarios with variable velocity models and arrival times. The results show remarkable accuracy in earthquake localization, even for heterogeneous and complex velocity models. The proposed framework also exhibits excellent generalization capabilities and robustness against noisy arrival times. The method provides a computationally efficient approach for quantifying uncertainty in hypocenter locations resulting from traveltime pick errors and velocity model variations. Our results underscore X-DeepONet's potential to improve seismic monitoring systems, aiding the development of early warning systems for seismic hazard mitigation.

Physics-Informed Computer Vision: A Review and Perspectives

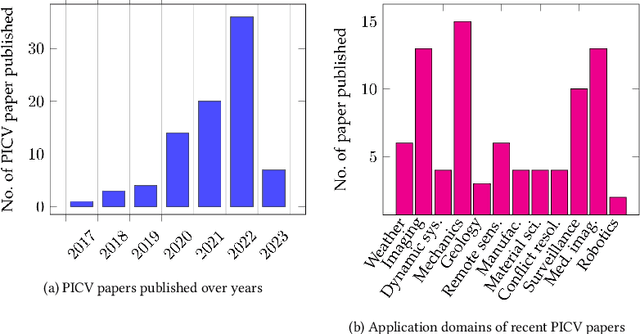
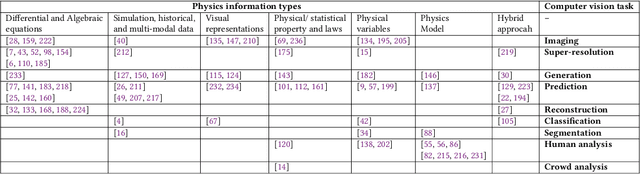
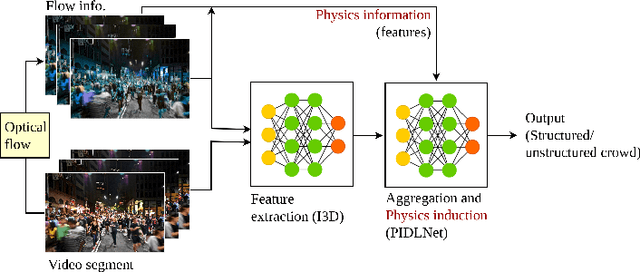
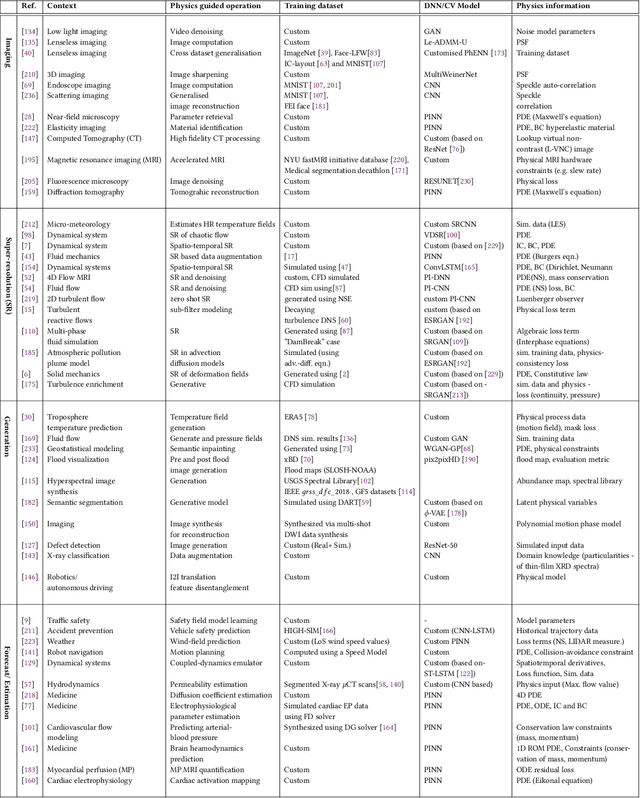
Incorporation of physical information in machine learning frameworks are opening and transforming many application domains. Here the learning process is augmented through the induction of fundamental knowledge and governing physical laws. In this work we explore their utility for computer vision tasks in interpreting and understanding visual data. We present a systematic literature review of formulation and approaches to computer vision tasks guided by physical laws. We begin by decomposing the popular computer vision pipeline into a taxonomy of stages and investigate approaches to incorporate governing physical equations in each stage. Existing approaches in each task are analyzed with regard to what governing physical processes are modeled, formulated and how they are incorporated, i.e. modify data (observation bias), modify networks (inductive bias), and modify losses (learning bias). The taxonomy offers a unified view of the application of the physics-informed capability, highlighting where physics-informed learning has been conducted and where the gaps and opportunities are. Finally, we highlight open problems and challenges to inform future research. While still in its early days, the study of physics-informed computer vision has the promise to develop better computer vision models that can improve physical plausibility, accuracy, data efficiency and generalization in increasingly realistic applications.

Splitting physics-informed neural networks for inferring the dynamics of integer- and fractional-order neuron models

We introduce a new approach for solving forward systems of differential equations using a combination of splitting methods and physics-informed neural networks (PINNs). The proposed method, splitting PINN, effectively addresses the challenge of applying PINNs to forward dynamical systems and demonstrates improved accuracy through its application to neuron models. Specifically, we apply operator splitting to decompose the original neuron model into sub-problems that are then solved using PINNs. Moreover, we develop an $L^1$ scheme for discretizing fractional derivatives in fractional neuron models, leading to improved accuracy and efficiency. The results of this study highlight the potential of splitting PINNs in solving both integer- and fractional-order neuron models, as well as other similar systems in computational science and engineering.

Machine Learning in Heterogeneous Porous Materials

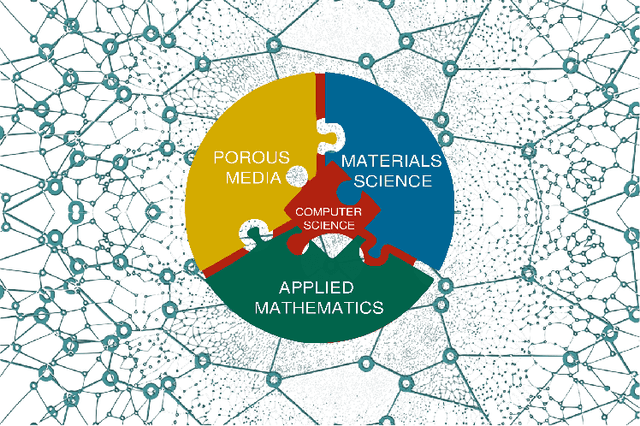
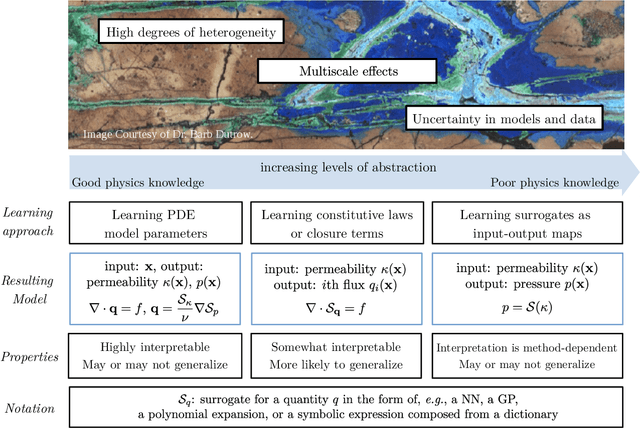
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

A physics-informed variational DeepONet for predicting the crack path in brittle materials

Failure trajectories, identifying the probable failure zones, and damage statistics are some of the key quantities of relevance in brittle fracture applications. High-fidelity numerical solvers that reliably estimate these relevant quantities exist but they are computationally demanding requiring a high resolution of the crack. Moreover, independent intensive simulations need to be carried out even for a small change in domain parameters and/or material properties. Therefore, fast and generalizable surrogate models are needed to alleviate the computational burden but the discontinuous nature of fracture mechanics presents a major challenge to developing such models. We propose a physics-informed variational formulation of DeepONet (V-DeepONet) for brittle fracture analysis. V-DeepONet is trained to map the initial configuration of the defect to the relevant fields of interests (e.g., damage and displacement fields). Once the network is trained, the entire global solution can be rapidly obtained for any initial crack configuration and loading steps on that domain. While the original DeepONet is solely data-driven, we take a different path to train the V-DeepONet by imposing the governing equations in variational form and we also use some labelled data. We demonstrate the effectiveness of V-DeepOnet through two benchmarks of brittle fracture, and we verify its accuracy using results from high-fidelity solvers. Encoding the physical laws and also some data to train the network renders the surrogate model capable of accurately performing both interpolation and extrapolation tasks, considering that fracture modeling is very sensitive to fluctuations. The proposed hybrid training of V-DeepONet is superior to state-of-the-art methods and can be applied to a wide array of dynamical systems with complex responses.

Learning functionals via LSTM neural networks for predicting vessel dynamics in extreme sea states

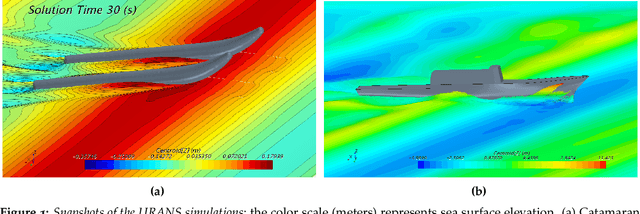
Predicting motions of vessels in extreme sea states represents one of the most challenging problems in naval hydrodynamics. It involves computing complex nonlinear wave-body interactions, hence taxing heavily computational resources. Here, we put forward a new simulation paradigm by training recurrent type neural networks (RNNs) that take as input the stochastic wave elevation at a certain sea state and output the main vessel motions, e.g., pitch, heave and roll. We first compare the performance of standard RNNs versus GRU and LSTM neural networks (NNs) and show that LSTM NNs lead to the best performance. We then examine the testing error of two representative vessels, a catamaran in sea state 1 and a battleship in sea state 8. We demonstrate that good accuracy is achieved for both cases in predicting the vessel motions for unseen wave elevations. We train the NNs with expensive CFD simulations offline, but upon training, the prediction of the vessel dynamics online can be obtained at a fraction of a second. This work is motivated by the universal approximation theorem for functionals [1], and it is the first implementation of such theory to realistic engineering problems.

Highly-scalable, physics-informed GANs for learning solutions of stochastic PDEs

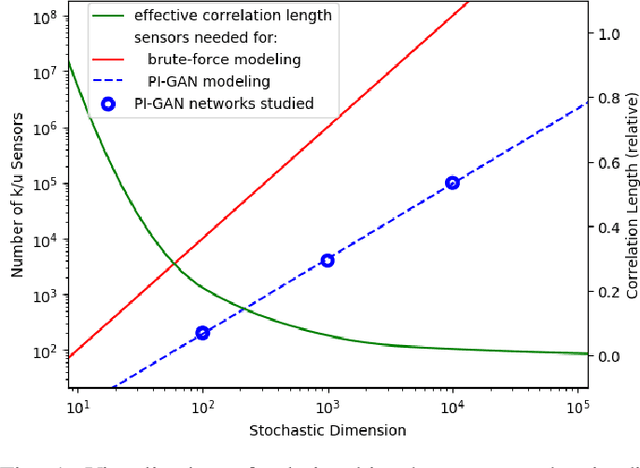
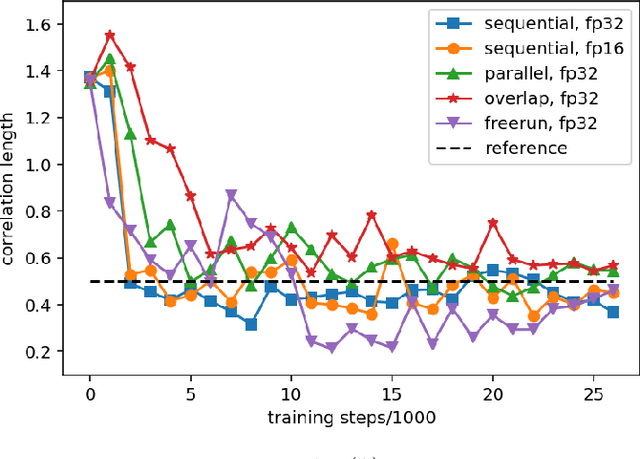
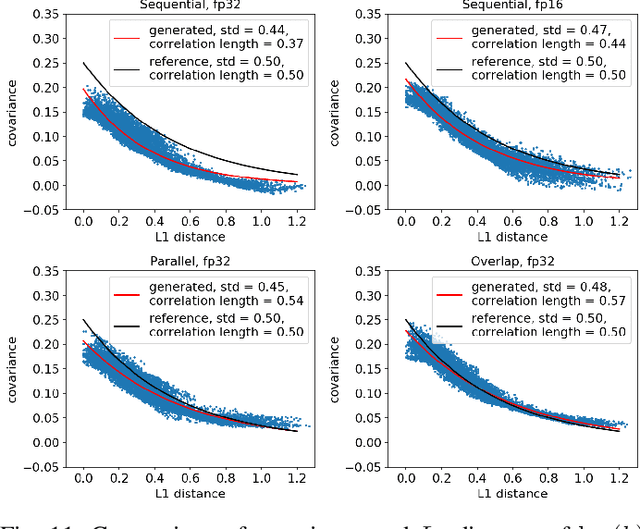
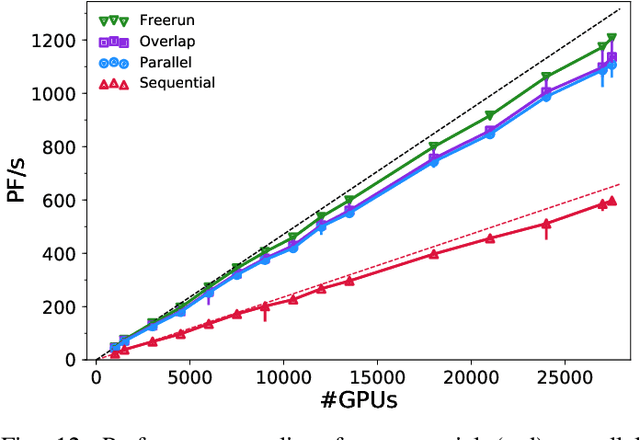
Uncertainty quantification for forward and inverse problems is a central challenge across physical and biomedical disciplines. We address this challenge for the problem of modeling subsurface flow at the Hanford Site by combining stochastic computational models with observational data using physics-informed GAN models. The geographic extent, spatial heterogeneity, and multiple correlation length scales of the Hanford Site require training a computationally intensive GAN model to thousands of dimensions. We develop a hierarchical scheme for exploiting domain parallelism, map discriminators and generators to multiple GPUs, and employ efficient communication schemes to ensure training stability and convergence. We developed a highly optimized implementation of this scheme that scales to 27,500 NVIDIA Volta GPUs and 4584 nodes on the Summit supercomputer with a 93.1% scaling efficiency, achieving peak and sustained half-precision rates of 1228 PF/s and 1207 PF/s.

Machine Learning of Space-Fractional Differential Equations

Data-driven discovery of "hidden physics" -- i.e., machine learning of differential equation models underlying observed data -- has recently been approached by embedding the discovery problem into a Gaussian Process regression of spatial data, treating and discovering unknown equation parameters as hyperparameters of a modified "physics informed" Gaussian Process kernel. This kernel includes the parametrized differential operators applied to a prior covariance kernel. We extend this framework to linear space-fractional differential equations. The methodology is compatible with a wide variety of fractional operators in $\mathbb{R}^d$ and stationary covariance kernels, including the Matern class, and can optimize the Matern parameter during training. We provide a user-friendly and feasible way to perform fractional derivatives of kernels, via a unified set of d-dimensional Fourier integral formulas amenable to generalized Gauss-Laguerre quadrature. The implementation of fractional derivatives has several benefits. First, it allows for discovering fractional-order PDEs for systems characterized by heavy tails or anomalous diffusion, bypassing the analytical difficulty of fractional calculus. Data sets exhibiting such features are of increasing prevalence in physical and financial domains. Second, a single fractional-order archetype allows for a derivative of arbitrary order to be learned, with the order itself being a parameter in the regression. This is advantageous even when used for discovering integer-order equations; the user is not required to assume a "dictionary" of derivatives of various orders, and directly controls the parsimony of the models being discovered. We illustrate on several examples, including fractional-order interpolation of advection-diffusion and modeling relative stock performance in the S&P 500 with alpha-stable motion via a fractional diffusion equation.

Deep Multi-fidelity Gaussian Processes

We develop a novel multi-fidelity framework that goes far beyond the classical AR(1) Co-kriging scheme of Kennedy and O'Hagan (2000). Our method can handle general discontinuous cross-correlations among systems with different levels of fidelity. A combination of multi-fidelity Gaussian Processes (AR(1) Co-kriging) and deep neural networks enables us to construct a method that is immune to discontinuities. We demonstrate the effectiveness of the new technology using standard benchmark problems designed to resemble the outputs of complicated high- and low-fidelity codes.